2.1 What Is Statistical Learning?
- 광고와 특정 상품의 판매량을 분석해 TV, 라디오, 신문 각각의 광고 횟수에 따른 상품 판매량을 정확하게 예측해야 하는 업무를 해야 한다고 하자.
즉, 3개의 매체에 대한 광고 횟수에 기반한 상품 판매량을 정확하게 예측하는 모델을 개발해야 한다. - 이 때 각각의 광고 횟수는 predictor, 종속 변수(independent variable), feature 또는 변수라고 부른다. -> X
이에 따른 상품 판매량은 response 또는 dependent variable이다. -> Y
이 관계를 수식으로 일반화해서 표현하면 다음과 같다 :
Y = f(X) + epsilon
여기서 epsilon 값은 랜덤한 오차를 의미한다.
본질적으로, Statistical Learning은 f를 추정하기 위한 일련의 접근 방식을 의미한다.
f를 추정하는 주요한 이유는 예측과 추론 두가지이다.
Prediction
대부분의 문제에서 input X는 이미 준비되었거나 얻기 쉽지만, output Y는 그렇지 않다. 이런 상황에서 오차가 0으로 수렴할 때 Y를 실제 값이 아니더라도 실제 f에 근사한 f를 통해 근사치를 얻을 수 있다.
Y에 대한 예측은 reducible error와 irreducible error에 따라 정확성을 판단할 수 있다.
일반적으로 f-근사는 f에 대한 정확한 추정이 아니기 때문에 이러한 비정확성은 오차를 발생시킨다. 이런 오차는 f를 추정하는 다양한 통계적 학습 기술을 사용해 더 정확하게 f를 근사함으로서 줄일 수 있다.
irreducible error
하지만, f에 대해 완벽한 추정을 수행해 f-근사 = f라고 해도 Y에 대한 예측은 여전히 오차를 지닐 수 있다. 왜냐하면 Y를 예측하는 것에는 입실론 값도 영향을 끼치기 때문이다. X만으로는 예측할 수 없다. 즉 입실론과 관련된 가변성 또한 예측에 영향을 가한다. 이런 오차를 irreducible error라고 하며, 얼마나 f를 잘 추정하던지와 상관없이, 입실론 값에 의해 발생하는 오차는 줄일 수 없다.
irreducible error가 존재할 수 밖에 없는 이유는 입실론 값이 f를 추정하는 데 사용되지 않은 Y를 예측하는데 유용한 변수들을(때론 측정할 수도 없는) 함축하고 있을 것이기 때문이다.
f-근사와 X를 고정하는 것을 가정했을 때, 가변성은 입실론 값에서만 기인한다.
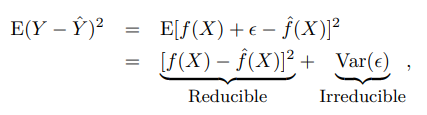
좌항이 실제 Y값과 예측된 값의 오차 제곱의 평균 또는 예측값을 표현할 때, Var(입실론)은 입실론 오차에 따른 분산을 표현한다.
우리가 할 일을 f를 추정해 reducible error를 줄이는 것이지만, Y에 대한 예측을 수행할 때 irreducible error가 상한선을 만든다는 것을 항상 기억해야 한다.
설명력
model이 black box가 아니라 설명 가능해야 한다면 어떤 점들을 고려해야 할까?
대표적으로 아래와 같은 점들을 고려할 수 있다:
- 어떤 X가 Y와 연관되어 있는가?
- 각각의 X와 Y의 관계는 어떤 관계인가?
- 관계가 선형방정식으로 표현할 수 있는가? 그렇지 않다면 더 복잡한 관계인가?
model의 설명력이 중요하지 않은 경우도 있고 매우 중요한 경우도 있다. 각각의 feature들과 Y의 관계를 설명하는 것에 크게 관심이 없다면 model이 blackbox여도 무관하다. 하지만 관계성이 중요할 경우(inference paradigm)에는 설명가능한 모델을 사용하거나 시각화할 수 있어야 한다.
2.1.2 How do we estimate f?
f를 추정하는 여러 선형적이거나 비선형적인 방법론이 있지만 이들은 일반적으로 특정한 성질을 공유하고 있다.
우리의 목표는 주어진 training data를 이용해서 모든 경우의 (X , Y) 쌍에 대해 Y를 근사하게 예측하는 f를 추정하는 것이다. 모수적(parametric) 방법론이든 비모수적(non-parametric) 방법론이든 이 목적으로 특정할 수 있다.
Parametric Methods
Parametric Method는 크게 두 단계로 나누어 접근한다.
첫번째로, f의 functional form or shape을 추정하는 것이다.
대표적으로 f를 X를 입력으로 하는 선형적인 함수로 가정한 후 추정하는 방법론이 있다. 이러한 가정을 하고 나면 f를 추정하는 문제는 무척 간단해진다.
두번째로, 위처럼 모델을 선택했다면 training data를 이용해 모델을 훈련하는 과정이 필요하다.
이런 모델 기반 접근법을 Parametric하다고 하며, f를 추정하는 문제를 파라미터들을 추정하는 문제로 단순화한다. 임의의 함수 f를 학습시키는 것이다.
Parametric Methods는 선택한 모델이 알 수 없는 실제 f와 맞지 않을 수 있다는 잠재적인 위험성을 가지고 있다. 만약 선택한 모델이 실제 f와 크게 차이가 난다면 모델의 성능은 현저히 떨어질 것이다.
그래서 우리는 flexible한 모델을 이용해 다양한 functional form을 적용할 수 있다. 그러나 flexible한 모델은 일반적으로 더 많은 parameter를 사용하는데 이는 모델이 training data에 overfitting되는 것을 초래할 수 있다.
Non-parametric Methods
Non-parametric methods는 함수를 추정하는 방법론을 사용하지 않는다. 대신 기존에 알고 있는 데이터 포인트들을 통해 y를 추정한다. 즉 새로운 함수나 판단 알고리즘을 만드는 것이 아니라 데이터 의존적인 방법론이다.
이 방법은 하나의 추정 함수를 사용하는 것으로 귀결해 잘못 추정된 모델을 사용하면 결과가 수렴하지 못할 수 있는 Parametric methods에 비해 학습된 파라미터가 아니라 데이터에 의존해 판단해 위와 같은 위험성이 없다.
하지만 f를 추정하는 문제를 파라미터를 추정하는 문제로 단순화하지 못했기 때문에 정확한 추정을 위해서는 많은 수의 데이터를 필요로 한다.
ex ) k n-neighbor, k n-cluster
The Trade-off Between Prediction Accuracy And Model Interpretability
위에 나온 model의 설명력과 연관되어 있는 지점이다. Parametric methods를 사용할 때 일반적으로 간단한 모델보다는 flexible한 모델을 사용해야 예측의 정확도가 높아진다고 했다. flexible한 모델은 사용하는 파라미터의 수가 많은데, 당연히 모델의 설명력은 떨어지게 될 것이다. DNN을 이용해서 판매량을 예측하는 문제를 해결한다고 했을 때, 각 파라미터가 어떤 것을 의미하는지 아는 것은 사실상 불가능하다.
하지만 설명력보다 예측의 정확도와 성능을 중시한다면 flexible한 모델을 선택하는 것이 합리적일 것이다.
반대로 설명할 수 있는지의 여부가 중요하다면 설명할 수 있지만 비교적 flexible하지 않은 모델을 사용하는 것이 좋을 것이다.
Supervised Versus Unsupervised Learning
지도학습 : 모델이 예측해야 하는 y 값이 training data에 주어져 있어 학습 과정에서 이를 예측하고 오차를 계산하는 방식으로 최적화를 진행한다. 대부분의 고전적 / 최신 모델이 지도학습 방식을 따른다.
비지도학습 : 지도학습과 다르게 y 값이 주어지지 않고 training data에 주어진 x set만 있을 경우에 사용한다. data point 사이의 관계나 feature 사이의 관계를 통해 clustering을 하거나 이상치를 검출하는데 많이 사용된다.
대부분의 문제가 지도학습과 비지도학습으로 구분될 수 있지만, 어떤 경우에는 확고히 구분하기 어렵다. 예를 들어 데이터의 일부는 y 값을 가지고 있지만 나머지는 그렇지 않은 경우, 준지도학습을 이용해 y값이 없는 데이터도 이용해 학습할 수 있다.
Regression versus Classification
변수들은 양적인(quantitative) 것과 질적인(qualitative) 것(categorical)으로 나눌 수 있다. 양적인 것은 숫자로 표현하고 (즉 연속적이다), 질적인 변수(categorical)는 n개의 class로 표현하거나 카테고리로 표현한다 (즉 비연속적이다).
회귀 : 지도학습 양적인 변수를 y 값으로 하는 문제를 말한다.
분류 : 지도학습에서 질적인 변수를 y 값으로 하는 문제를 말한다.
2.2 Assessing Model Accuracy
모든 케이스에 전부 최고의 성능을 내는 모델은 없을까? 하나의 특정한 케이스에 하나의 모델이 최고의 성능을 낼 수는 있지만, 비슷하지만 다른 케이스에는 다른 모델이 더 적합할 수 있다. 주어진 케이스에 대해서 어떤 모델이 최고의 성능을 낼지 결정하는 것이 무척 중요하다.
정리해서 말하자면, 각각의 문제에는 각자의 최고의 모델이 있다.
2.2.1 Measuring the Quality of Fit
통계적 학습의 성능을 평가하기 위해서는 예측한 값이 실제 정답과 일치하는지 비교해야 한다. 학습 과정에서 우리는 데이터셋에 있는 실제 정답과 예측한 정답과의 오차를 계산하며 파라미터를 업데이트하며 학습하지만, 실제로 중요한 것은 훈련 데이터에서의 오차가 아니라 우리가 알 수 없는 unseen data에서의 generalization이다.
그렇기 때문에 train set에서의 오차가 가장 작은 모델을 선택하는 것이 아니라 test data (unseen data의 일부)에서의 오차가 가장 작은 모델을 선택해야 한다.
train set에서의 오차는 작지만, test data에서의 오차가 큰 경우 Overfitting이라고 한다. 위에서 말한대로 파라미터의 수가 많은 flexible model의 경우 train set에 과도하게 학습되어 일어난다.
2.2.2 Bias-Variance Trade-off
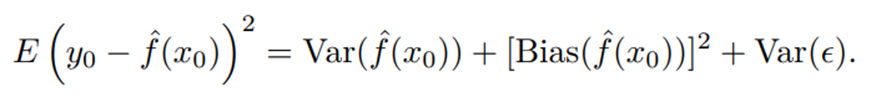
bias는 모델이 예측한 값과 실제 값의 편차를 의미한다.
variance는 모델이 서로 다른 sample data에 대해 예측한 값들 사이의 편차, 말 그대로 분산이다.
좋은 모델은 bias와 variance의 합을 낮추는 최적점을 찾아야 한다.
bias를 낮춰야 한다는 점은 자명하다. bias가 높다는 모델이 Underfitting되어 있다는 것이다.
variance가 높다는 건 어떤 것을 의미할까? 위의 Overfitting이 일어나는 모델이 variance가 높은 모델이다. training data에 맞춰져 있는 함수 모델이기 때문에 서로 다른 값들 사이의 편차가 클 것이다. 즉 일반화 성능을 측정하는 지표이다.
문제는 bias와 variance 사이의 trade-off 관계이다.
bias를 최대한 낮추기 위해 모델을 훈련하면 training data에 과대적합되어 variance는 올라갈 것이다.
반대로 variance를 최대한 낮추기 위해 훈련하면 올바른 예측이 불가능해 bias가 올라갈 것이다.
bias와 variance의 교차점이 바로 모델의 최적점일 가능성이 크다.
Classification Setting
현재까지 본 개념들은 회귀 문제를 기준으로 서술되었다. Bias-variance Trade-off와 같은 개념들은 분류 문제에서는 다르게 정의될 수 있다.
분류 문제에서는 평가지표를 회귀문제에서의 MSE처럼 예측값과 실제값 사이의 차를 이용하지 않고 예측한 카테고리와 실제 카테고리가 일치하는지 아닌지를 기준으로 측정한다.
