💡 Contains Duplicate

여러번 나오는 숫자 찾는 문제이다

Solution

std::unordered_set<>

store unique elements in no particular order, but organize into buckets
which bucket an element is placed into depends on the hash of its value
once a hash is computed, it refers to the exact bucket

allow for fast retrieval

elements are keys, they are immuntable but can be inserted and deleted

search, insertion, removal have average contstant-time complexity
서로 다른 key값이라도 hash function에 의해 변환된 index 값이 같을 수 도 있음
그래서 각각의 bucket은 linked list로 구현

faster than set to access individual elements by their key

/*
	Time: O(n)
    Space: O(n)
*/
    
class Solution {
public:
    bool containsDuplicate(vector<int>& nums) {
        unordered_set<int> s;

        for (int i = 0; i < nums.size(); i++) {
            if (s.find(nums[i]) != s.end()) return true; //find is O(1)
            s.insert(nums[i]);
        }

        return false;
    }
};

---

💡 Valid Anagram

Given two strings s and t, return true if t is an anagram of s, and false otherwise.

An Anagram is a word or phrase formed by rearranging the letters of a different word or phrase, typically using all the original letters exactly once.

Example 1:

Input: s = "anagram", t = "nagaram"
Output: true

Example 2:

Input: s = "rat", t = "car"
Output: false

Constraints:

• 1 <= s.length, t.length <= 5 * 104
• s and t consist of lowercase English letters.

Solution

class Solution {
public:
    bool isAnagram(string s, string t) {
        if (s.size() != t.size()) return false;

        vector<int> alphabet(26);

        for (int i = 0; i < s.size(); i++) {
            alphabet[s[i] - 'a']++;
        }

        for (int i = 0; i < t.size(); i++) {
            alphabet[t[i] - 'a']--;
            if (alphabet[t[i] - 'a'] < 0) {
                // when the alphabet count becomes negative,
                //  no further computation is needed 
                return false;
            }
        }

        return true;

    }
};

---

💡 Two Sum

Given an array of integers nums and an integer target, return indices of the two numbers such that they add up to target.

You may assume that each input would have exactly one solution, and you may not use the same element twice.

You can return the answer in any order.

Example 1:

Input: nums = [2,7,11,15], target = 9
Output: [0,1]
Explanation: Because nums[0] + nums[1] == 9, we return [0, 1].

Example 2:

Input: nums = [3,2,4], target = 6
Output: [1,2]

Example 3:

Input: nums = [3,3], target = 6
Output: [0,1]

Constraints:

• 2 <= nums.length <= 104
• 109 <= nums[i] <= 109
• 109 <= target <= 109
• Only one valid answer exists.

Solution

std::unordered_map<>

using hash table, the search is O(1)

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        vector<int> result;
        
        // store nums[i] as key
        // and the index as value
        unordered_map<int, int> m;

        for (int i = 0; i < nums.size(); i++) { //O(n)
            int complement = target - nums[i];
            if (m.find(complement) == m.end()) { //O(1)
                m.insert({nums[i], i});
            } else {
                result.push_back(i);
                result.push_back(m[complement]);
                break;
            }
        } //O(n)

        return result;

    }
};

---

💡 Group Anagrams

Given an array of strings strs, group the anagrams together. You can return the answer in any order.

An Anagram is a word or phrase formed by rearranging the letters of a different word or phrase, typically using all the original letters exactly once.

Example 1:

Input: strs = ["eat","tea","tan","ate","nat","bat"]
Output: [["bat"],["nat","tan"],["ate","eat","tea"]]

Example 2:

Input: strs = [""]
Output: [[""]]

Example 3:

Input: strs = ["a"]
Output: [["a"]]

Constraints:

• 1 <= strs.length <= 104
• 0 <= strs[i].length <= 100
• strs[i] consists of lowercase English letters.

Solution

class Solution {
public:
    vector<vector<string>> groupAnagrams(vector<string>& strs) {
        // key is sorted string
        // value is anagrams
        unordered_map<string, vector<string>> group_anagrams;

        for (string s : strs) { //O(n)
            string original = s;
            sort(s.begin(), s.end()); //O(m logm) 
            if (group_anagrams.find(s) != group_anagrams.end()) { //O(1)
                group_anagrams[s].push_back(original);
            } else {
                vector<string> anagrams;
                anagrams.push_back(original);
                group_anagrams.insert({s, anagrams});
            }
        } //O(nm logm)
        
        vector<vector<string>> result;
        for (auto it = group_anagrams.begin(); it != group_anagrams.end(); ++it) { //O(n)
            result.push_back(it->second);
        }

        return result;

    }
};

sort의 시간 복잡도는 O(m logm)이다 (m은 string.size())
string을 sort하는 시간 복잡도를 O(m)으로 만들 순 없을까?
→ 알파벳을 세는 저장소를 따로 만든다면 가능하다!

class Solution {
public:
    vector<vector<string>> groupAnagrams(vector<string>& strs) {
        // key is sorted string
        // value is anagrams
        unordered_map<string, vector<string>> group_anagrams;

        for (string s : strs) { //O(n)
            string sorted = mySort(s); //O(m)
            if (group_anagrams.find(sorted) != group_anagrams.end()) { //O(1)
                group_anagrams[sorted].push_back(s);
            } else {
                vector<string> anagrams;
                anagrams.push_back(s);
                group_anagrams.insert({sorted, anagrams});
            }
        } //O(nm)

        vector<vector<string>> result;
        for (auto it = group_anagrams.begin(); it != group_anagrams.end(); ++it) { //O(n)
            result.push_back(it->second);
        }

        return result;

    }

private: 
    string mySort(string str) { //O(m)
        vector<int> alphabet_count(26);

        for (int i = 0; i < str.size(); i++) {
            alphabet_count[str[i] - 'a']++;
        }

        string sorted = "";
        for (int i = 0; i < 26; i++) {
            string add_string = string(alphabet_count[i], i + 'a');
            sorted.append(add_string);
        }

        return sorted;
    }
};

근데,,

이렇게 열심히 바꿔놨는데 정작 첫번째 solution이 더 효율적이라고 뜨네,,? (왜지

이게 첫번째,,

그리고 이게 두번쨰,,

흠 ,, 대체 왜 !!!

---

💡 Top K Frequent Elements

Given an integer array nums and an integer k, return the k most frequent elements. You may return the answer in any order.

Example 1:

Input: nums = [1,1,1,2,2,3], k = 2
Output: [1,2]

Example 2:

Input: nums = [1], k = 1
Output: [1]

Constraints:

• 1 <= nums.length <= 105
• 104 <= nums[i] <= 104
• k is in the range [1, the number of unique elements in the array].
• It is guaranteed that the answer is unique.

Follow up: Your algorithm's time complexity must be better than O(n log n), where n is the array's size.

Solution

풀이를 간단히 그림으로 그려보자면 이렇다

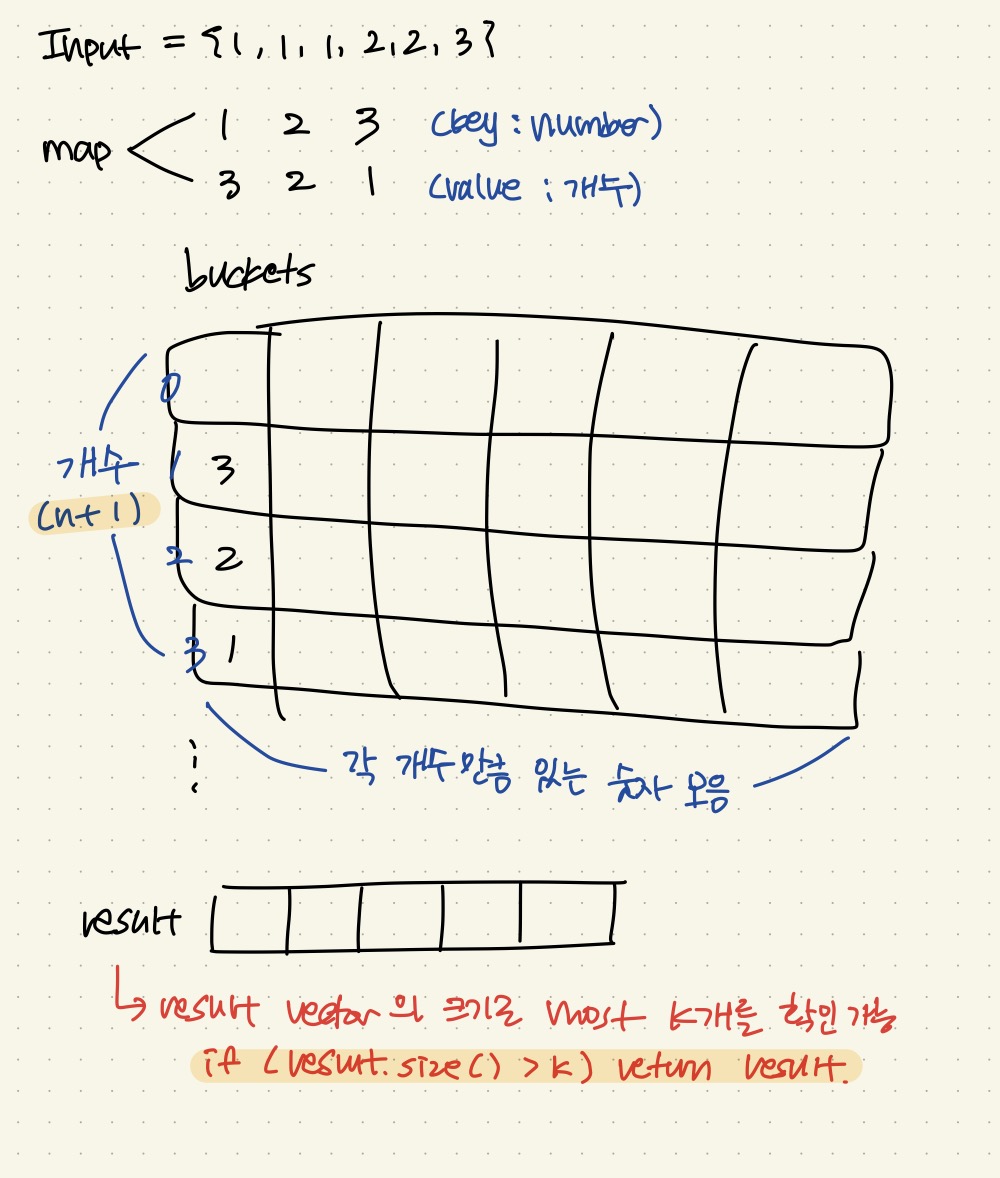
unordered_map을 이용해서 숫자과 그 숫자가 몇개있는지를 기록해준다

2D int vector (bucket)을 사용하여
bucket의 index는 숫자의 개수들을 나타낸다
이 때 index는 최대 n+1개이다 (n은 input nums의 element개수)

각 index의 vector에는 그 개수만큼 있는 숫자를 push_back해준다

이 작업까지 완료가 되면 result 벡터를 만드는데,
이때 result의 크기로 'the most k'개를 간단히 확인 할 수 있다.

class Solution {
public:
    vector<int> topKFrequent(vector<int>& nums, int k) {
        int size = nums.size();

        unordered_map<int, int> m;
        for (int i = 0; i < size; i++) {
            m[nums[i]]++;
        }

        vector<vector<int>> bucket(size + 1);
        //iterate over the map (m)
        for (auto it = m.begin(); it != m.end(); ++it) {
            bucket[it->second].push_back(it->first);
        }

        vector<int> result;
        for (int i = size; i > 0; i--) {
            if (result.size() >= k) {
                // break, not return
                // because the control may not reach here 
                //  :when k > # unique elements in nums
                break;
            }

            while (!bucket[i].empty()) {
                result.push_back(bucket[i].back());
                bucket[i].pop_back();
            }

        }

        return result;
    }
};

---

💡 Product of Array Except Self

Given an integer array nums, return an array answer such that answer[i] is equal to the product of all the elements of nums except nums[i].

The product of any prefix or suffix of nums is guaranteed to fit in a 32-bit integer.

You must write an algorithm that runs in O(n) time and without using the division operation.

Example 1:

Input: nums = [1,2,3,4]
Output: [24,12,8,6]

Example 2:

Input: nums = [-1,1,0,-3,3]
Output: [0,0,9,0,0]

Constraints:

• 2 <= nums.length <= 105
• -30 <= nums[i] <= 30
• The product of any prefix or suffix of nums is guaranteed to fit in a 32-bit integer.

Follow up: Can you solve the problem in O(1) extra space complexity? (The output array does not count as extra space for space complexity analysis.)

Solution

읭 이거 그냥 다 애초에 한번에 곱해놓고 다시 나누면 되는거 아닌가
이렇게 간단하다고?

아 근데 이건 0이 하나 껴있으면 안되는구나,,
0을 어떻게 처리하지.. 흠

flag를 써야할 것 같은데
.. 이렇게 해도 time comlexity와 auxiliary space는 지켜지지만,,,
too many edge cases!

컨디션에 영향을 받지 않는 방법은:

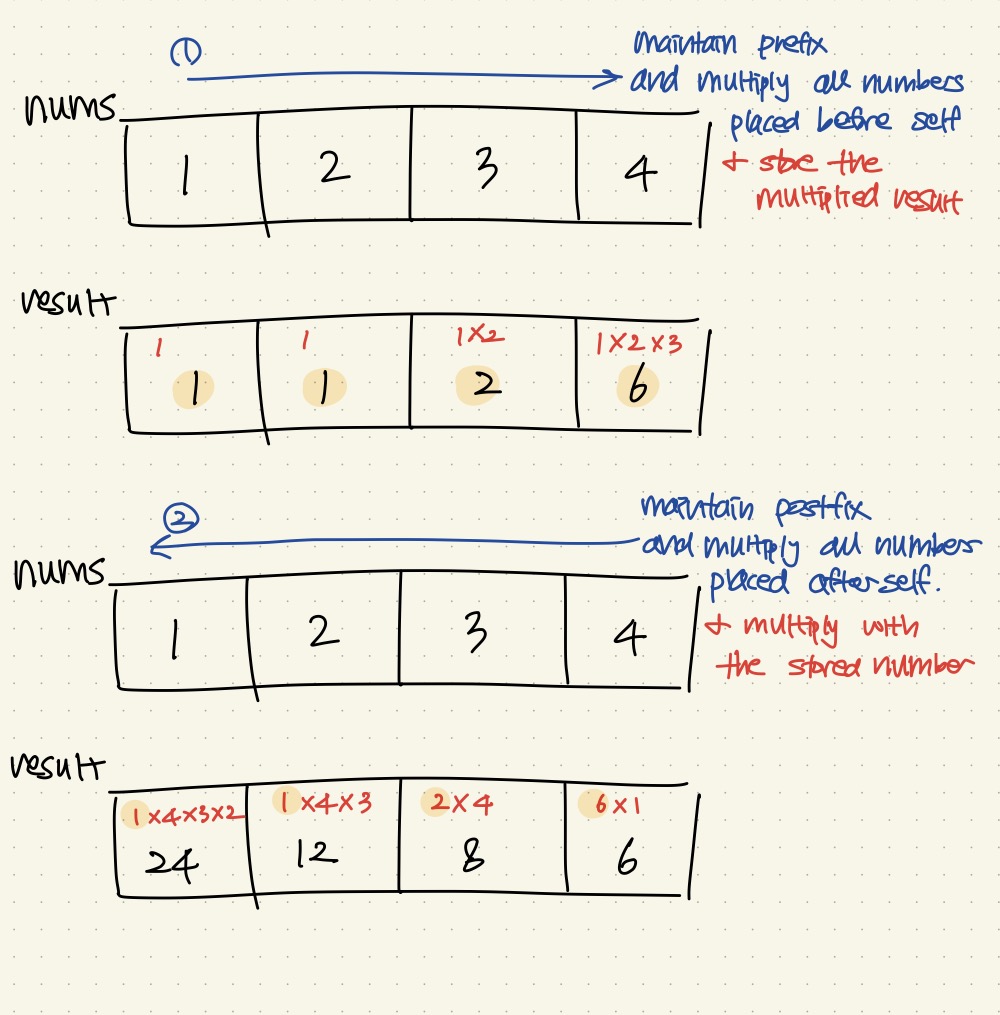
class Solution {
public:
    vector<int> productExceptSelf(vector<int>& nums) {
        int n = nums.size();
        vector<int> result(n, 1);

        int prefix = 1;
        for (int i = 0; i < nums.size(); i++) {
            result[i] = prefix;
            prefix *= nums[i];
        }
       
        int postfix = 1;
        for (int i = n-1; i >= 0; i--) {
            result[i] *= postfix;
            postfix *= nums[i];            
        }

        return result;
    }
};

간단하구만!

---

💡 Encode and Decode Strings

머여 이 문제는 또 유료네 ㅡ,.ㅡ

comment로 달려있는 걸로 문제를 예상해보면
Design algorithm to encode/decode: list of strings <-> string

그냥 머 ,, encode하고
그걸 어떻게 다시 원상복구하느냐가 핵심문제인 것 같고만

Solution

class Codec {
public:

    // Encodes a list of strings to a single string.
    string encode(vector<string>& strs) {
        string result = "";
        
        for (int i = 0; i < strs.size(); i++) {
            string str = strs[i];
            result += to_string(str.size()) + "#" + str;
        }
        
        return result;
    }

    // Decodes a single string to a list of strings.
    vector<string> decode(string s) {
        vector<string> result;
        
        int i = 0;
        while (i < s.size()) {
            int j = i;
            while (s[j] != '#') {
                j++;
            }
            int length = stoi(s.substr(i, j - i));
            string str = s.substr(j + 1, length);
            result.push_back(str);
            i = j + 1 + length;
        }
        
        return result;
    }
private:
};

// Your Codec object will be instantiated and called as such:
// Codec codec;
// codec.decode(codec.encode(strs));

간단스하네!

---

💡 Longest consecutive Sequence

Given an unsorted array of integers nums, return the length of the longest consecutive elements sequence.

You must write an algorithm that runs in O(n) time.

Example 1:

Input: nums = [100,4,200,1,3,2]
Output: 4
Explanation: The longest consecutive elements sequence is [1, 2, 3, 4]. 
Therefore its length is 4.

Example 2:

Input: nums = [0,3,7,2,5,8,4,6,0,1]
Output: 9

Constraints:

• 0 <= nums.length <= 105
• 109 <= nums[i] <= 109

Solution

class Solution {
public:
    int longestConsecutive(vector<int>& nums) {
        //turn into hash set for constant time retreival
        unordered_set<int>s(nums.begin(), nums.end());
        int longest = 0; //return value

        for (auto &n : s) { //O(n)
            //when this number is the start of the sequence
            if (s.count(n - 1) == 0) { 
                int length = 1;
                while (s.count(n + length)) {
                    length += 1;
                }
                longest = max(longest, length);
            }
        }

        return longest;

    }
};

looks like quadratic due to the while loop nested within the for loop
but the while loop is actually linear

왜냐면,,

while loop is only reached when the current number is the start of a sequence (check it with s.count(
the while loop can only run for n iterations throughout the entire runtime

---

💡 Valid Sudoku

check if the filled cells are valid

Solution

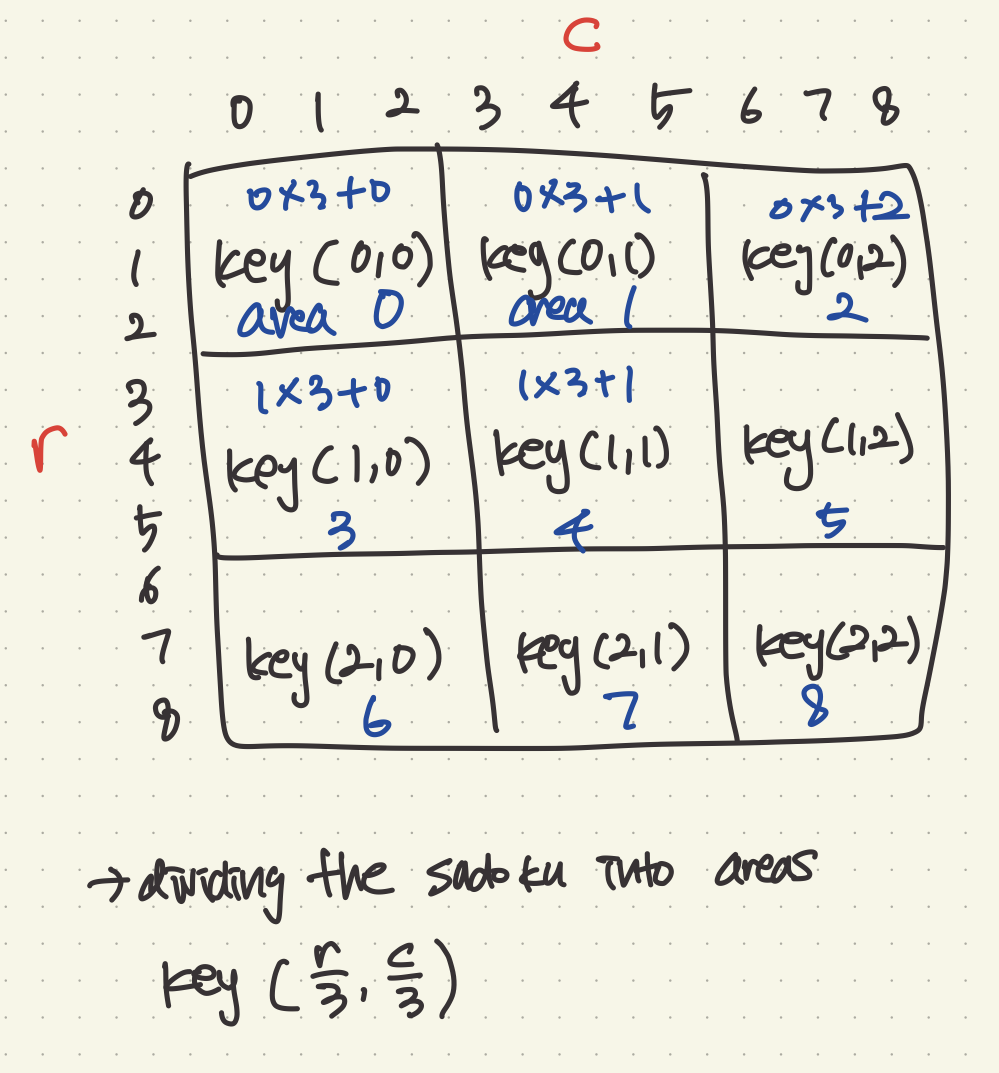
class Solution {
public:
    bool isValidSudoku(vector<vector<char>>& board) {
        const int n = 9;
        bool row[n][n] = {false}; // if seen number 5 in row #1, then mark row[1][5] = true
        bool col[n][n] = {false}; 
        bool sub[n][n] = {false}; // it seen number 5 in area #1, then mark sub[1][5] = true;

        for (int r = 0; r < n; r++) {
            for (int c = 0; c < n; c++) {
                if (board[r][c] == '.')
                    continue;
                
                int number = board[r][c] - '0' - 1;
                int area = (r/3) * 3 + (c/3);

                if (row[r][number] || // if seen this number in current row
                    col[c][number] || // if seen this number in current col
                    sub[area][number]) { 
                    return false;
                }

                // mark seen number
                row[r][number] = true;
                col[c][number] = true;
                sub[area][number] = true;
            }
        }

        return true;

    }
};