TIL (2022.04.20)

Pascal's Triangle From LeetCode

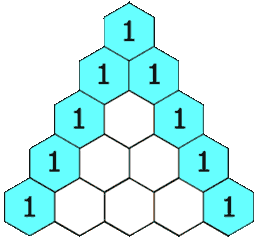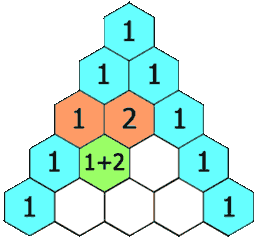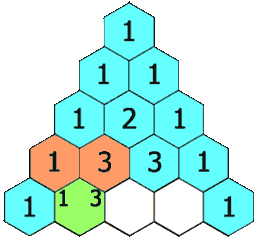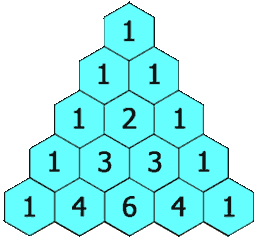
Pascal's triangle works like this.

예시를 보면,
Input: numRows = 5
Output: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]

즉 1로 시작해서 1로 끝나고 그 사이에 값들이 들어가면 된다.
내가 i=3번째 줄의 j=2번째 자리의 값을 넣어야 한다면,

[i-1][j-1]+[i-1][j]
즉, 2번째 줄의 1번 값과 2번값을 넣어주면 되는 것이다.

i=4번째 줄의 j=3번이라면?
[3][2]+[3][3]을 넣어주면 되겠다.

이를 구현해보자.

class Solution {
public:
    vector<vector<int>> generate(int numRows) {
        vector<vector<int>> tri(numRows);
        // 제일 상단의 값은 고정
        tri[0].push_back(1);
        
        for(int i=1;i<numRows;i++){
        // 한 줄의 첫번째 값은 1으로 고정 
            tri[i].push_back(1);
            for(int j=1;j<i;j++){
            // 우리가 찾은 점화식 
                tri[i].push_back(tri[i-1][j-1]+tri[i-1][j]);
            }
            // 한 줄의 마지막 값은 1으로 고정
            tri[i].push_back(1);
        }
        return tri;
    }
};

11047번 동전 0
K원을 만드는데 필요한 동전 개수의 최솟값을 출력하기

예제 입력은
N개의 동전가치 / K원
10 4200
1
5
10
50
100
500
1000
5000
10000
50000

출력은

6

일단 벡터에 값들을 입력받고, 그 이후에 거꾸로 내려가면서 풀어줬다. 4200/50000을 해보고 0보다 큰 경우만 체크해줌
예를 들어 4200/1000이면 4가 나오니까
4200 - (4200/1000 * 1000) 해서 값 변경

다음으로 넘어가기.

#include <iostream>
#include <vector>
using namespace std;

int main(){
    int n,k;
    cin>>n>>k;

    vector<int> coins;

    for(int i=0;i<n;i++){
        int coin;
        cin>>coin;
        coins.push_back(coin);
    }

    int count = 0;
    for(int i=coins.size()-1;i>=0;i--){
        if(k/coins[i]>0){
            count+=(k/coins[i]);
            k=k-((k/coins[i])*coins[i]);
        }
    }

    cout<<count;
}