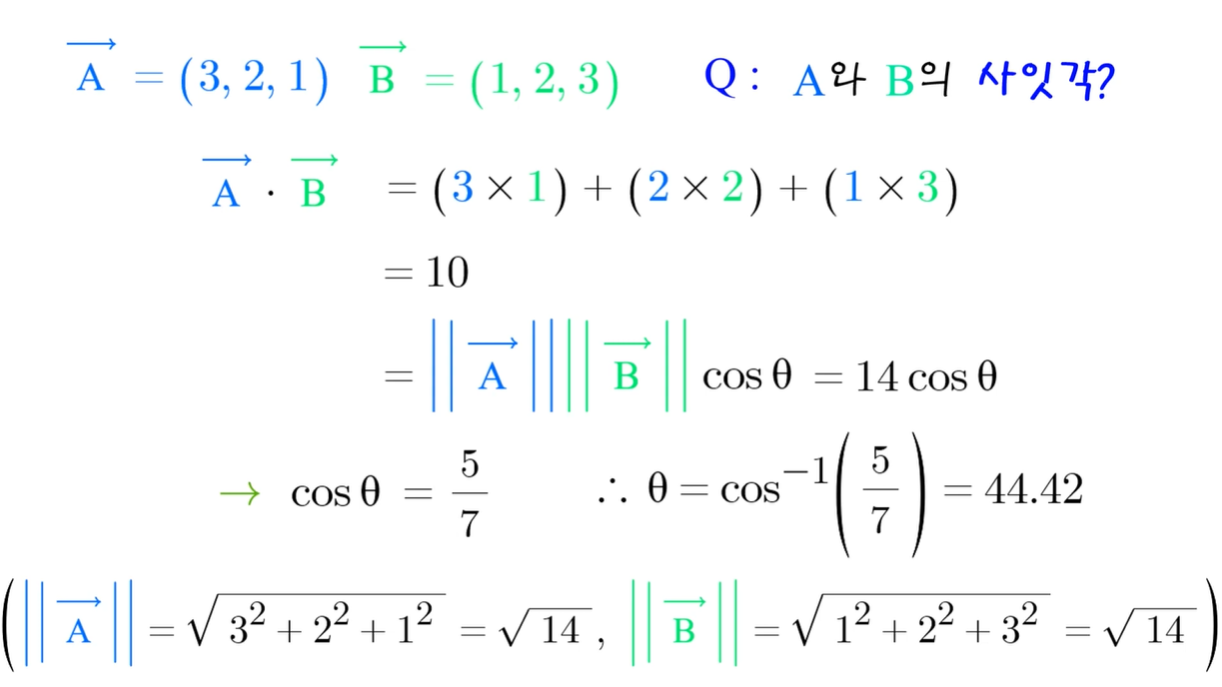A. sine(사인), cosine(코사인), tangent(탄젠트)
1. sine(사인) : sin
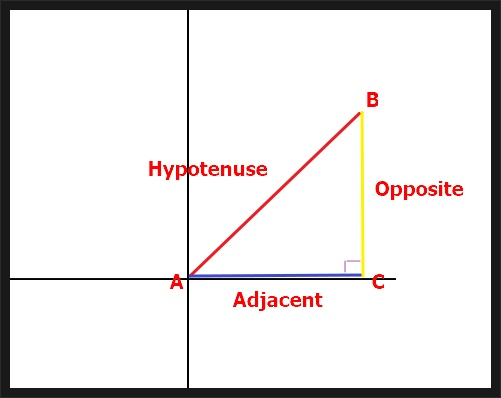
- sinθ(사인 세타) 는 직삼각형의 임의의 각도가 θ 일때, Hypotenuse(빗변)과 Opposite(높이)의 비율
- sinθ = Opposite(높이) / Hypotenuse(빗변) => 빗변 분의 높이
2. cosine(코사인) : cos
- cosθ(코사인 세타) 는 직삼각형의 임의의 각도가 θ 일때, Hypotenuse(빗변)과 Adjacent(밑변)의 비율
- cosθ = Adjacent(밑변) / Hypotenuse(빗변) => 빗변 분의 밑변
3. tangent(탄젠트)은 tan
- tanθ(탄젠트 세타) 는 직삼각형의 임의의 각도가 θ 일때, Adjacent(밑변)과 Opposite(높이)의 비율
- tanθ = Opposite(높이) / Adjacent(밑변) => 밑변 분의 높이
B. 벡터의 내적과 외적 기본 계산 공식
- 내적 구하는 방법
- 외적 구하는 방법
- 헷갈리면 x y z가 있을 때, x는 1열 지우고 크로스 계산, y는 2열 지우고 크로스 계산, z는 3열 지우고 크로스 계산으로 생각하면 된다.
- 예제 ) A = 4i - 5j - 6k, B = i + 2j - 3k 두 벡터의 내적과 외적을 구하시오.(i, j, k는 x,y,z 축의 단위벡터. i = (1,0,0) )▶내적: x,y,z 좌표끼리 곱하기만 하면 되므로,
→ 4x1 + (-5 ) x 2 + (-6) x (-3) = 4 - 10 + 18 = 12
▶외적: 위 공식에 따라 계산해준다.
→ x좌표 : 15 + 12 = 27
→ y좌표 : -6 + 12 = 6
→ z좌표 : 8 + 5 = 13
즉 AxB = (27, 6, 13)
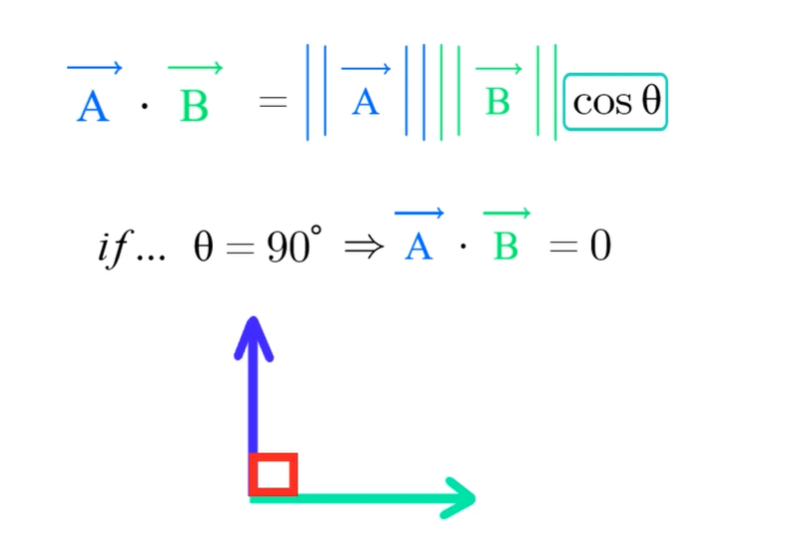
C. cosθ 90도인 경우 내적은 0 이다.
- 그러므로,
-> cosθ 값이 양수 : 90도보다 작거나 270도보다 클 때
-> cosθ 값이 음수 : 90도보다 크고, 270도보다 작을때
-> cosθ 값이 0 : 90도 또는 270도