float과 double에 관심을 기울인적 있는가?
float과 double은 우리가 프로그래밍을 배우면서 정말 바로 나오는 애들 중 하나이다.
그냥 있는거고 원래 있었던 애들.. 회사에서도 사실 잘 사용하지 않아왔었는데 문득 이런 생각이 들었다
도대체 왜 만들었지? 🤔
사실 프로그래밍 공부를 하면서 점점 중요하다가 느끼는 것 중 하나가 '호기심을 잃지 않는 것이다' 처음에 공부를 시작할때는 모든 것이 새로웠고 신기했기에 어디에나 호기심이 가득한 상태로 공부해왔다. 그러나, 시간이 지나고 직장 생활을 하다보니 기존에 존재를 알고 있던 것을 정말 깊숙히 알고 있는 것으로 착각하고, 어렵고 신기한것만 탐구하려는 성향이 강해짐을 느껴진다. 이번에 float과 double에 대해 공부하면서 이런 기초적인 것에도 많은 것이 담겨있는데 난 이제까지 알고 있다고 착각하고 있었구나 라는 것을 느낀다.
자, 본격적으로 이제 내가 공부한 내용을 차근차근 읊어볼까~?
Float과 Double 차이점에 대해 알고 있어?
float과 double은 모두 숫자를 저장하기 위한 기본 자료형이다.
float은 32비트의 저장소로 소수점 이하 약 7자리의 정확도를 가지고 있고, double은 64비트의 저장소로 소수점 이하 약 15자리의 정확도를 가진다.
여기서 우리가 주목해야 할 점은
- 정확도에 차이가 있다.
-> double이 float보다 정확도가 높구나? - 메모리에 차이가 있다
-> float이 double의 절반의 메모리를 사용한다. 따라서 메모리 효율성이 float이 더 높다. 그럼 double보다 더 많은 데이터를 다룰 수 있다는 것이고 연산속도도 더 빠르겠네~! - 부동소수점을 위한 기본 자료형이 float과 double이다.
부동소수점?
- 실수를 표현하는 방식 중 하나
- 숫자를 지수와 가수로 나누어 저장하여 소수점의 위치가 자유롭게 변할 수 있는 방식
"부동"은 "떠다니다" 라는 의미로, 소수점의 위치가 고정되어 있지 않고 숫자의 크기에 따라 위치가 변할 수 있음을 나타낸다.그래서 부동소수점은 매우 큰 수나 작은 수를 지수의 크기에 따라 동적으로 표현 할 수 있다. 즉, 넓은 수자 범위를 효율적으로 표현할 수 있다는 것
-> 모든 실수를 정확하게 표현 할 수 없다
부동소수점의 한계 예시
난 이거 알아볼때 사실 감동이었다.ㅎㅎ
1) 0.1
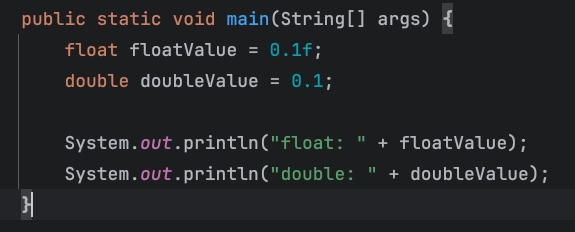
( 아, 이건 번외인데 +라는 기호는 쓰지말자..ㅎ)
단순히 작동하면 출력 결과가
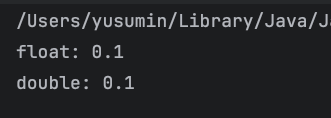
0.1로 나온다. 그럼 정확한거잖아?? 라고 생각할 수 있다. 하지만 이는 반올림의 결과이다 실제로 내부의 값을 bigDecimal을 이용해 확인해보면

결과는? 두둥

정확히 0.1이 아님을 알 수 있다.
2) 0.2와 0.1의 덧셈
부동소수점의 정밀도로 인해 기대값이 0.3이 아닐 수 있다.
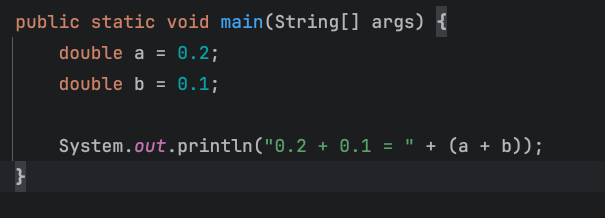
의 결과는?

정확히 0.3이 안나오는데 정확성이 중요한 곳에서는 어떻게 부동소수점을 쓰겠는가?
그럼 정확성이 중요할 때는 뭘 사용해야하지?
BigDecimal을 사용해야한다.
BigDecimal
위의 덧셈 연산을 그대로 bigDecimal을 적용해보자면
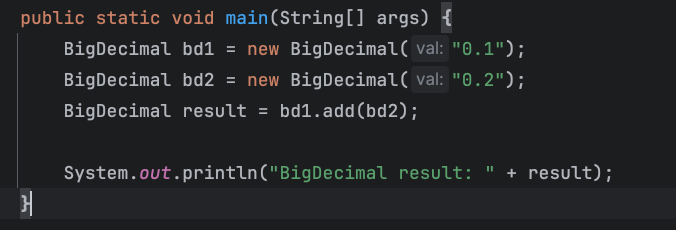
의 결과는

으로 정확한 숫자가 나오는 것을 확인할 수 있다. 그래서 정확도가 필요한 상황이라면 BigDecimal을 사용해야한다. 하지만 단점도 존재한다.
- 연산 속도가 float, double보다 느리다.
- 메모리 사용량이 높다
- 성능 저하
BigDecimal은 참조형이다. 즉 매번 덧셈, 곱셈, 나눗셈과 같은 기본 연산에서도 객체를 생성해야한다. 객체를 새로 생성한다는 말은 즉, 메모리를 추가로 사용한다는 말이다. 이는 곧 숫자의 크기가 커질 수록 더많은 연산 자원을 소모해서 성능 저하를 발생시킬 가능성이 있다는 말이다.
선택 정리
- 느리지만 높은 정확도가 필요하다면?
BigDecimal - 높은 정밀도는 필요하지 않지만 많은 소수점 연산을 빠르게 처리해야하거나 메모리 효율이 중요한 경우?
float - float보다는 정밀도가 높고 성능 저하가 없으며 메모리에 대한 여유가 있으면?
Double
