JavaScript에서 0.1 + 0.2 를 출력해보면 0.3이 아닌 다른 결과를 얻게 됩니다.
let num1 = 0.1;
let num2 = 0.2;
let sum = num1 + num2;
console.log(sum); // 0.30000000000000004
파이썬도 같은 결과가 나옵니다. 마찬가지로 Java, C에서도 같은 결과가 나옵니다.

0.1 + 0.2 = 0.3 이라는 것은 초등학생도 알고있을텐데 왜 저런 결과가 나올까요?
위의 결과를 이해하기 위해서는 컴퓨터에서의 숫자 표현 방식에 대해 이해하고 있어야 합니다.
부동소수점 형식
JavaScript에서는 숫자를 표현하기 위해 IEEE 754 배정밀도 부동 소수점 형식(Double-precision floating-point format)을 사용합니다. (참고로 C언어에서는 float 는 단정밀도(32bit), double 은 배정밀도(64bit) 형식을 사용합니다.)
해당 방식은 64bit를 사용하여 숫자를 표현하고, 비트는 다음과 같이 배치됩니다.
- 부호 비트(Sign bit) : 1bit
- 지수(Exponent) : 11bit
- 유효 정밀도(Significand precision) : 52bit

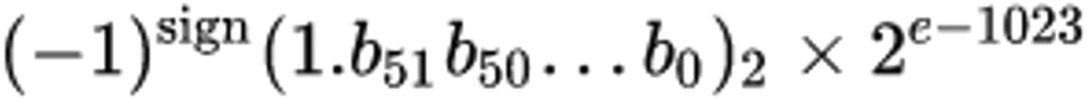
지수 표현하면 다음과 같습니다.
그럼 배정밀도 부동 소수점 형식에서는 어떤식으로 숫자를 표현하는지 예시를 들어 보겠습니다.
먼저 0.25 라는 실수를 이진수로 표현하면 0.01 입니다.
이 숫자를 정규화를 하게되면 1.0 * 2^-2 로 표현할 수 있고, 부동 소수점 형식을 활용해 표현하면 다음과 같습니다.
- 부호비트 : 0
- 지수 : 01111111101
- 유효정밀도 : 10000000…
// 배정밀도 부동 소수점 형식에서 표현한 0.25
0 01111111101 1000000000000000000000000000000000000000000000000000정밀도 손실(loss of precision)
그래서 0.1 + 0.2은 왜 0.3이 안되는 걸까요?
우선 0.1을 이진수로 표현해보면 다음과 같습니다.

0.00011001100110011001100110011001100110011001100…0.1을 이진수로 표현하면 0.0001100 뒤에 1100이 계속 반복되는 구조입니다. 다만 부동소수점 방식에서는 정밀도 표현 비트가 한계가 있기 때문에(배정밀도 방식에서는 53bit) 정확히 표현할 수 없습니다.
그래서 IEEE-754에선 가능한 가장 가까운 숫자로 반올림 하는 방법을 표현해 이런 문제를 해결합니다.
다만 연산 과정에서 두 숫자를 합하게 되면 정밀도 손실도 더해지게 됩니다.
문제를 해결하기 위해서는 JavaScript에서 toFixed(n) 메소드를 활용할 수 있습니다. 다만 해당 메소드는 문자열을 반환하기 때문에 숫자형으로 변환하기 위해 단항 덧셈 연산자를 활용하면 됩니다.
let num1 = 0.1;
let num2 = 0.2;
let sum = num1 + num2;
console.log(sum.toFixed(2)); // 0.30
console.log(+sum.toFixed(2)); // 0.3
