기초수학 w/python

---

1. 팩토리얼

📁 Python 활용법

#for문

input_n = int(input('n입력 : '))

result = 1
for i in range (1,input_n +1):
    result *= i

print(f'{input_n}팩토리얼 : {result}')

#while문

n = 1
result = 1
while n <= input_n :
    result *= n
    n += 1

print(f'{input_n}팩토리얼 : {result}')

#재귀함수

def factorialFun(n) :
    if n == 1 : return 1

    return n * factorialFun(n-1)

print('{}팩토리얼 : {}'.format(input_n,factorialFun(input_n)))

---

2. 군수열

📋 이론

군으로 묶은 항의 개수 1,2,3,4,5를 등차수열로 본다면,
군의 개수의 합이 항의 순서가 된다.
e.g. 5번째 군까지의 합은 = 15 => 항 15번째가 5군 마지막

군수열을 공식을 대입하면
an = n
sn = (n^2 +n)/2가 되고,
임의의 값 9를 넣었을 때 값이 45이므로
9군까지 45번째 항이 오고 50번째 항은 10군의 다섯번째인 5가 오게된다.

📁 Python 활용법

input_n = int(input('n항 입력 :'))

flag = True
n=1 ; cnt = 1; result = 0

while flag :

    #군
    for i in range(1,(n+1)):
        print(f'{i}\t',end='')
        
        #항 수 적립
        cnt +=1

        if (cnt > input_n) :
            result = i
            flag = False
            break

    print()
    n += 1

print(f'{input_n}항 : {result}')

---

3. 순열

순서와 상관있이 n개에서 r개를 택하여 나열하는 경우의수
순서가 다르면 다른 경우의 수로 본다.
nPr = n! / (n-r)!

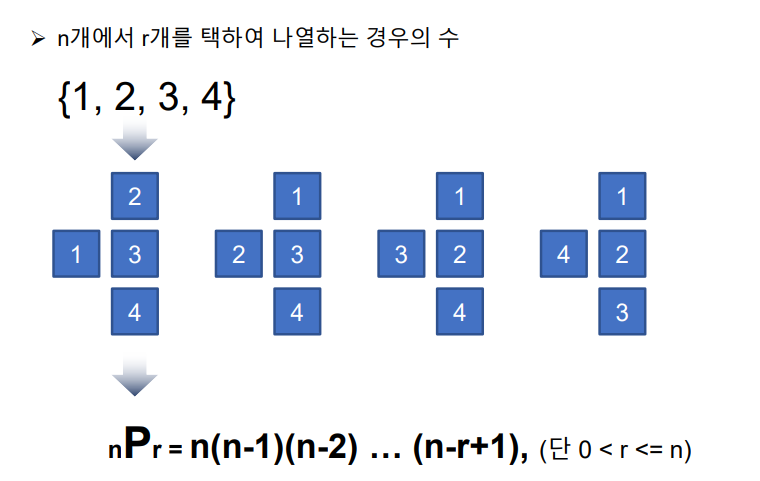
e.g. 2,1 != 1,2

📋 팩토리얼과의 관계

두가지 계산식 암기필수!

📁 Python 활용법

#공식 1
#n(n-1)(n-2)..(n-r+1)

num_n = int(input('num_n 입력 : '))
num_r = int(input('num_r 입력 : '))

result = 1
for n in range (num_n,(num_n-num_r),-1) :
    result *= n

print(result)

#공식 2
#n!/(n-r)!

num_n = int(input('num_n 입력 : '))
num_r = int(input('num_r 입력 : '))

up = 1
down = 1

for i in range (1,num_n +1) :
    up *= i

for i in range (1,(num_n-num_r)+1):
    down *= i

result = int(up / down)
print(result)

➕원순열

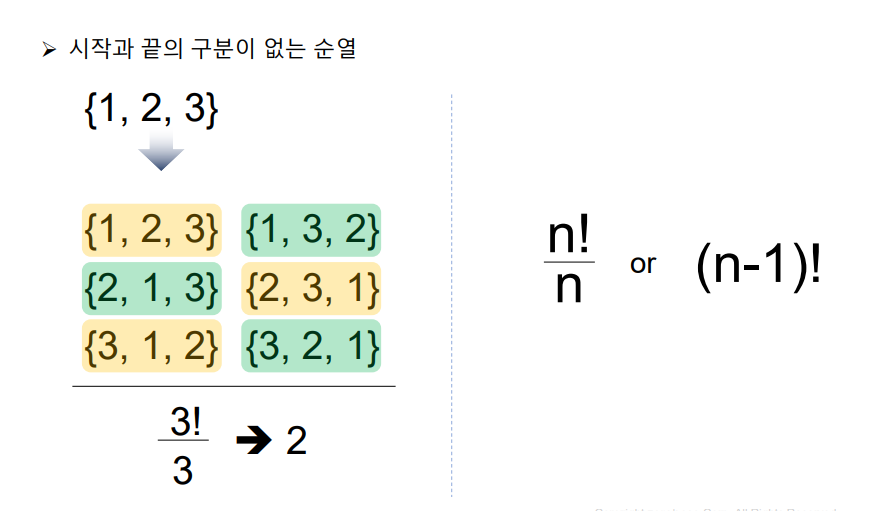
순서가 달라도 같은 경우의 수
e.g. {1,2,3} = {2,3,1} = {3,1,2}

공식 암기할것

• (n-1)!
• n! /n

#실습 : 4명의 친구가 원탁 테이블에 앉을 수 있는 순서를 계산해보자
#n!/n or (n-1)!

#(n-1)!
n = int(input('친구 수 입력 : '))
result = 1
for i in range(1,n) :
    result *= i

print(result)

# n!/n
result2 = math.factorial(n) // n
print(result2)

---

4. 조합

순서와 상관있이 n개에서 r개를 택하여 나열
순서가 달라도 같은 경우의 수로 본다.
nCr = nPr / r! = n! / r!(n-r)!

num_n = int(input('num_n값 입력 : '))
num_r = int(input('num_r값 입력 : '))
result_n = 1
result_r = 1
result = 1

#nPr = n * (n-r+1)
for n in range(num_n,(num_n-num_r),-1) :
    result_n *= n

print(result_n)

#r!
for i in range(num_r,0,-1) :
    result_r *= i

print(result_r)

result = int(result_n/result_r)

print(result)

---

5. 확률

모든사건에서 특정사건이 일어날 수 있는 수를 나타낸것

• 모든사건 : 표본공간(sample)
• 특정사건 : 사건(event)

#박스에 꽝이 적힌 종이가 4장, 선물이 적힌 종이가 3장있을때
#꽝 2장과 선물 1장을 뽑는 확률

#모든사건 : 7장에서 3장을 뽑을 때 7C3

#사건1 [꽝 2장] : 4장의 꽝에서 2장을 뽑을 때 4C2
#사건2 [선물 1장] : 3장의 꽝에서 1장을 뽑을 때 3C1

#즉, 4C2 * 3C1 / 7C3

#nCr 함수

def ncr_function() :
    num_n = int(input('num_n 입력 : '))
    num_r = int(input('num_n 입력 : '))

    result1 = 1
    result2 = 1
    result3 = 1

    #nPr
    for i in range(num_n,(num_n-num_r),-1) :
        result1 *= i

    #r!
    for i in range(num_r,0,-1) :
        result2 *= i

    #nPr / r!
    result3 = result1/result2

    return result3

sample = ncr_function()
event1 = ncr_function()
event2 = ncr_function()

probability = (event1 * event2)/sample
print('probability : {}%'.format(probability*100))

---

제로베이스 데이터취업스쿨

Daily Study Note