DFS와 BFS
DFS와 BFS는 그래프의 각 정점을 방문하는 그래프 순회(Graph Traversals) 알고리즘이다. 미로찾기를 위해 처음 고안된 DFS는 주로 스택과 재귀로 구현하며 일반적으로 BFS에 비해 널리 쓰인다. BFS는 주로 큐로 구현하며 최단 경로를 구하는 경우에 주로 사용된다.
DFS와 BFS 구현의 핵심은 한 번 방문한 곳은 다시 방문하지 않는다는 점이다.
다음과 같은 순회 그래프가 있다고 하자.
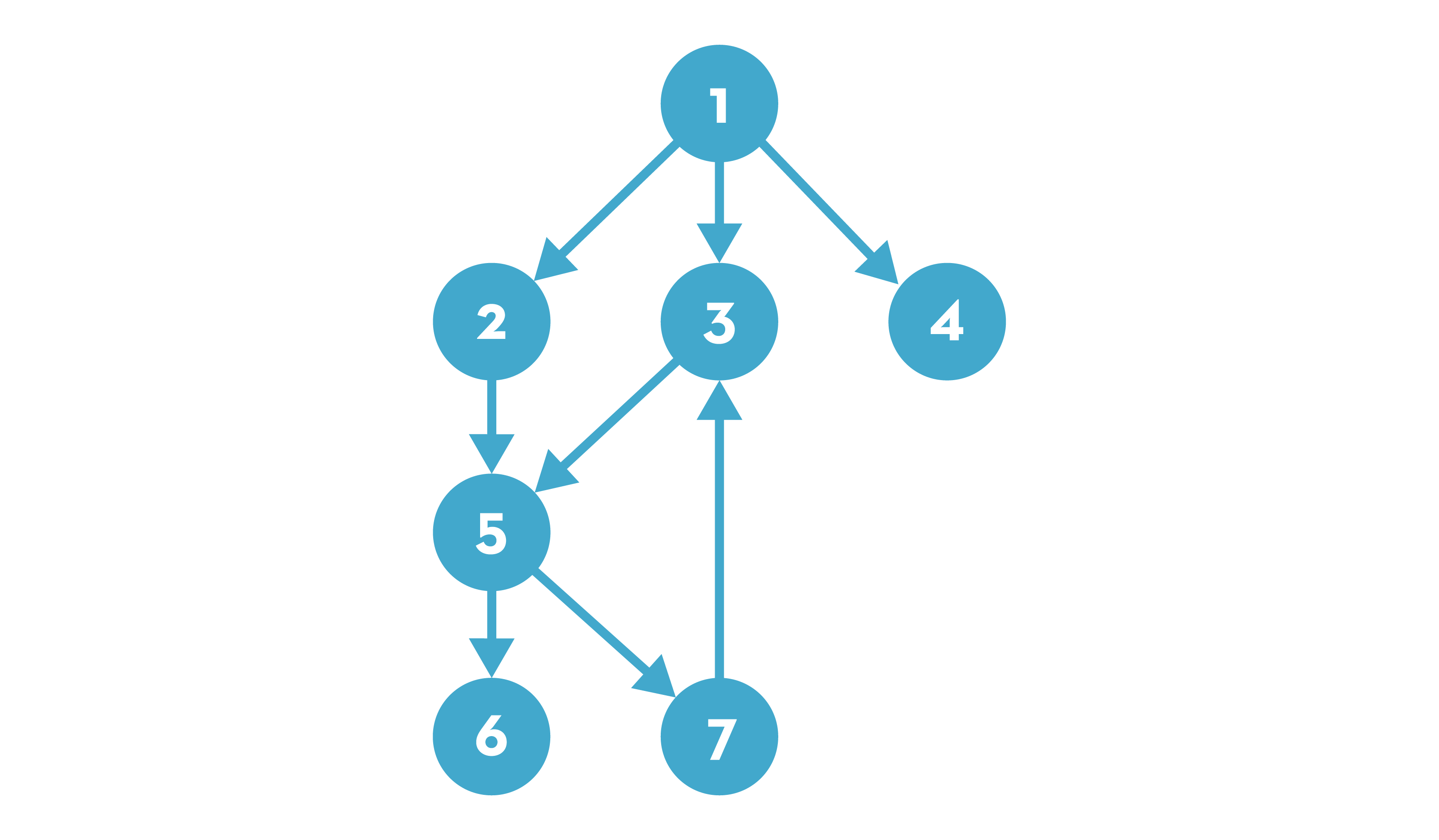
이를 딕셔너리(객체) 인접 리스트로 표현하면 다음과 같다.
graph = {
1: [2, 3, 4],
2: [5],
3: [5],
4: [],
5: [6, 7],
6: [],
7: [3],
}다음은 각 알고리즘을 직접 구현하는 코드이다.
DFS
DFS는 재귀와 스택 두 가지 방법으로 구현할 수 있다.
재귀를 이용한 구현
파이썬
def recursive_dfs(v, discovered=[]):
discovered.append(v)
for w in graph[v]:
if w not in discovered:
discovered = recursive_dfs(w, discovered)
return discovered
graph = {
1: [2, 3, 4],
2: [5],
3: [5],
4: [],
5: [6, 7],
6: [],
7: [3],
}
recursive_dfs(1) # [1, 2, 5, 6, 7, 3, 4]자바스크립트
function recursiveDfs(v, discovered = []) {
discovered.push(v);
for (let w of graph[v]) {
if (!discovered.includes(w)) {
discovered = recursiveDfs(w, discovered);
}
}
return discovered;
}
graph = {
1: [2, 3, 4],
2: [5],
3: [5],
4: [],
5: [6, 7],
6: [],
7: [3],
}
recursiveDfs(1); // [1, 2, 5, 6, 7, 3, 4]| w | discovered |
|---|---|
| 2 | [1] |
| 5 | [1, 2] |
| 6 | [1, 2, 5] |
| 7 | [1, 2, 5, 6] |
| 3 | [1, 2, 5, 6, 7] |
| 4 | [1, 2, 5, 6, 7, 3] |
스택을 이용한 구현
파이썬
def stack_dfs(start_v):
discovered = []
stack = [start_v]
while stack:
v = stack.pop()
if v not in discovered:
discovered.append(v)
for w in graph[v]:
stack.append(w)
return discovered
graph = {
1: [2, 3, 4],
2: [5],
3: [5],
4: [],
5: [6, 7],
6: [],
7: [3],
}
stack_dfs(1) # [1, 4, 3, 5, 7, 6, 2]자바스크립트
function stackDfs(startV) {
let discovered = [];
let stack = [startV];
while (stack.length > 0) {
let v = stack.pop();
if (!discovered.includes(v)) {
discovered.push(v);
for (let w of graph[v]) {
stack.push(w);
}
}
}
return discovered;
}
graph = {
1: [2, 3, 4],
2: [5],
3: [5],
4: [],
5: [6, 7],
6: [],
7: [3],
}
stackDfs(1); // [1, 4, 3, 5, 7, 6, 2]| v | stack | discovered |
|---|---|---|
| - | [1] | [] |
| 1 | [2, 3, 4] | [1] |
| 4 | [2, 3] | [1, 4] |
| 3 | [2, 5] | [1, 4, 3] |
| 5 | [2, 6, 7] | [1, 4, 3, 5] |
| 7 | [2, 6, 3] | [1, 4, 3, 5, 7] |
| 3 | [2, 6] | [1, 4, 3, 5, 7] |
| 6 | [2] | [1, 4, 3, 5, 7, 6] |
| 2 | [5] | [1, 4, 3, 5, 7, 6, 2] |
스택을 이용한 방식은 재귀를 이용한 방법의 역순으로 가장 마지막인 4 부터 3, 5... 순으로 방문한다. 두 방식의 순서는 다르지만 결과적으로 모두 DFS를 구현한 것을 볼 수 있다.
BFS
BFS는 큐를 이용하여 구현할 수 있으나 재귀를 이용해서 구현하는 것은 불가능하다!
큐를 이용한 구현
파이썬
def queue_bfs(start_v):
discovered = [start_v]
queue = [start_v]
while queue:
v = queue.pop(0)
for w in graph[v]:
if w not in discovered:
discovered.append(w)
queue.append(w)
return discovered
graph = {
1: [2, 3, 4],
2: [5],
3: [5],
4: [],
5: [6, 7],
6: [],
7: [3],
}
queue_bfs(1) # [1, 2, 3, 4, 5, 6, 7]자바스크립트
function queueBfs(startV) {
let discovered = [startV];
let queue = [startV];
while (queue.length > 0) {
let v = queue.pop(0);
for (let w of graph[v]) {
if (!discovered.includes(w)) {
discovered.push(w);
queue.push(w);
}
}
}
return discovered;
}
graph = {
1: [2, 3, 4],
2: [5],
3: [5],
4: [],
5: [6, 7],
6: [],
7: [3],
}
queueBfs(1); // [1, 2, 3, 4, 5, 6, 7]| v | queue | discovered |
|---|---|---|
| - | [1] | [1] |
| 1 | [2, 3, 4] | [1, 2, 3, 4] |
| 4 | [2, 3] | [1, 2, 3, 4] |
| 3 | [2, 5] | [1, 2, 3, 4, 5] |
| 5 | [2, 6, 7] | [1, 2, 3, 4, 5, 6, 7] |
참고
파이썬 알고리즘 인터뷰
