[알고리즘] 그래프 Graph

💡그래프란,

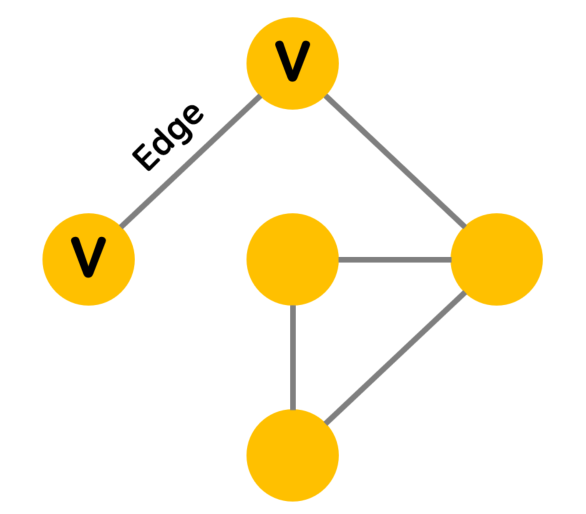
정점(Vertex)과 간선(Edge)으로 구성된 집합으로,
각 요소들 간의 연결 관계를 이진으로 표현하는 자료 구조이다.

📕그래프 용어

인접하다 Adjacent

두 정점을 잇는 간선이 존재할 때 두 정점은 인접한다라고 표현한다.

차수 Degree

한 정점과 인접한 정점의 수를 해당 정점에 대한 차수라고 한다.
방향 그래프의 경우 진입 차수와 진출 차수를 고려한다.

• 진입 차수 In-Degree: 정점으로 도착하는 간선의 수
• 진출 차수 Out-Degree: 정점에서 출발하는 간선의 수

📑그래프의 종류

그래프는 방향성과 순환성, 연결성, 간선의 특징에 따라 종류를 구분할 수 있다.

방향성에 따른 구분

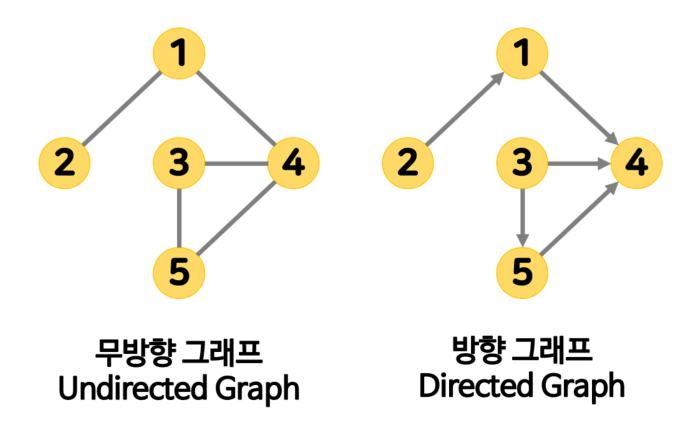
🔘 무방향 그래프 Undirected Graph

간선의 방향성이 없으며 간선으로 이어진 정점 간에는 양방향으로 이동할 수 있다. 따라서, $(1,2)$와 $(2,1)$은 동일한 간선이다.

🔘 방향 그래프 Directed Graph

간선이 방향성을 가져, 간선의 방향으로만 이동할 수 있다.

순환성에 따른 구분

🔘 순환 그래프 Cyclic Graph

경로의 시작 정점과 종료 정점이 동일하다. 이때 경로는 반복되는 정점이 없는 단순 경로(Simple Path)이다.

🔘 비순환 그래프 Acyclic Graph

시작 정점과 종료 정점이 동일하지 않는 순환이 없는 그래프이다.

연결성에 따른 구분

연결성에 따른 그래프는 방향성이 없는 무방향 그래프에서 구분된다.

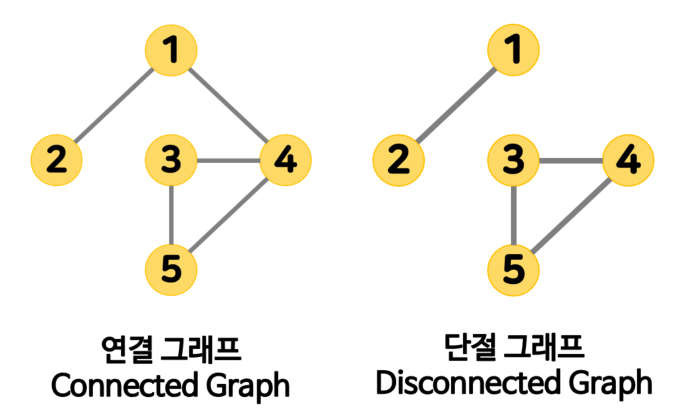
🔘 연결 그래프 Connected Graph

무방향 그래프 내 모든 정점 간의 경로가 존재한다.

🔘 단절 그래프 Disconnected Graph

무방향 그래프 내의 모든 정점 사이에 경로가 존재하지 않는다.

간선의 특징에 따른 구분

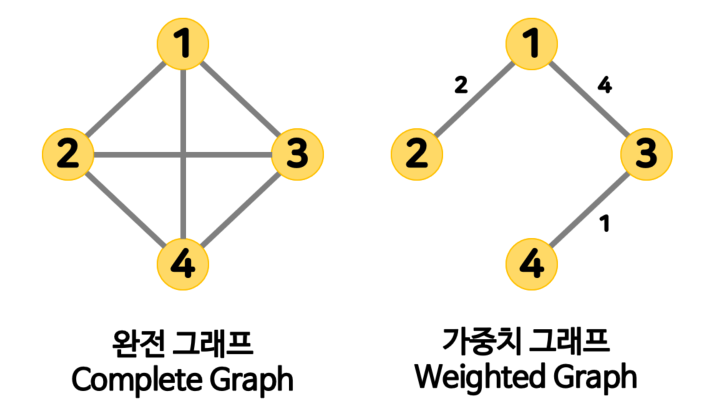
🔘 완전 그래프 Complete Graph

그래프 내 한 정점이 다른 정점과 모두 연결된 그래프로 최대 간선의 수를 가진다.

🔘 가중치 그래프 Weighted Graph

정점 사이를 연결하는 간선마다 가중치가 할당된 그래프이다. 정점 간에 이동할 때 비용이 발생한다고 이해하면 된다.

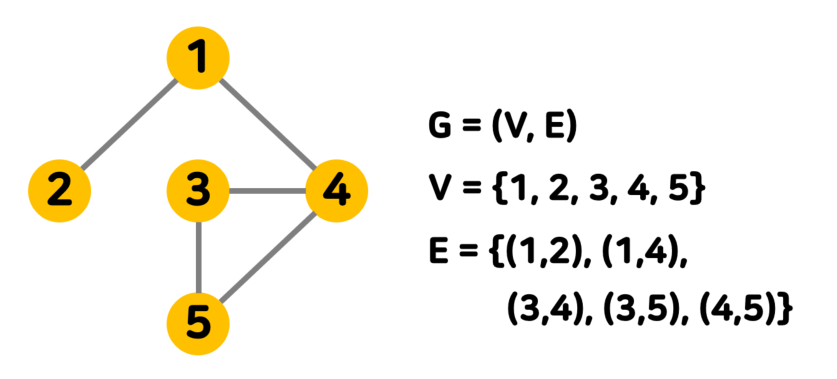
✏️그래프 표기법

그래프는 $G = (V, E)$로 표기하며 V는 정점의 집합, E는 간선의 집합이다.

⌨️그래프 구현방법

그래프는 파이썬에서 2가지 방법으로 구현할 수 있다.

1) 인접 행렬 Adjacency Matrix

인접 행렬을 구현하기 위해서는 정점의 개수가 $N$일 떄 $N \times N$ 행렬이 필요하다. 두 정점 $i$와 $j$ 간에 이동이 가능할 때 즉 간선이 존재할 때, $Matrix[i][j]$를 표시하는 방식으로 구현한다.

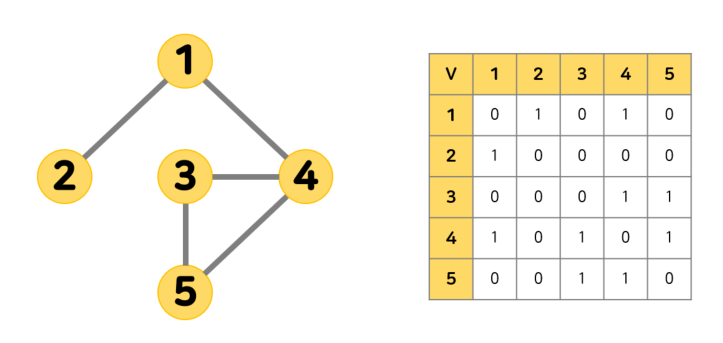
정리하자면, 인접 행렬은 간선이 있다면 1, 없다면 0으로 표현하는 불린 행렬(Boolean Matrix)이다.

그래서 구현이 아주 간단하다는 장점을 가지지만 정점의 개수가 많을 경우 메모리 소비가 크다는 단점이 있다. 또한 인접한 정점을 찾기 위해서는 모든 정점을 순회해야 한다는 가장 큰 단점이 있다.

2) 인접 리스트 Adjacency List

그래프를 구현하는 데 가장 일반적으로 사용되는 방식이다.
모든 정점을 해당 정점과 연결된 다른 정점들을 나열한 리스트로 표현하는 방법이다.

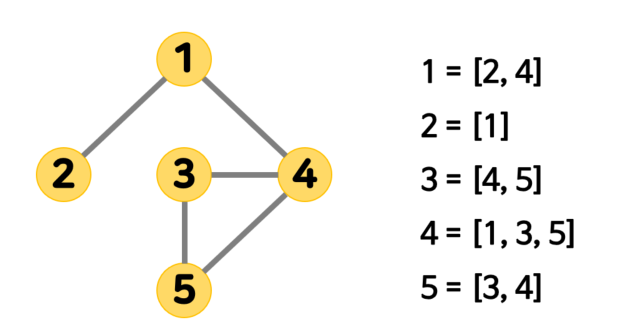
방향성은 출발 정점에만 정점을 추가하는 방식으로 표현할 수 있다. 그래서 무방향 그래프의 경우는 두 정점 리스트에 모두 추가하는 방식으로 구현된다.

인접 행렬에 비해 구현하는 방식이 다소 어렵지만 인접한 정점을 인덱스로 쉽게 접근할 수 있다는 장점을 가진다. 또한, 필요한 정보만을 저장하기 때문에 메모리 소비도 적다는 장점을 가진다.