1. Heaps
1) max heap / min heap의 세가지 성질
- 루트 노드는 항상 최댓값 또는 최솟값을 가짐
- Complete binary tree
- max(min) heap 내의 임의의 노드를 루트로 하는 서브 트리 또한 max(min) heap임
2) 이진 탐색 트리와 비교되는 heaps의 특징
- 원소들은 완전히 크기 순으로 정렬되어 있지 않음
- 특정 키 값을 가지는 원소를 빠르게 검색하기 어려움
- 완전 이진 트리여야 한다는 부가의 제약 조건을 갖고 있음
- 순회나 탐색 연산을 수행하기에 적절하지 않음
3) 배열을 이용한 이진 트리 표현
-
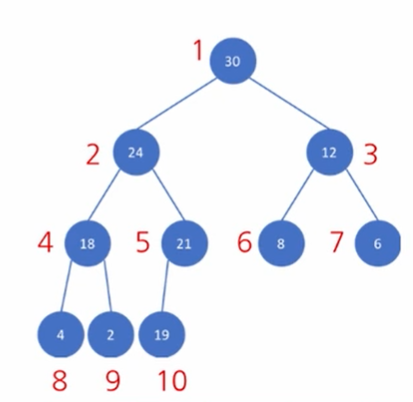
배열을 이용해서 이진 트리를 표현
-
노드 번호 m을 기준으로
- left child 번호 : 2 * m
- right child 번호 : 2 * m + 1
- parent node 번호 : m // 2
-
완전 이진 트리이기 때문에, 노드의 추가와 삭제는 마지막 노드에서만 일어남
2. heaps 구현
1) insert 메서드
- 트리의 마지막 자리에 새로운 원소를 임시 저장
- 부모 노드와 키 값을 계속 비교하면서 값이 더 크면 위로 이동시킴
- 원소의 개수가 n인 max heap에 새로운 원소 삽입
- 부모 노드와 대소 비교 최대 횟수 : log2n
- worse case에서의 복잡도 : O(logn)
class Maxheap:
def __init__(self): # empty heap 생성
self.data = [None]
def insert(self, item):
child = len(self.data) # 새로운 원소의 위치
parent = child // 2 # 새로운 원소의 부모 노드의 위치
self.data.append(item) # 마지막 자리에 새로운 원소 임시 저장
while child > 1:
if self.data[child] > self.data[parent]: # 부모 노드와 키 값을 비교
# 더 크면 부모 노드와 위치를 변경
self.data[child], self.data[parent] = self.data[parent], self.data[child]
else:
break
child = parent
parent = child // 22) remove 메서드
- 최댓값이 삭제되기 때문에 루트 노드가 제거됨
- 트리 마지막 자리 노드를 임시로 루트 노드 자리에 배치
- 자식 노드들과 키 값을 계속 비교하면서 값이 더 크면 아래로 이동시킴
- 자식 노드가 두 개인 경우 더 큰 값을 가진 자식 노드 쪽으로 이동함
- 원소의 개수가 n인 최대 힙에서 최대 원소를 삭제
- 자식 노드들과의 대소 비교 최대 횟수 : 2 * log2n
- worst case에서의 복잡도 O(logn)
def remove(self):
if len(self.data) > 1:
# 트리 마지막 자리 노드를 임시로 루트 노드 자리에 배치
self.data[1], self.data[-1] = self.data[-1], self.data[1]
data = self.data.pop(-1) # 최댓값 삭제
self.maxHeapify(1) # 재귀 호출로 max heap 조건 만족
else:
data = None
return data
def maxHeapify(self, i):
left = i * 2 # left child 인덱스 계산
right = i * 2 + 1 # right child 인덱스 계산
smallest = i # 자기 자신으로 초기화
# 왼쪽 자식이 존재하는지, 그리고 왼쪽 자식의 키 값이 자신보다 더 큰지를 판단
if left < len(self.data) and self.data[left] > self.data[smallest]:
smallest = left # smallest는 왼쪽 자식의 인덱스를 갖게 됨
# 오른쪽 자식이 존재하는지, 그리고 오른쪽 자식의 키 값이 오른쪽 자식 또는 자기 자신보다 더 큰지를 판단
if right < len(self.data) and self.data[right] > self.data[smallest]:
smallest = right # smallest는 오른쪽 자식의 인덱스를 갖게 됨
if smallest != i: # 나보다 큰 값을 가진 자식 노드를 발견한 경우
# 현재 노드(인덱스 i)와 최댓값 노드(왼쪽 아니면 오른쪽 자식)를 교체
self.data[i], self.data[smallest] = self.data[smallest], self.data[i]
# 재귀적 호출을 이용하여 최대 힙의 성질을 만족할 때까지 트리를 정리함
self.maxHeapify(smallest)3. max/min heap 응용
1) 우선 순위 큐
- Enqueue를 할 때 느슨한 정렬을 이루고 있도록 함 : O(logn)
- Dequeue를 할 때 최댓값을 순서대로 추출 : O(logn)
2) heap sort
- 정렬되지 않은 원소들을 아무 순서로 최대 힙에 삽입 : O(logn)
- 삽입이 끝나면, 힙이 비게 될 때까지 하나씩 삭제함 : O(logn)
- 원소들이 삭제된 순서가 원소들의 정렬 순서가 됨
- heap sort 알고리즘의 복잡도 : O(nlogn)
def heapsort(unsorted):
H = MaxHeap()
for item in unsorted: # 정렬되지 않은 원소들을 전부 최대 힙에 삽입
H.insert(item)
sorted = []
d = H.remove()
while d: # 힙이 빌 때까지
sorted.append(d) # 원소들을 하나씩 삭제하고 삭제된 원소들을 새로운 리스트에 저장
d = H.remove()
return sorted