
1. Trees
-
정점과 간선을 이용하여 데이터의 배치 형태를 추상화한 자료 구조
-
노드의 level : root node를 level 0으로 생각
-
노드의 degree : child(subtree)의 수
degree = 0 : leaf node
-
트리의 height(depth) : root node만 있을 때의 높이는 1
-
이진 트리 (binary trees) : 모든 노드의 차수가 2 이하인 트리
재귀적으로 정의 가능 : empty tree이거나,
루트 노드 + 왼쪽 서브트리 + 오른쪽 서브트리
(단, 왼쪽과 오른쪽 서브트리 또한 이진 트리) -
포화 이진 트리 (full binary trees) : 모든 레벨에서 노드들이 모두 채워져 있는 이진 트리
height = k 이고 nodeCount = 2^k - 1 인 이진 트리
-
완전 이진 트리 (complete binary trees) :
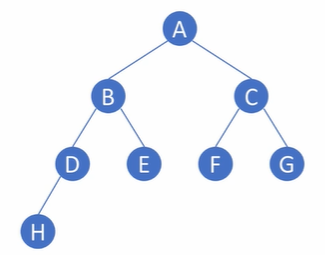
높이가 k인 완전 이진 트리의 경우
level k-2까지는 모든 노드가 2개의 자식을 가진 포화 이진 트리
level k-1에서는 왼쪽부터 노드가 순차적으로 채워져 있는 이진 트리
2. Binary Trees
1) 연산 정의
- size() : 현재 트리에 포함되어 있는 노드의 수를 구함
- depth() : 현재 트리의 깊이(또는 높이)를 구함
- traversal (순회)
Depth First Traversal : 깊이 우선 순회
Breadth First Traversal : 넓이 우선 순회
2) 이진 트리 구현
-
Node : Data, left child, right child
-
size와 depth는 재귀적으로 구할 수 있음
-
전체 이진 트리 size()
= left subtree size() + right subtree size() + 1(자기자신) -
전체 이진 트리의 depth()
= left subtree depth()와 right subtree depth() 중 더 큰 것 + 1
class Node:
def __init__(self, item):
self.data = item
self.left = None # left child
self.right = None # right child
# left subtree size() + right subtree size() + 1(자기자신)
def size(self):
l = self.left.size() if self.left else 0
r = self.right.size() if self.right else 0
return l + r + 1
# left subtree depth()와 right subtree depth() 중 더 큰 것 + 1
def depth(self):
l = self.left.depth() if self.left else 0
r = self.right.depth() if self.right else 0
if l > r:
d = l
else:
d = r
return d + 1
class BinaryTree:
def __init__(self, r):
self.root = r # root만 알고 있으면 됨
def size(self):
if self.root: # root node가 존재하는지 확인
return self.root.size()
else: # empty tree인 경우
return 0
def depth(self):
if self.root:
return self.root.depth()
else:
return 03. DFT (Depth First Traversal)
- Depth First Traversal : 깊이 우선 순회
- 재귀적으로 구현할 수 있음
in-order traverasl (중위 순회)
: left subtree -> 자기 자신 -> right subtree
pre-order traversal (전위 순회)
: 자기 자신 -> left subtree -> right subtree
post-order traversal (후위 순회)
: left subtree -> right subtree -> 자기 자신
class Node:
def __init__(self, item):
self.data = item
self.left = None # left child
self.right = None # right child
def inorder(self): # 전위 순회
traversal = []
if self.left: # (1) left subtree
traversal += self.left.inorder()
traversal.append(self.data) # (2) 자기 자신
if self.right: # (3) right subtree
traversal += self.right.inorder()
return traversal
def preorder(self): # 전위 순회
traversal = []
traversal.append(self.data) # (1) 자기 자신
if self.left:
traversal += self.left.preorder()
if self.right:
traversal += self.right.preorder()
return traversal
def postorder(self): # 후위 순회
traversal = []
if self.left:
traversal += self.left.postorder()
if self.right:
traversal += self.right.postorder()
traversal.append(self.data) # (3) 자기 자신
return traversal
class BinaryTree:
def __init__(self, r):
self.root = r
def inorder(self):
if self.root:
return self.root.inorder()
else:
return []
def preorder(self):
if self.root:
return self.root.preorder()
else:
return []
def postorder(self):
if self.root:
return self.root.postorder()
else:
return [] 4. BFT (Breadth First Traversal)
-
Breadth First Traversal : 넓이 우선 순회
-
level이 낮은 노드를 우선으로 방문
-
level이 같은 경우 부모 노드의 방문 순서에 따라 방문하고,
왼쪽 자식 노드를 오른쪽 자식보다 먼저 방문 -
재귀적으로 구현하기에 적합하지 않음
-
한 노드를 방문했을 때, 나중에 방문할 노드들을 순서대로 기록
=> Queue를 이용하여 구현
=> Q가 빈 큐가 되면 모든 노드 방문 완료
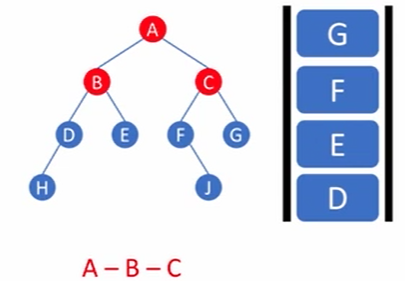
level 2 : D, E, F, G
Q.dequeue() => D를 뽑아내고 자식 노드인 H를 큐에 집어넣음
BFT : A - B - C - D - E - F - G - H - J
class ArrayQueue:
def __init__(self):
self.data = []
def size(self):
return len(self.data)
def isEmpty(self):
return self.size() == 0
def enqueue(self, item):
self.data.append(item)
def dequeue(self):
return self.data.pop(0)
def peek(self):
return self.data[0]
class Node:
def __init__(self, item):
self.data = item
self.left = None
self.right = None
class BinaryTree:
def __init__(self, r):
self.root = r
def bft(self): # 넓이 우선 순회
traversal = []
q = ArrayQueue()
if self.root: # 빈 트리가 아니면 root node를 q에 추가
q.enqueue(self.root)
while not q.isEmpty(): # q가 비어 있지 않는 동안
# q에서 추출한 node 방문
node = q.dequeue()
traversal.append(node.data)
# node의 left, right child가 있으면 q에 추가
if node.left:
q.enqueue(node.left)
if node.right:
q.enqueue(node.right)
return traversal