그래프(Graph)
기본구조
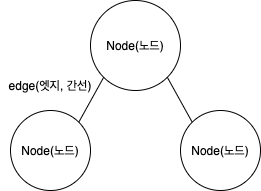
그래프는 node(노드)와 edge(엣지)로 표현되는 자료구조이다. node 와 edge를 각각 vertex, arc라고 부르기도 한다. 각 node는 값을 가질 수 있고, weighted graph라면 edge도 weight 값을 가질 수 있다. 또, edge가 방향성이 있어서 A => B 와 B => A 가 다른 경우, Directed graph라고 한다.
표현방식
그래프를 프로그래밍으로 표현할 수 있는 방법은 인접 행렬(Adjacency Matrix), 인접 리스트(Adjacency List) 두 가지가 있다.
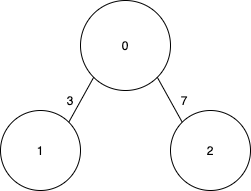
위의 그래프는 간단한 weighted graph 이다. 이 그래프를 두 방식으로 표현해 볼 수 있다.
인접 행렬(Adjacency Matrix)
인접 행렬 방식은 2차원 배열에 각 노드가 연결된 형태를 기록하는 방식이다. 파이썬의 경우, 리스트 자료형을 사용하여 나타낼 수 있다.
INF = 999999999
# 2차원 리스트로 인접 행렬 표현
graph = [
[0,3,7],
[3,0,INF],
[7,INF,0]
]graph[0]이 0번 node와 다른 node들 간 연결상태를 나타내는 리스트 [0,3,7]을 가진다. 자기 자신과의 연결상태는 0으로 나타내고, edge로 연결되지 않을 경우, INF로 무한대로 나타낸다.
인접 리스트(Adjacency List)
인접 리스트 방식은 Linked List(연결 리스트)라는 자료구조를 사용해서 그래프의 연결상태를 나타낸다. 파이썬의 경우, 기본 자료형인 리스트 자료형을 사용해서 linked list의 기능을 표현할 수 있으므로 이 경우에도 2차원 리스트를 사용해서 표현한다.
# 노드가 3개인 그래프 => 행이 3개인 2차원 리스트로 표현
graph = [[] for _ in range(3)]
# node 0
graph[0].append((1,3)) #연결정보를 (노드번호, weight)의 tuple로 표현
graph[0].append((2,7))
# node 1
graph[1].append((0,3))
# node 2
graph[2].append((0,7))위처럼 2차원 리스트로 linked list를 표현하고, 각 node 번호에 해당하는 list에 (연결된 노드 번호, weight(거리))형태의 tuple로 연결 정보를 저장한다.
두 표현방식 장단점
두 표현방식은 시간복잡도, 공간복잡도의 측면에서 차이가 있다.
노드의 개수를 N, 엣지의 개수를 E라고 할 때,
인접 행렬의 경우,
특정 두 node 간의 edge 존재여부를O(1)의 시간안에 찾을 수 있다. 2차원 matrix에 바로 접근하면 되기 때문이다. node의 차수는O(N)안에 알 수 있다. 전체 edge를 탐색할 경우O(N^2)의 시간이 소요된다.
하지만 메모리의 측면에서O(N^2)만큼의 메모리가 필요해서 node간에 edge가 존재하지 않는 메모리 공간이 낭비된다.인접 리스트의 경우,
특정 두 node 간의 연결 정보를 알기 위해서 소요되는 시간은 해당 node에 연결된 edge의 개수에 따라 달라진다. 전체 edge를 탐색하는 경우O(N+E)의 시간이 소요된다.
메모리의 경우, 각 node와 각 node에 연결된 edge를 표현해야 하므로O(N+E)의 공간복잡도가 소요된다.
따라서 인접 행렬의 경우, 그래프에 edge가 많이 존재하는 Dense graph에서 유리하고, 인접 리스트의 경우 edge가 많이 없는 Sparse graph에서 유리한 표현방식이다.
