[DirectX11 Pipeline] 4. Rasterizer

SYiee·2023년 8월 18일

Computer Graphics DirectX Graphics Pipeline

Graphics Pipeline (DirectX11)

목록 보기

4/6

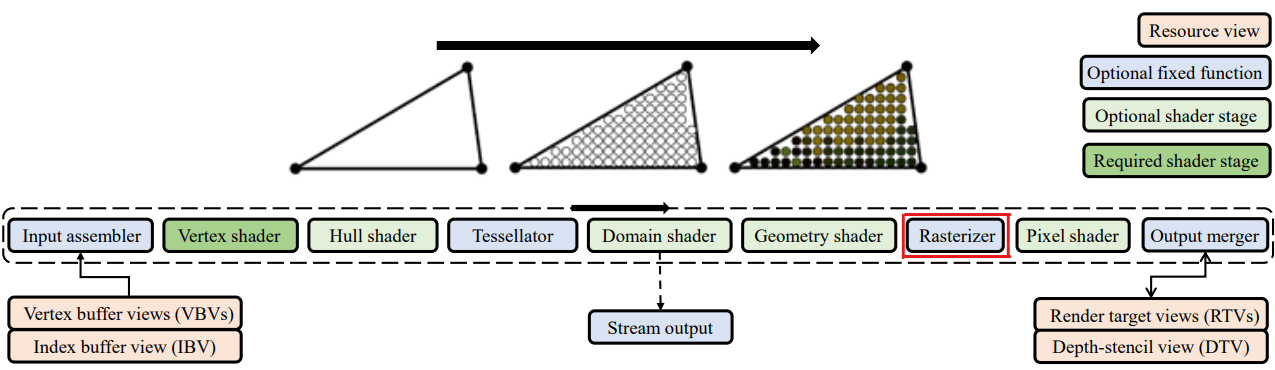
🖤 Rasterizer Stage

primitive 안을 pixel로 나누고 각 pixel의 색상, texture coordinate 등을 결정하는 단계

💡 Introduction
Rasterizer Stage는 개별적인 primitive(예: 삼각형)를 샘플 영역 내의 커버리지에 기반하여 pixel 또는 fragment라고 불리는 2차원 이미지 요소로 분해하는 과정이다.

Rasterizer Stage에서는 primitive의 속성인 색상과 텍스처 좌표 등이 primitive를 구성하는 pixel에 대해 보간되어 전달된다. 이를 통해 화면에 primitive의 외형을 정확하게 표현할 수 있다.

Rasterizer 후, 결과적으로 생성된 pixel은 픽셀 셰이딩 및 블렌딩과 같은 그래픽 파이프라인의 추가 단계를 거쳐 최종적인 색상 및 기타 속성이 결정되며, 이후 화면에 표시된다.

앞서 VS에서 clip spapce position을 받아서 넘어왔다. Rasterizer에서는

Primitive Clipping

Perspective Division

Viewport Transform

와 같은 일을 한다. Rasterizer는 미리 만들어둔 형태로 작동을 한다.

Hull shader, Tessellator, Domain shader ⇒DX11에서 등장
Geometry shader ⇒ DX10에서 등장

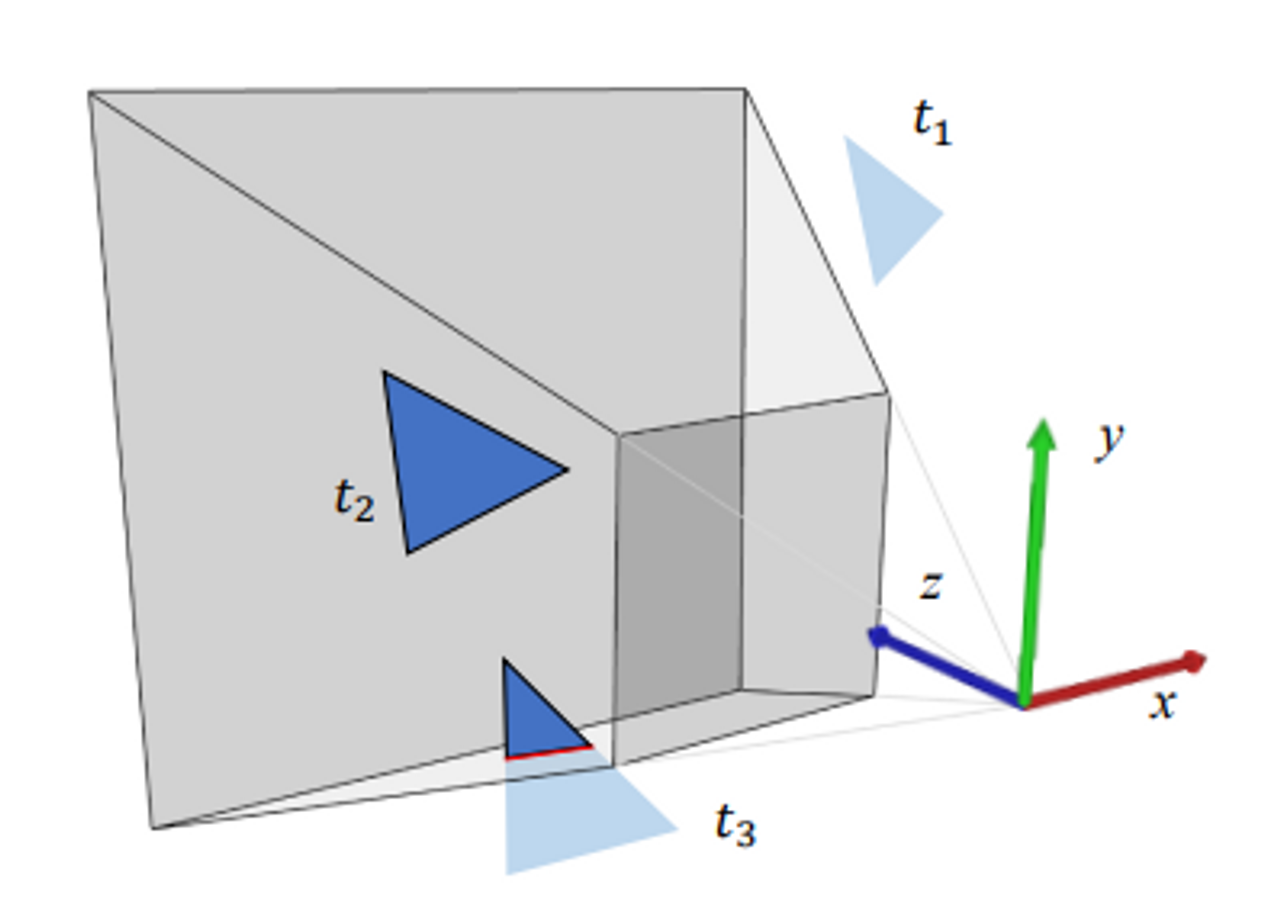
📌 Primitive Clipping

Triangle t2는 view frustrum안에 완전히 들어와 있다. t3는 clip 되었다.

clipping volume 밖에 있는 것들은 clip이 된다. 여기에는 몇가지 룰이 있다.
- Points :
  - clipping volume 밖에 있으면 자른다
  - 포인트가 1 픽셀보다 클 때 중점 좌표로 비교해서 안에 있으며 살리고 아니면 자른다.
- Lines : 선이 잘리면 그 잘린 지점에 vertex를 하나 만들고 잘린 부분은 버리고 나머진 살리고
- Triangles : 잘린 부분의 vertex를 생성해 살리고
  
  삼각형이 시야 볼륨에 클리핑되면, 클리핑 볼륨 경계에 있는 정점을 가진 적절한 삼각형이 생성된다.

📌 Perspective Division

clip space coordinate의 z값으로 모든 좌표계를 나누어 z 값이 1인 NDC(normalized device coordinates) 로 표현하는 것

z로 나누어 주는 것
z : the distance from the xy-plane of the camera space
z로 나누어 주는 과정은 멀리 있는 것은 작아지고 가까이 있는 것은 커짐으로 원근이 생긴다.
The result is said to be in NDC (normalized device coordinates).
→ z로 나누어 주고 난 후

projection matrix를 곱해서 clip space로 날아갔다. 그 후 z의 좌표계만큼 나누어주면 NDC로 간다.

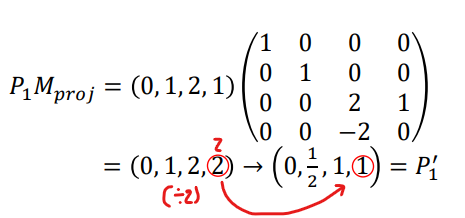
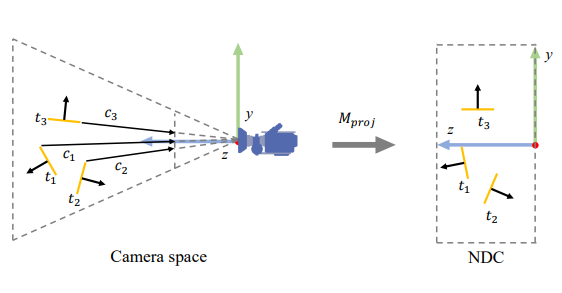
📌 Viewport Transform

NDC에서 만든 것을 screen space로 옮기기 위한 작업 이 필요하다

Viewport Transform

The ‘viewport transform’ transforms vertex positions from NDC space(Clip space) to window space(viewport)

앞서 Perspective Division을 통해 구한 Clip space(NDC) → Viewport(window space)로의 변환과정이다.

이 변환은 affine transform에 해당

아래 그림과 같이 scaling과 translation을 합친 형태의 Viewport Transform matrix를 통해 연산이 이루어 진다.

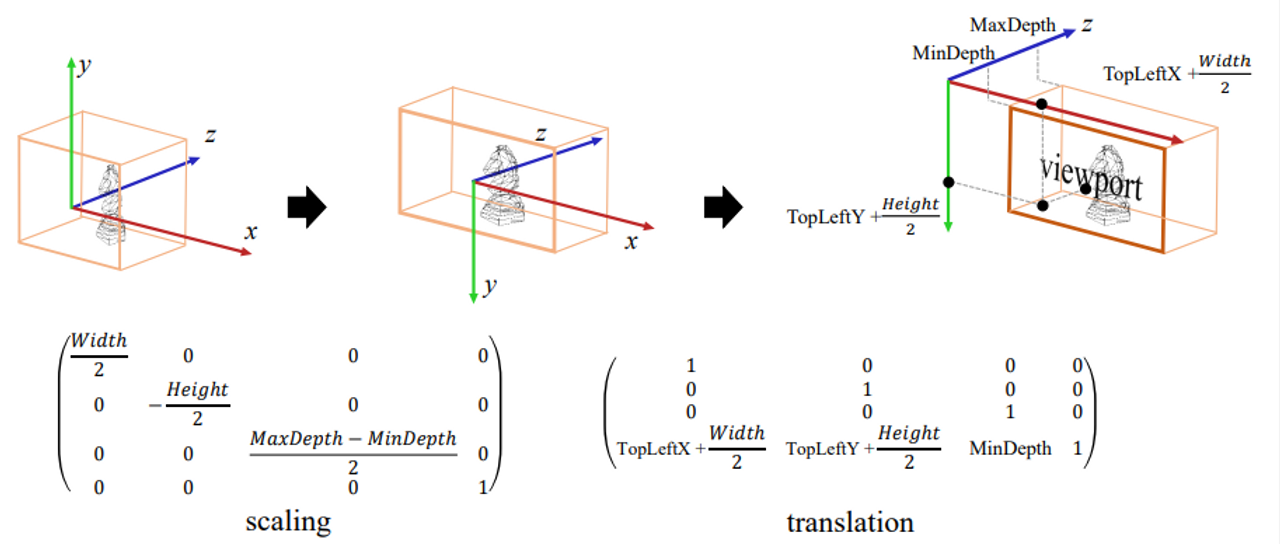
Viewport
Viewport는 쉽게 말해서 이제 모니터 속 공간(이지만 아직 3D)을 나타내는 공간이다. clip space는 보이는 물체를 솎아내고 Perspective Division를 통해 그에 맞는 원근을 표현했지만 이는 camera가 보는 시점에서의 기준이다. 이제 우리는 모니터의 비율에 맞게 공간에 clip space의 정보들을 맵핑하고자 한다. Viewport를 정의하는 변수로는 w, h, minX, minY, minZ, maxZ가 있다.

모니터를 full로 쓴다고 했을 때 식이 다음과 같이 간단해진다.

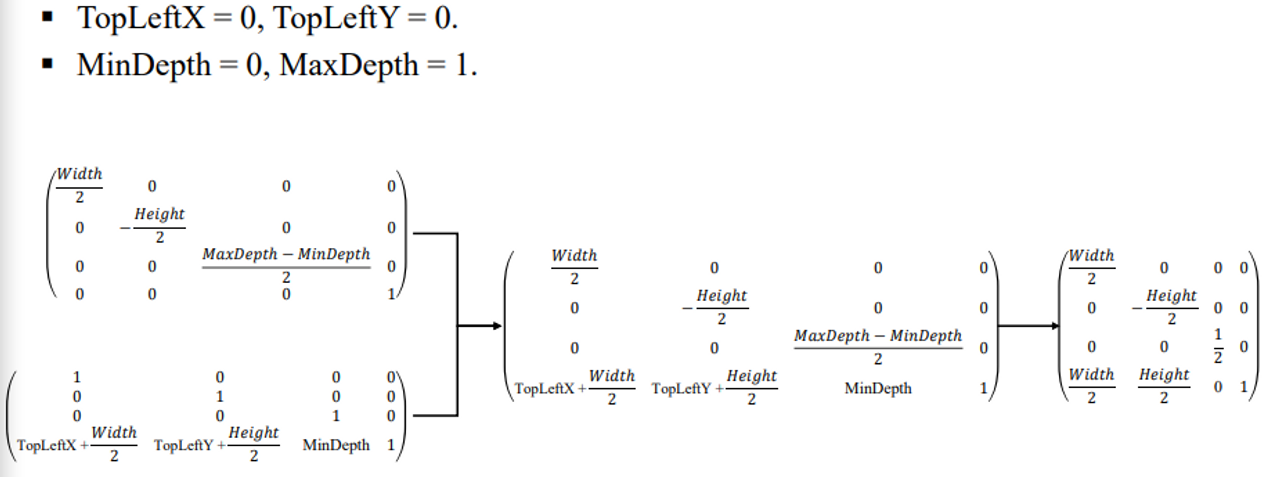
📌 Face Culling

camera에서 보기에 3D object의 뒷면에 해당하는 부분 어차피 보이지 않는다. clip space를 만드는 view transform을 통해 View Frustum 밖의 object를 Culling 했듯, cost를 줄이기 위해 보이지 않는 object의 뒷면도 Culling 하고자 한다.

그렇다면 어떻게 컴퓨터가 object의 뒷면과 앞면을 구분할까? 답은 normal vector를 정의한 부분에서 알 수 있다. 이 Normal Vector의 방향이 object의 바깥쪽을 향하는 것이 원칙임을 이용한다.

💡 Back-face Culling
Primitives have a particular facing that is defined by the order of vertices.

cost를 줄이기 위해 object에 뒷면에 있는 것은 지운다,

nomal vecter의 회전 방향을 이용해 뒷면에 있는 것인지 판단한다.

이때 det식을 활용한다.

primitives가 어떤 순서로 되어 있냐에 따라 face가 어디를 바라보고 있는지 결정이 된다.
n1은 거의 선으로 보이게 되나. 완전히 반대가 되면 back face로 렌더링을 안해준다. 요즘은 back face를 하는 추세이다. 복잡한 mesh들이 생겨나면서 back face를 그려주는게 편하다. 성능 아낄꺼면 렌더링 안하면 된다.
face culling은 back face에 해당하는 부분은 이후에 프로세싱을 진행하지 않겠다고 잘라주는 것이다.

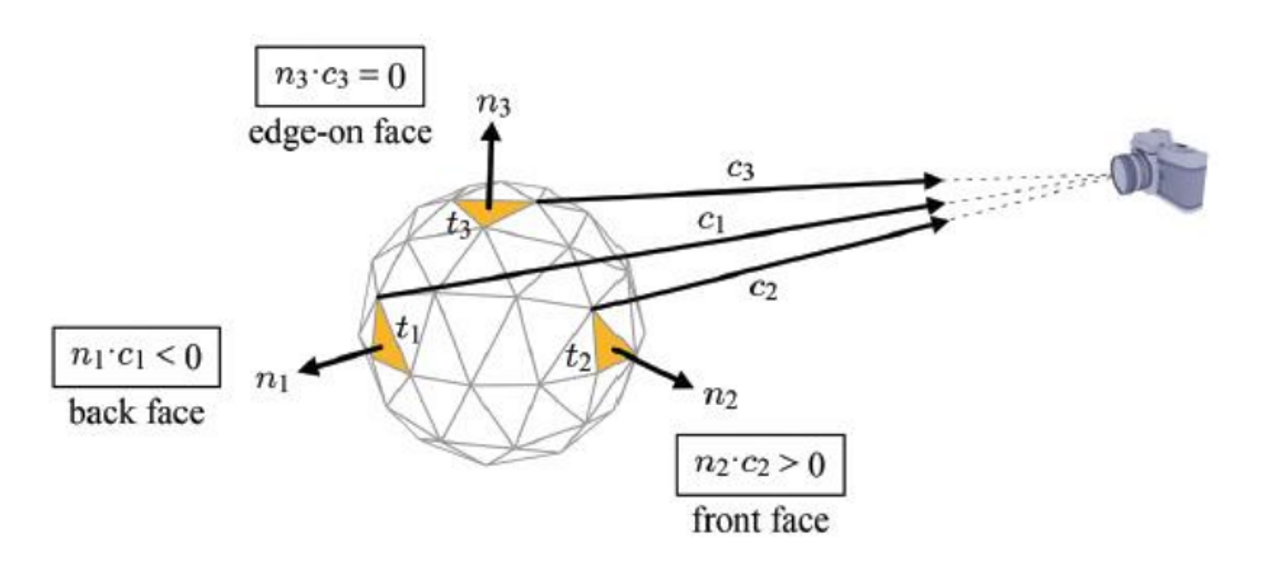
det로 정점이 뒷면에 있는지 앞면에 있는지 판단할 수 있다.

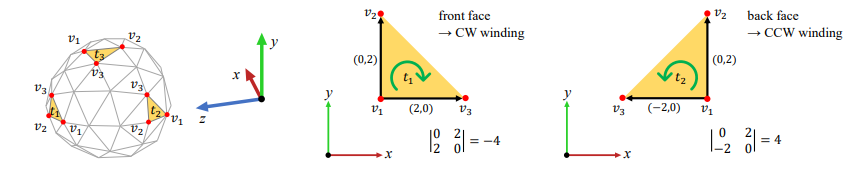
If negative, CW and so front-face.
If it is positive, CCW and so back-face.
If 0, edge-on face.(옆면)

xy plane으로 옮겨 왔을 때 font에 있는 vertex는 CW로 돌고 뒷면에 있는 버텍스는 CCW로 회전한다. 이렇게 CW로 회전하는 것은 물체를 정면에서 바라보았을 때다. 180도 뒤집어진 오브젝트의 뒷면에 해당하는 nomal vecter를 가지고 있으면 이는 뒷면이라는 것을 알 수 있다. (OpenGL은 이와 반대이니 유의)

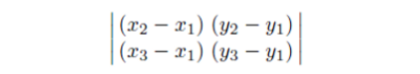
별도의 과정 없이 빠르게 계산할 수 있다.
back face는 항상 culling되는 것은 아니며 옵션으로 설정할 수 있다.

🖤 Rasterization

The main role of rasterization stage is to convert vector information into a raster image.

primitive의 래스터화는 두 가지 부분으로 이루어져 있다

윈도우 좌표의 정수 그리드에서 primitive가 차지하는 사각형을 결정하는 것

각각의 그리드 사각형에 색상과 깊이값을 할당하는 작업

위에서는 필요없는 것들을 버리는 작업을 했다. 이제 픽셀을 다루자!

어떤 위치에 있는지 어떤 깊이를 가지고 있는지
화면의 픽셀을 표시할 때 누가 앞에 있는지 알 수 없으니 자신의 depth를 알려주는 것
자기자신의 버텍스가 차지하는 픽셀값 뿐만 아니라 픽셀의 깊이 정보도 포함이된다. -> rgbd

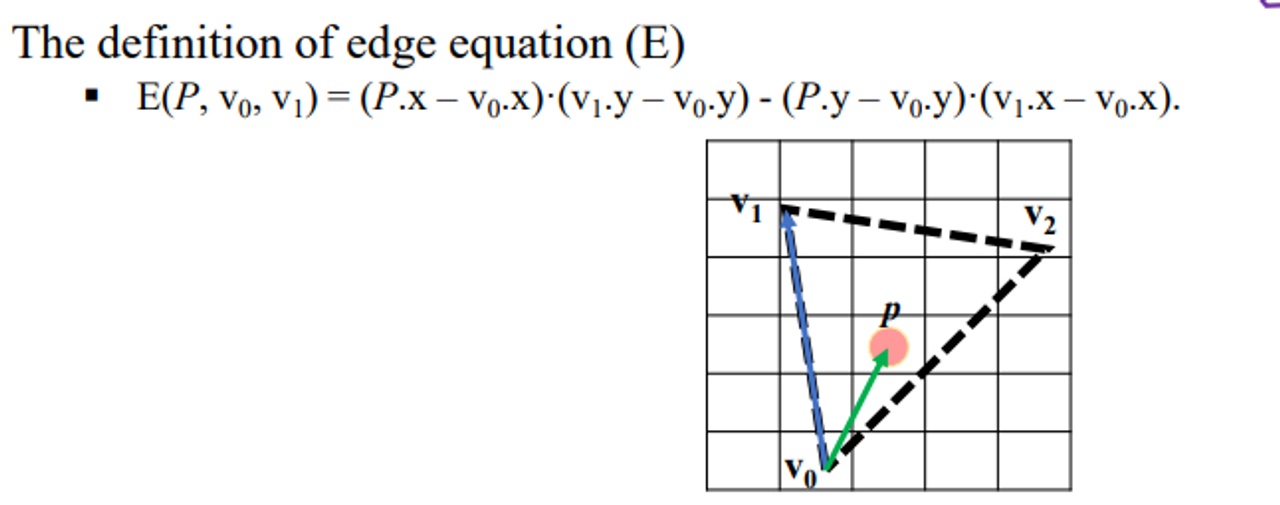
📌 Edge Equation

Edge equation을 이용해 삼각형 안에 있는 점인지 판단

2d 플레인을 두개로 나누어준다

주어진 라인을 기준으로 왼쪽인지 오른쪽인지 리턴해주는것이 edge equation 함수이다.

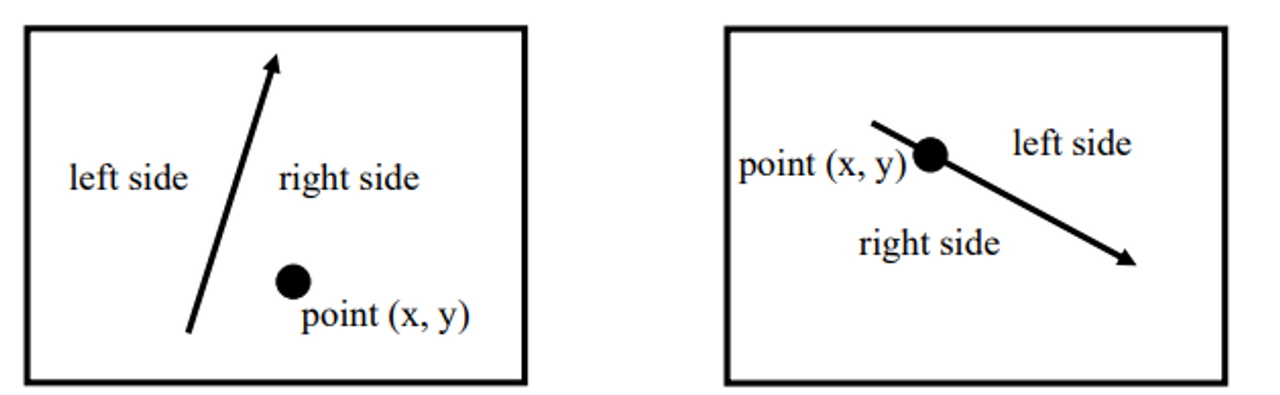
Edge equation tests on which side of this line a given point is.

When the point is on the left side: negative number.
When the point is on the right side: positive number.
When the point is on the line: zero number.

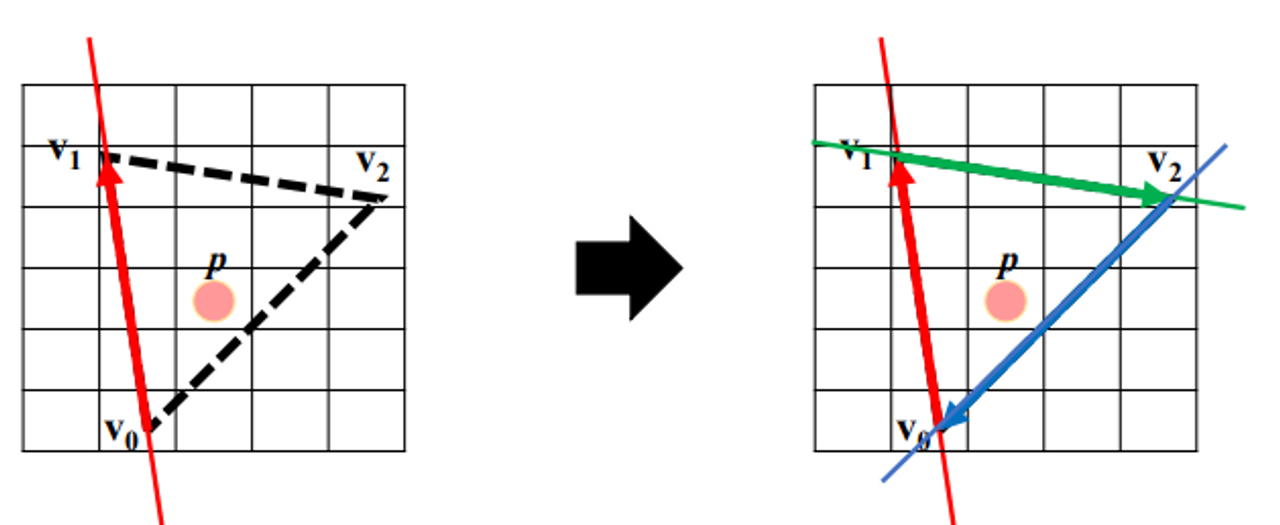
점 p는 3개의 엣지를 기준으로 모두 오른쪽에 있으니 삼각형 내부에 있다는 것을 알 수 있다.
→ the edge function returns positive numbers with respect to all three edges of triangle

Edge Equation 정의

2D
det가 양수냐 음수냐로 판단이 가능하다

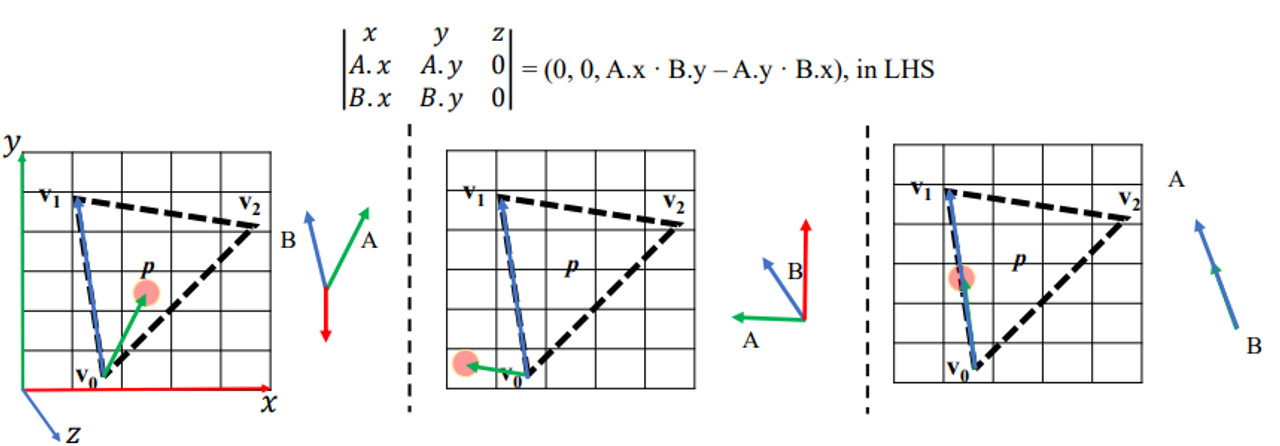
3D

the magnitude of the cross products

cross product magnitude 구하는 것과 같다

0 < θ < 180 : magnitude = posivive
180 < θ < 360 : magnitude = negative

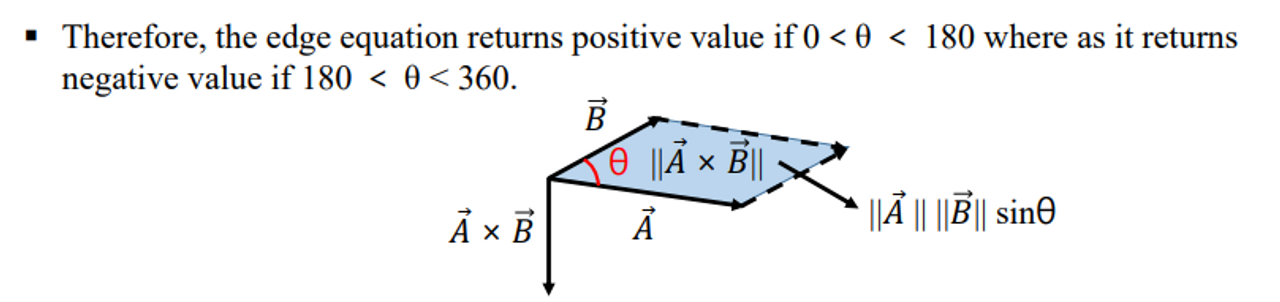
cross products 의 magnitude는 마름모의넓이와 같다. - absin

→ sin이니 0-180은 양수를 180을 넘어가면 음수결과를 갖는다

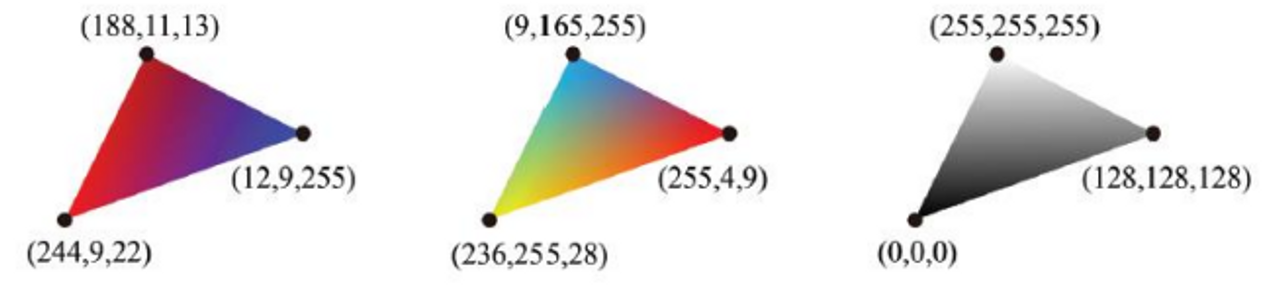
📌 Assigning Attributes for Fragments

삼각형(v0v1v2)과 겹치는 점(p)의 속성(색상, 깊이, 법선 등)은 삼각형의 정점의 속성을 보간하여 얻을 수 있다.

v0, v1, v2의 색상을 Cv0, Cv1, Cv2라고 가정
그런 경우, p의 색상을 Barycentric coordinate를 사용하여 다음과 같이 계산할 수 있다: (p∈△v0,v1,v2일 때)
- p = λ0∗Cv0 + λ1∗Cv1 + λ2∗Cv2,
- λ0 + λ1 + λ2 = 1,
위치, 깊이, 법선도 이 방법을 사용하여 계산할 수 있다.

Barycentric coordinate 를 이용해 interpolate한다.

Barycentric coordinate

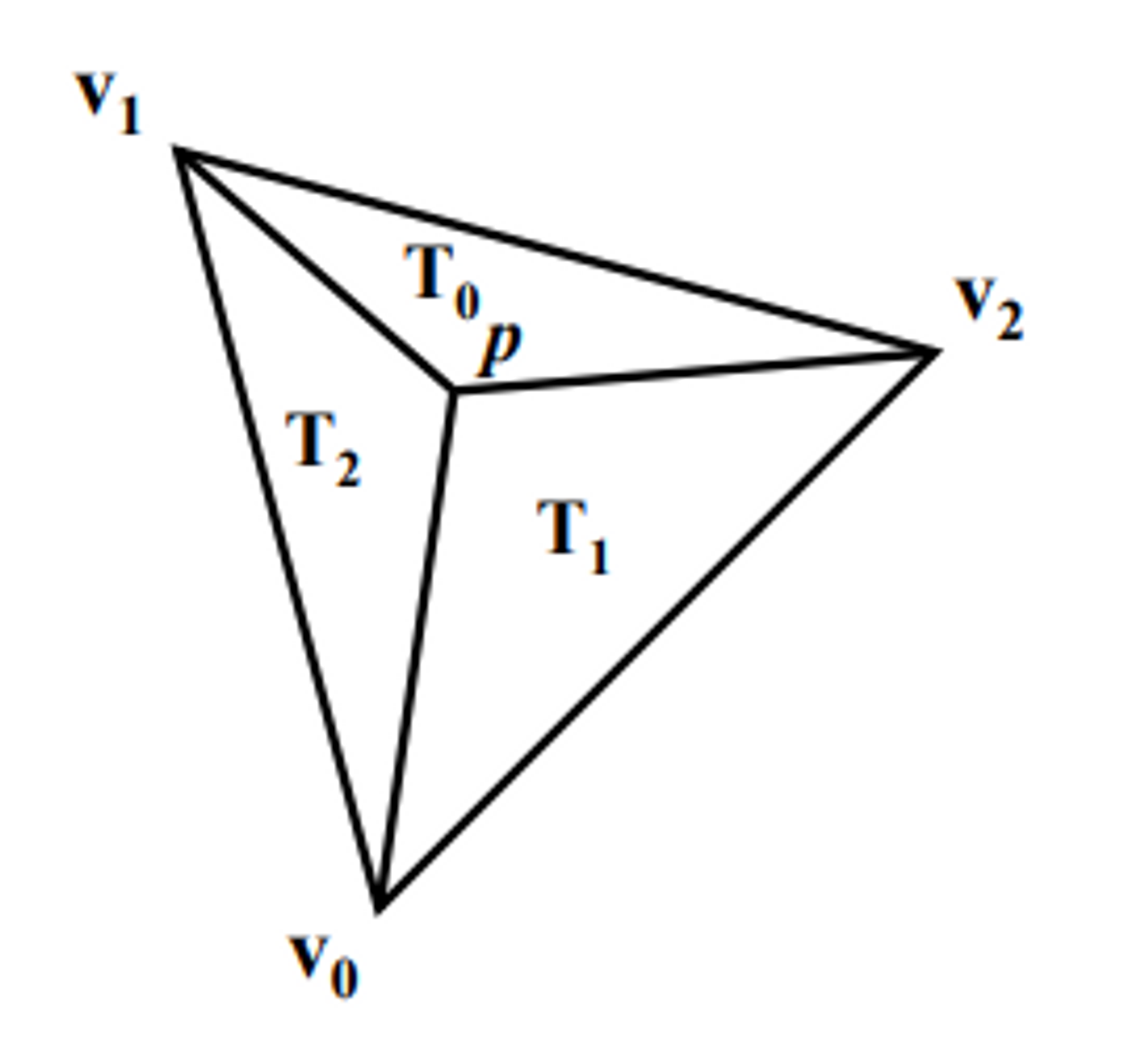
Barycentric coordinate 의 가중치(λ0, λ1, λ2)는 삼각형(T0, T1, T2)의 면적과 비례한다.

T0은 0.5 * E(p, v1, v2)로 계산할 수 있습니다. 여기서 edge equation은 평행사변형의 면적을 반환
T1은 0.5 * E(p, v2, v0)로 계산할 수 있습니다. 여기서 edge equation은 평행사변형의 면적을 반환
T2는 0.5 * E(p, v0, v1)로 계산할 수 있습니다. 여기서 edge equation은 평행사변형의 면적을 반환
삼각형 v0v1v2의 면적은 0.5 * E(v2, v0, v1)로 계산할 수 있다.
따라서, λ0 = E(p, v1, v2) / E(v2, v0, v1), λ1 = E(p, v2, v0) / E(v2, v0, v1), 그리고 λ2 = E(p, v0, v1) / E(v2, v0, v1) 이다.
-> 전체 넓이에 대한 해당 삼각형의 넓이 비율

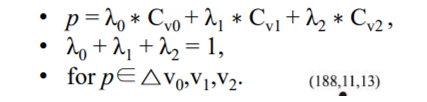
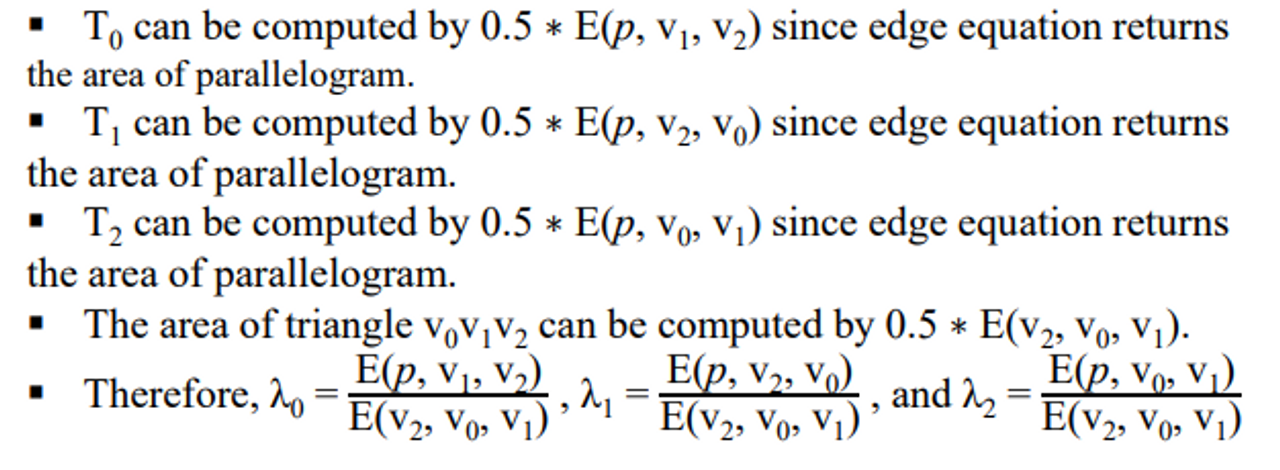
edge equation returns the area of parallelogram.
→ 넓이를 바로 구할 수가 있다. 성능이 좋다.

Rasterization Rule (Top-left Rule)

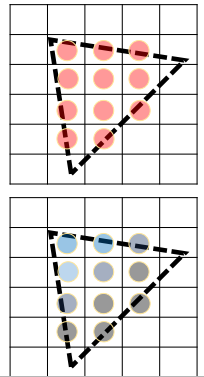
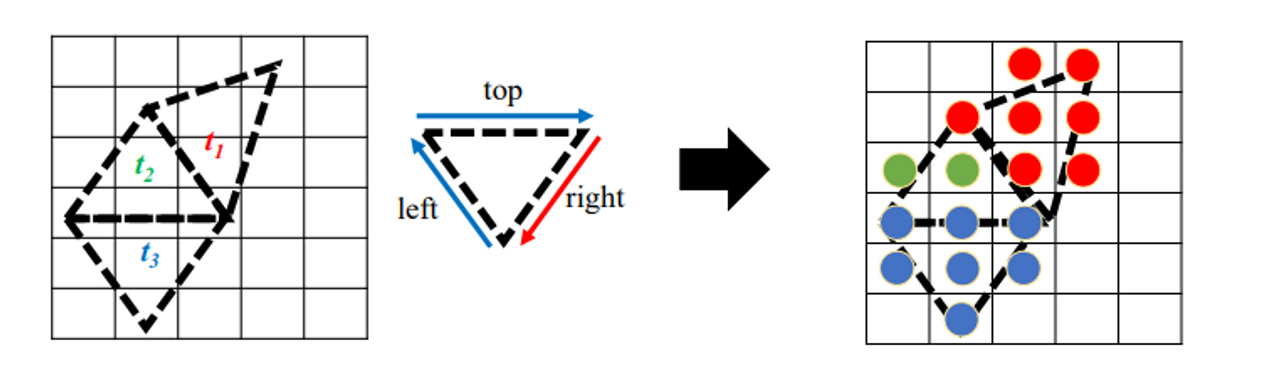
점이 두 삼각형 위에 있을 때 top부분에 먼저 assign 그다음 right left 순으로 assign

한 픽셀이 두 개의 삼각형에 공유되는 가장자리에 위치할 경우, 어느 삼각형에 속하는지 결정해야 한다. 그렇지 않으면 해당 픽셀이 두 번 처리될 수 있기 때문이다.

직관적으로, 삼각형은 왼쪽, 오른쪽, 위쪽 또는 아래쪽 가장자리를 갖을 수 있다.
아래 그림에서, t1은 두 개의 왼쪽 가장자리와 하나의 오른쪽 가장자리를 갖고 있으며, t2는 하나의 왼쪽 가장자리, 하나의 오른쪽 가장자리 및 하나의 아래쪽 가장자리를 갖고 있으며, t3는 하나의 왼쪽 가장자리, 하나의 오른쪽 가장자리 및 하나의 위쪽 가장자리를 갖고 있다.
Direct3D는 Top-left Rule을 채택하며, 이는 픽셀이 삼각형의 상단 가장자리 또는 왼쪽 가장자리에 위치한 경우 해당 삼각형에 속한다고 선언한다.