알고리즘 문제를 풀면서 실수 연산을 하다보면, 예상한 것과 결과가 다르게 나오는 경우가 종종 있다.

이러한 원인은 컴퓨터가 실수를 표현하는 방식에 있다. 컴퓨터가 실수를 표현하는 방식을 알아보고, 오차 발생 이유를 알아보자.

실수 표현 방식

컴퓨터는 모든 수를 0과 1로 이루어진 2진수로 표현한다. 이것은 정수뿐만 아니라 소수점이 존재하는 실수도 마찬가지이다.

정수의 경우 이러한 표현이 간단하지만, 실수를 2진수로 표현하는 것은 복잡하다. 실수를 표현하기 위한 다양한 방법들이 연구되었으며 현재는 크게 2가지 방식이 존재한다.

1. 고정 소수점 (fixed point) 방식
2. 부동 소수좀 (floating point) 방식

고정 소수점 (fixed point) 방식

실수는 보통 정수부와 소수부로 나눌 수 있다. 따라서 실수를 표현하는 가장 간단한 방법은 소수부의 자릿수를 미리 정하고, 고정된 자릿수의 소수를 표현하는 것이다.

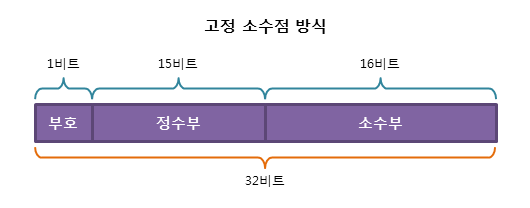
32비트 CPU에서 고정 소수점 방식으로 실수를 표현하면 위와 같다.

하지만, 이 방식은 정수부와 소수부의 자릿수가 크지 않으므로, 표현할 수 있는 범위가 매우 적다는 단점이 있다. 또한 따라오는 단점으로는 정밀도가 낮다는 특징이 있다. 따라서 높은 정밀도가 필요없는 소규모 시스템에서만 간혹 쓰인다.

부동 소수점 (floating point) 방식

실수는 보통 정수부와 소수부로 나누지만, 가수부와 지수부로 나누어 표현할 수도 있다.

부동 소수점 방식은 실수를 a*2^b 형식으로 저장한다.

이때 a는 1보다 크거나 같고, 2보다 작은 실수이다.

±(1.가수부)×2^지수부-127

앞서 살펴본 고정 소수점 방식은 제한된 자릿수로 인해 표현할 수 있는 범위가 매우 작다. 하지만, 부동 소수점 방식은 위의 수식을 이용하여 매우 큰 실수까지도 표현할 수 있다.

현재 대부분의 시스템에서는 부동 소수점 방식으로 실수를 표현할 수 있다.

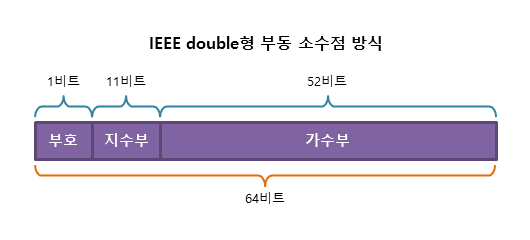
64비트 CPU의 double형 실수를 IEEE 부동 소수점 방식으로 표현하면 위와 같다.

지수부는 자릿수(크기)를 나타내는 부분이다. 즉 가수의 어디쯤에 소수점이 있는지 나타낸다.

가수부는 실수의 실제 값을 표현하는 부분이다.

부동 소수점 방식 오차

부동 소수점 방식은 고정 소수점 방식보다 훨씬 더 많은 범위까지 표현할 수 있지만, 항상 오차가 존재한다는 단점을 가지고 있다.

부동 소수점 방식에서 오차는 위에서 살펴본 공식에 의해 발생한다.

해당 공식을 사용하면 표현할 수 있는 범위는 늘지만, 10진수를 정확하게 표현할 수는 없다. (무한소수, 순환소수의 경우 가수부가 표현할 수 있는 비트 수를 넘어가게 되면 손실되는 부분이 생기기 때문, 실수 또한 이진수로 표현하기 때문에 가수부가 1/2^n 꼴로 표현되는 경우만 오차없이 정확하게 값이 계산된다.)

부동 소수점 방식 실수 표현할 때 발생하는 오차

double num = 0.1;

for(int i = 0; i < 1000; i++) {

    num += 0.1;

}

System.out.print(num);

실행결과

100.09999999999859

위의 예제에서 0.1을 1000번 더한 합계는 100이 되어야하지만, 실제로는 100.09999999999859가 출력된다.

이처럼 컴퓨터에서 실수를 가지고 수행하는 모든 연산에는 언제나 작은 오차가 존재하게 된다. 이것은 자바뿐만 아니라, 모든 프로그래밍 언어에서 발생하는 기본적인 문제이다.

자바 float, double 정밀도

float num3 = 1.23456789f;
double num4 = 1.23456789;

System.out.println("float형  변수 num3 : " + num3);
System.out.println("double형 변수 num4 : " + num4);

float형  변수 num3 : 1.2345679
double형 변수 num4 : 1.23456789

위의 예제는 float형 타입이 소수 6자리까지는 정확하게 표현할 수 있으나, 그 이상은 정확하게 표현하지 못함을 보여준다.

자바의 double형 타입은 소수부분 15자리까지 오차없이 표현할 수 있다. 하지만 그 이상의 소수 부분을 표현할 때는 언제나 작은 오차가 발생하게 된다.

---

참고 :
실수 표현방식
부동소수점 2진수 변환 - 꼭보기
부동소수점 오차 원인
부동소수점 오차 원인2