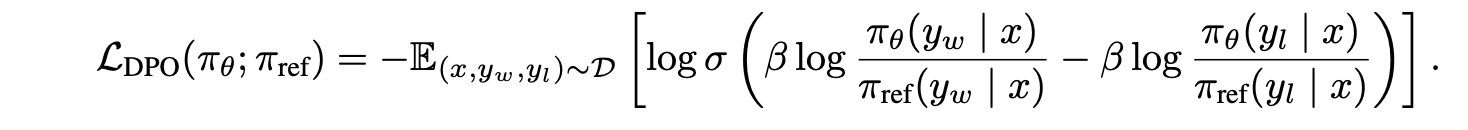Abstract

• LM은 다양한 지식과 추론 방법에 대해서 학습하지만 비지도 학습 방식(unsupervised nature of their training)때문에, LM을 제어하기 쉽지 않음.
• 그래서 지금 존재하는 방식은 human annotation 방식을 활용하여 human preferences를 align하는 방식으로 진행됨. 그리고 이러한 방법론적으로는 RLHF가 매우 유명함.
• 그러나 RLHF는 복잡하고, 불안정함.
• RLHF는 2단계로 진행된다.
  
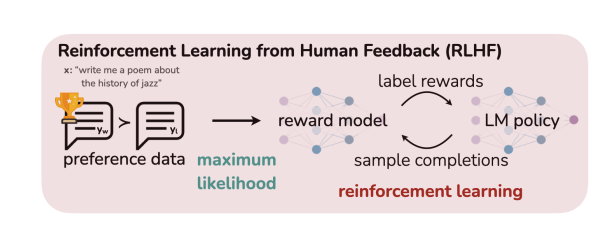
  1. 처음에 human preference를 나타내도록 reward model을 먼저 학습함.
  2. RL(reinforcement learning)을 활용하여 original model과 너무 차이나지 않도록 unsupervised LM을 통해 추정된 reward가 최대가 되도록 fine tuning함.
  
• 그러나 본 논문에서는 reward function과 optimal policy 사이의 매핑(?)을 활용하여 reward 최대화 문제를 2단계를 거치지 않고, 한 단계로 학습할 수 있는 방법을 제시함. -> DPO(Direct Preference Optimization)
• 위에서 RLHF의 단점인 불안정함과, 복잡한 단계를 단순화 시켜서, 안정적이고, 단순한 과정을 제시함.

Introduction

• Large Unsupervised language model은 대규모의 데이터셋을 통해 학습하여, 놀라운 성능을 보이고 있음.
• 그러나 이렇게 대규모 데이터셋을 학습할 때는, 다양한 사람들이 모은 데이터를 활용하기 때문에, 편향이 있거나, 잘못되었거나 등등의 데이터셋이 포함될 수도 있음.
• 그럼에도 불구하고, 우리는 모델이 그러한 오류를 잘 고쳐서 고품질의 답변을 생성하기를 원함.
• 그러하기 때문에, 이러한 alignment 문제들이 나오고 있는 것임.
• 기존 방식은 RL base인 방식이지만, 본 논문에서는 학습 파이프라인을 단순화하여, reward model 없이 RL-based objective가 간단한 binary cross entropy objective로 최적화될 수 있다는 것을 시사함.(아래 그림 참조)
  

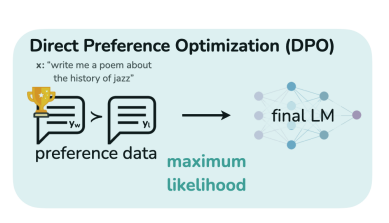
그럼 지금부터는 어떻게 reward model이 없이, 어떤 근거로 direct하게 human preference를 LM을 optimization 시키는지 알아보자.

• DPO를 직관적으로 생각했을 때는 사실 preferred response의 로그 확률을 dispreferred response의 로그 확률에 비해 증가시키고, 이것뿐만 아니라 dynamic, per-example importance weight도 활용한다고 하는데(모델의 degeneration 방지를 위해) 이 부분에 대해서는 이후에 의미를 알아보자.

---

-> 이러한 위의 글들을 읽으면 다음과 질문이 생긴다.
-> 왜 binary cross entropy objective라고 하는가? 도대체 식이 어떻고, loss가 어떻고, 최적화를 어떻게 하길래?
-> 모델의 degeneration을 구체적으로 어떻게 예방하는가? 단순히 preference만 강하게 학습시키지 않고, 기존의 성능도 어떻게 유지를 하는가?

---

• 사실 preference data를 language model에 주입시키는 가장 간단하고 직접적인 방법은 굉장히 퀄리티 높은 데이터를 활용해 SFT 방식으로 학습하는 것이다.
• 그러나 이렇게 하기에는 모든 경우의 퀄리티 높은 데이터를 준비할 수도 없고, 준비할 수 없다 보니 결국 모델은 봤던 데이터에 의존할 수도 있게 됨.
• RL은 이러한 문제점을 해결해줌. 더군다나 적절한 식을 통해 원본 모델과 너무 큰 차이가 나지 않게 함.

Preliminaries

그럼 일단 RLHF가 어떻게 되는지부터 다시 알아보자.
2단계라고 말하긴 했지만, SFT단계를 포함한다면 3단계이다.

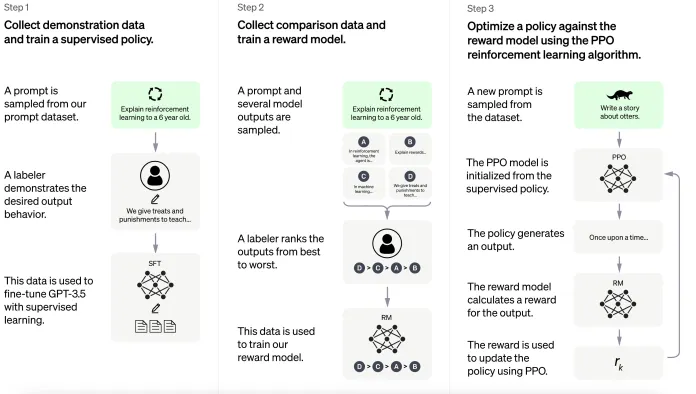
1. SFT
2. Reward Modeling Phase
3. RL Fine-Tuning Phase

1. SFT

• high quality 데이터로 학습시켜 $\pi^{SFT}$ 모델을 만들어낸다.

2. Reward Modeling Phase

• 학습된 $\pi^{SFT}$ 모델에게 $x(prompt)$를 주고 이에 따른 pair 답변 $y1(completion1), y2(completion2)$를 생성하게 한다.
• $y1$과 $y2$ 중 어느 답변이 더 선호되는지 사람에게 판단하게 한다.
• 그렇다면 이러한 선호도는 어떻게 쓰일까?
• 후에reward model을 통해 어떤 context $x$가 입력으로 들어왔을 때, $y$라는 response가 얼마나 좋은 것인지에 대한 보상을 주게 된다.
• 리워드 모델의 loss 함수는 다음과 같다.
  • $L_R(r_\phi,D) = -E_{(x, y_w, y_l)\sim D}[log\sigma(r_\phi(x, y_w) - r_\phi(x,y_l))]$
  • 위의 식을 해석해 보자면, context $x$가 주어졌을 때, $y_w$가 response로 주어질 때의 reward값(scalar값)과 context $x$가 주어졌을 때, $y_l$가 response로 주어질 때의 reward값(scalar값)의 차이이다.
  • 이를 sigmoid 함수를 활용하여 0과 1사이의 확률값으로 변환하여 모든 샘플들에 대한 기댓값을 더해준 뒤, 최종적으로 이 값이 작아지도록 하는 파라미터를 찾고자 하는 학습을 한다는 얘기이다.
  • 이를 좀 더 쉽게 풀어서 말하자면, log 함수를 통과하여 값이 작기 위해서는 시그모이드를 통과한 값이 커야 한다. 시그모이드 함수를 통과한 값이 크기 위해서는 리워드 값의 차가 커야 한다. 따라서, $y_w$ 경우의 reward값과 $y_l$ 경우의 reward값의 차가 커지는 방향으로 리워드 모델을 학습한다는 것이다.

3. RL Fine-Tuning Phase

• 학습된 리워드 모델을 활용하여 이제 SFT한 모델에 리워드를 주어야 한다.
• 리워드가 최대가 되는 방향으로 모델을 optimization하게 되는데, 식은 다음과 같다.
  • $\max_{\pi_\theta}E_{x\sim D, y\sim \pi_\theta(y|x)}[r_\phi(x,y)] - \beta D_{KL}[\pi_\theta(y|x)||\pi_{ref}(y|x)]$
  • 위의 식에 대한 해석을 하자면 리워드가 최대로 되는 최종모델의 파라미터($\pi_\theta$)를 찾는데, $\beta D_{KL}[\pi_\theta(y|x)||\pi_{ref}(y|x)]$ 이러한 수식의 부분을 통해 기존 모델(SFT만 된 모델)과 크게 차이 나지 않도록 하는 것이다. KL divergence가 두 확률 분포인 기존 모델(SFT만 된 모델)의 파라미터를 활용한 확률 분포과 리워드 모델을 활용해 학습 중인 모델의 파라미터를 활용한 확률 분포의 차이를 이용하여 정규화 항으로 사용되고 있기 때문이다.

Direct Preference Optimization

• 위의 RL과정을 보게 되면 3단계로 학습을 진행하게 되고, 또한 외부 리워드 모델이 필요한 것으로 보인다.

• 이러한 과정을 단순화하기 위해서 DPO라는 학습 방법이 나오게 되었다고 생각하면 된다.

• 이에 앞서, RL에서 최종적으로 하고자 했던 것이 무엇이였는지를 먼저 생각해보자.

• RL의 목적은 KL-constrained reward maximization이다. 즉, KL divergence를 통해 어느 정도의 제약을 주면서 보상을 최대화하는 것이 목적이다.

• 그래서 여기서는 RLHF에서의 목적함수를 통해 다음과 같은 식을 보여주고 있다.

  • $\pi_r(y|x) = \frac{1}{Z(x)}\pi_{ref}(y|x)exp(\frac{1}{\beta}r(x,y))$
  • 그렇다면 위의 식은 어떻게 나오게 되었을까?
  • RLHF의 목적함수를 활용하면 다음과 같이 식을 유도할 수 있다.
    
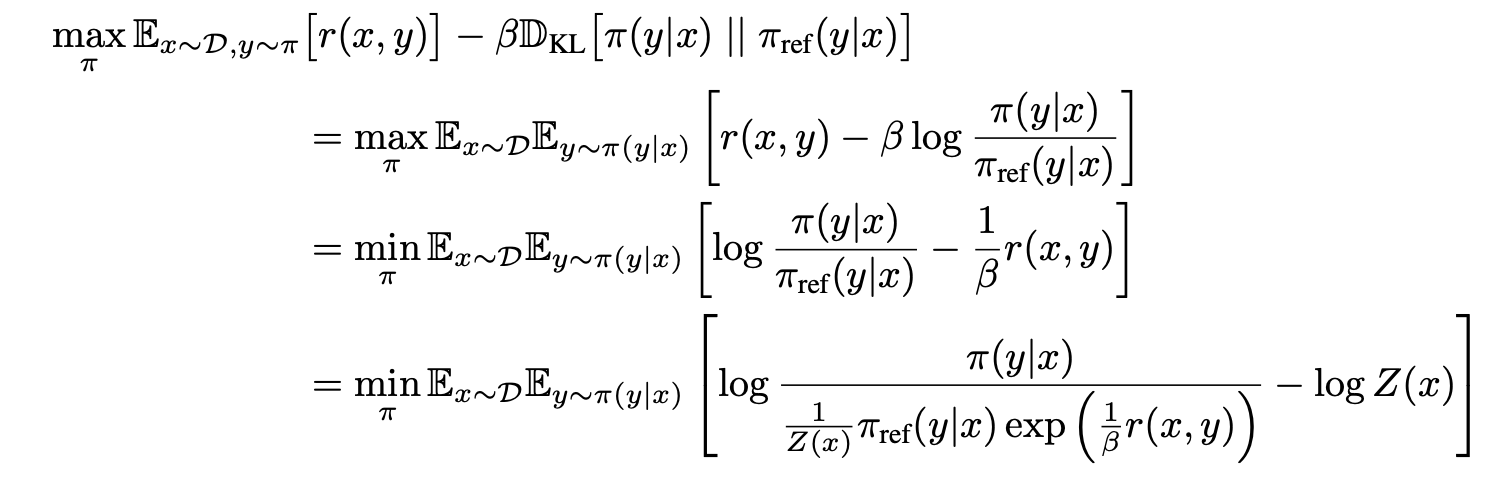
  • 기본적인 식의 유도는 스스로 고민해보면 좋을 것 같다.
  • max에서 min으로 넘어가는 것은 최대화 문제를 최소화 문제로 변환한 것으로 생각하면 된다. max식을 해석해봤을 때, 리워드가 크면서 KL divergence의 값이 작으면 되는데, 이는 반대로 생각하면, KL 다이버전스의 값이 작으면서 리워드가 크면 결국 이게 최소값이 된다는 말이다.

---

위의 식에서부터 최종적으로 DPO의 목적 함수를 유도하기 위한 과정에서 각각의 식들의 의미는 최대한 이해한 바대로 작성한다.(제대로 이해하지 못한 것 같아 아시는 분 계시면 알려주시면 감사하겠습니다!)

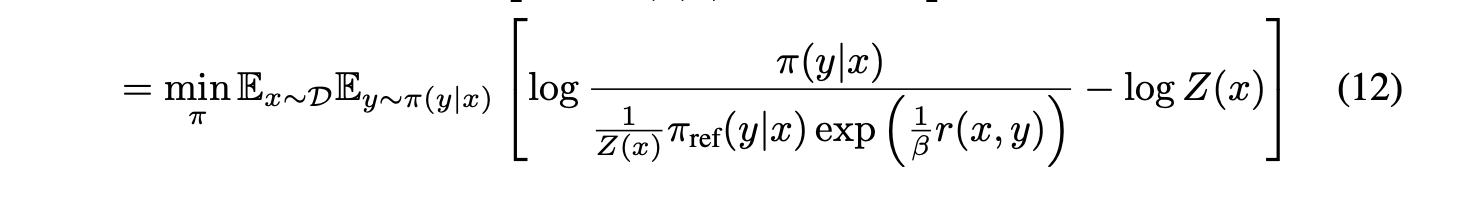
• 위의 식까지 유도된 뒤, direct preference optimization이므로 모델 하나 가지고 바로 최적화를 진행해야 한다. 그러면서도 KL 제약도 있어야하고, 보상도 최대화가 되는 방향으로 나아가야 한다. 그러나 이후 나올 cross entropy loss 방식을 활용하기 위해서는 softmax방식을 차용해야 한다.
• 따라서 $Z(x)$와 같은 형태를 통해 아래 그림이 softmax 형태가 되도록 식을 재구성해주어야 한다.
  
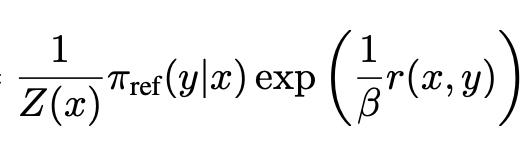
• reference 모델과 보상을 적절한 비율로 최적화시켜야 하는 것이다.
• 그리하여 논문을 보면 최종적으로 DPO의 목적 함수가 다음과 같이 최적화가 된다.
  
• 마지막 식을 보게 되면 KL-divergence가 최소화가 되어야 현재 정책(모델)이 원하는 최적 정책(학습된 모델)이 되므로 최종적인 식은 15번과 같이 된다.
• 직관적으로는 KL 제약이 있는 보상 최대화를 바로 학습할 수 있는 방식으로 식을 재구성했다고 생각하면 된다.

• 그러나 $Z(x)$를 실제로 구하기에는 어려워서 식을 보상함수를 기준으로 재구성한다.
• 그에 따라 나온 식은 다음과 같다.
  • $r(x,y) = \beta \text{log} \frac{\pi_r(y|x)}{\pi_{ref}(y|x)}+ \beta \text{log}Z(x)$
  • 식은 유도해보면 간단히 나온다.
• 우리는 위의 $r$을 어떻게 활용할 것인가를 생각해 보아야 한다.
• RLHF에서 리워드 모델링 파트에서 Bradley-Terry model을 활용하여 preference model을 나타낼 수 있다.
  
• 따라서, 위의 그림에 따라 식을 유도하면 $p^*(y1 > y2|x)$의 식이 유도된다.
• 우리는 이러한 preference 데이터에 대한 확률로 이러한 확률을 구했고, 이를 maximum likelihood objective로 최적화할 수 있는 것이다.
• 그리하여, 최종적으로 아래와 같은 loss함수가 나오는 것이고, 이는 최소화 시키는 것이 목표이다.