[알고리즘] 시간복잡도

sypaik-dev·2023년 9월 29일

Algorithm

목록 보기

1/1

자료구조와 알고리즘, 시간복잡도 대해 공부한 것들을 작성한 글입니다.

알고리즘이란?

알고리즘은 컴퓨터 과학에서 중요한 개념 중 하나로, 문제를 해결하기 위한 방법을 의미한다. 입력 데이터를 처리하여 원하는 결과를 생성하는 데 필요한 지침을 제공하며, 주어진 문제를 해결하는 방법을 명확하게 정의한다.
알고리즘의 효율성은 알고리즘이 입력 데이터에 대해 얼마나 빠르게 동작하는지와 밀접한 관련이 있으며, 이와 관련된 주요 개념 중 하나가 시간복잡도이다.

시간복잡도

알고리즘에서는 문제를 해결하는 것뿐만 아니라 효율적인 방법으로 문제를 해결하는 것도 중요하다. 다시말해 시간복잡도를 고려해야한다.

시간복잡도는 문제를 해결하는데 걸리는 시간과 입력의 함수 관계를 말한다.
입력 크기가 증가하더라도 문제를 해결하는 데 걸리는 시간이 선형적으로 또는 그 이하로 증가하도록 알고리즘이 구성되어야 한다.

시간복잡도 표기 방법

시간 복잡도를 나타내기 위한 표기 방법으로는 크게 3가지가 있다.

Big-O Notation (빅 오 표기법) | 최악의 경우
Big-Ω Notation (빅 오메가 표기법) | 최선의 경우
Big-θ Notation (빅 세타 표기법) | 평균의 경우

이 세가지 중 주로 Big-O 표기법을 사용한다. 이 표기법은 주어진 알고리즘이 얼마나 빨리 실행되는지를 상한으로 제한하여 표현한다.

왜 Big-O 표기법을 사용할까

최선의 경우인 Big-Ω 표기법이나 평균의 경우인 Big-θ 표기법을 사용하지 않고 왜 Big-O 표기법이 널리 사용되는걸까?
왜냐하면 최악의 경우에 대한 보장이 가능하기 때문이다. Big-O 표기법은 알고리즘이 어떤 입력에 대해서도 절대로 더 느리게 실행되지 않을 것임을 보장한다. 따라서 안정성을 보장하고 예측 가능한 성능을 제공하는 데 도움이 된다. 가장 비관적인 상황을 고려하기 때문에 예외적인 경우를 고려하여 시스템을 설계하고 최악의 시나리오에 대비하는 데 도움이 된다.

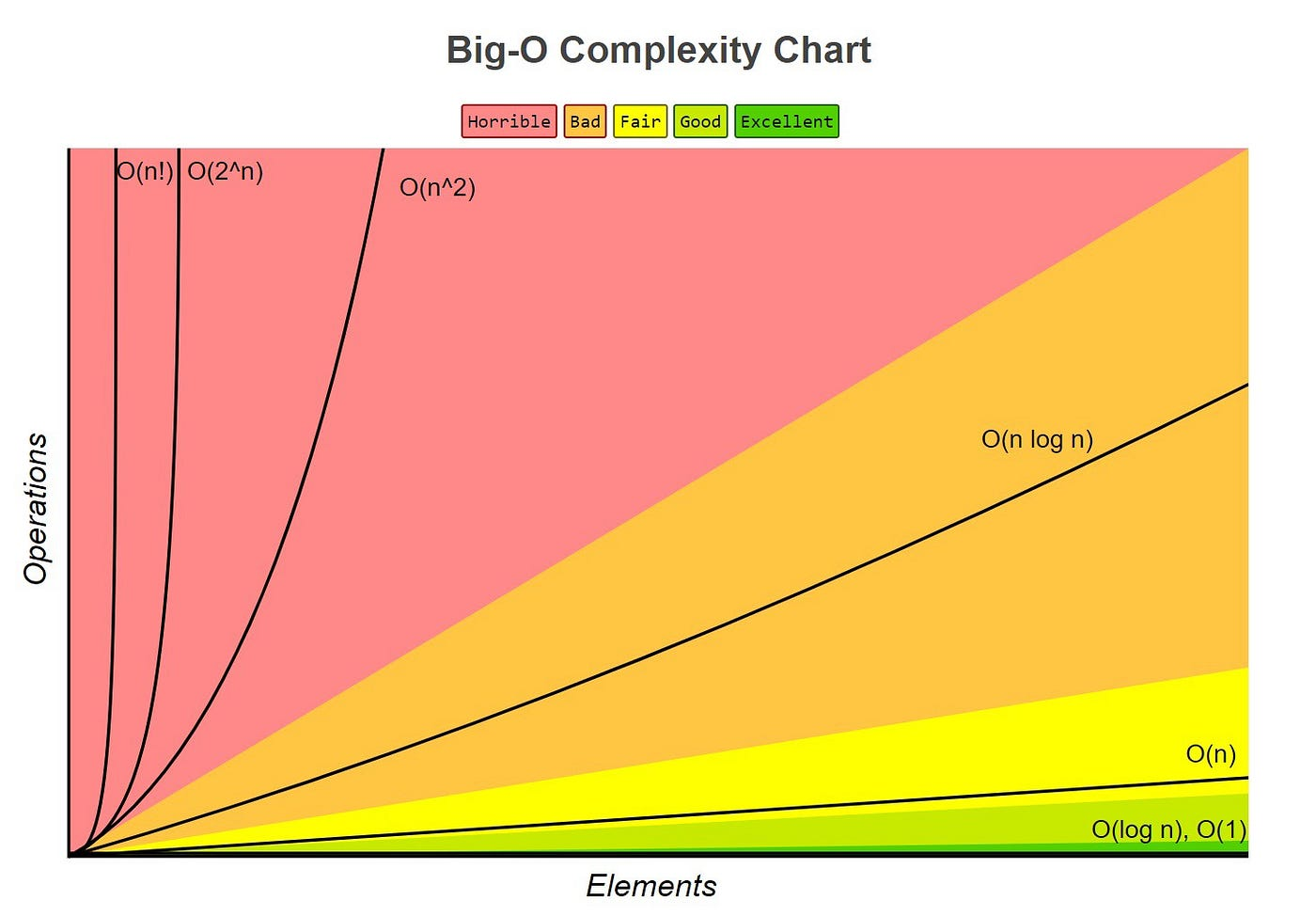
Big-O 표기법이 종류

이미지 출처

1. O(1) - Constant Time

입력크기와 상관없이 항상 일정한 실행 시간을 갖는다.
ex. 배열에서 특정 index의 요소에 접근, 변수에 할당, 산술 연산

def firt_element(arr):
	print(arr[0])

## 입력 크기와 상관없이 항상 1번의 연산만 필요

2. O(n) - Linear Time

입력크기에 비례하여 시간도 같은 비율로 증가한다.
ex. 배열의 모든 요소를 한번씩 검사

def linear_search(arr, target):
	for i in range(len(arr)):
    	if arr[i] == target:
        	return i
            
## 입력 크기에 직선적으로 비례하여 연산이 필요

3. O(log n) - Logarithmic Time

입력 크기에 대해 로그 형태의 실행 시간을 갖는다.
ex. 이진 탐색 알고리즘 (Binary Search)

def binary_search(arr, target):
	left, right = 0, len(arr) - 1
    
    while left<= right:
    	mid = (left + right) // 2
        if arr[mid] == target:
        	return mid
        elif arr[mid] < target:
        	left = mid + 1
        else:
        	right = mid - 1
            
	return -1

## 입력 크기에 대해 로그 시간 복잡도를 가짐

4. O(n^2) - Quadratic Time

입력 크기에 비례하는 실행 시간을 갖는다.
ex. 중첩된 반복문을 사용한 정렬 알고리즘 (버블 정렬, 삽입 정렬)

def bubble_sort(arr):
    n = len(arr)

    for i in range(n):
        for j in range(0, n-i-1):
            if arr[j] > arr[j+1]:
                arr[j], arr[j+1] = arr[j+1], arr[j]

# 입력 크기의 제곱에 비례하는 연산이 필요

5. O(n log n) - Quasilinear Time

입력 크기에 대해 n * log₂(n)에 비례하는 실행 시간을 갖는다.
대용량 데이터를 다루는 정렬 알고리즘에서 많이 쓰인다.
ex. 병합 정렬(merge sort), 퀵 정렬(quick sort)

def merge_sort(arr):
    if len(arr) > 1:
        mid = len(arr) // 2
        left_half = arr[:mid]
        right_half = arr[mid:]

        merge_sort(left_half)
        merge_sort(right_half)

        i = j = k = 0

        while i < len(left_half) and j < len(right_half):
            if left_half[i] < right_half[j]:
                arr[k] = left_half[i]
                i += 1
            else:
                arr[k] = right_half[j]
                j += 1
            k += 1

        while i < len(left_half):
            arr[k] = left_half[i]
            i += 1
            k += 1

        while j < len(right_half):
            arr[k] = right_half[j]
            j += 1
            k += 1

# 입력 크기에 대해 O(n log n) 복잡도를 가짐

6. O(2n) - Exponential Time

입력 크기가 조금만 커져도 기하급수적으로 증가하는 실행 시간을 갖는다.
Big-O 표기법 중 가장 느린 시간 복잡도를 갖는다.
ex. 피보나치 수열을 계산하는 재귀 함수

def fibonacci_recursive(n):
    if n <= 0:
        return 0
    elif n == 1:
        return 1
    else:
        return fibonacci_recursive(n - 1) + fibonacci_recursive(n - 2)

# 입력 크기에 기하급수적인 복잡도를 가짐

sypaik-dev

Frontend Developer