Programmers LV 2

문제 풀이

롤케이크 자르기

from collections import Counter

def solution(topping):
    answer = 0
    cheolsu = Counter(topping)
    brother = {}
    for i in range(len(topping)):
        if topping[i] not in brother:
            brother[topping[i]] = 1
        else:
            brother[topping[i]] += 1
        cheolsu[topping[i]] -= 1
        
        if cheolsu[topping[i]] == 0:
            del cheolsu[topping[i]]
        if len(cheolsu) == len(brother):
            answer += 1
    return answer

< 풀이 과정 >
collections 패키지의 Counter를 이용하여 현재 주어진 topping 들의 각 개수를 세어준다.
이후 철수와 동생을 각 딕셔너리로 구분하여 topping을 for문으로 순회한다.
동생에게 topping이 없다면 1로 채워주고, 있다면 +1 해준 후 철수가 가지고 있는 topping을 1개 빼준다.

만약 그렇게 빼주다가 철수가 가진 토핑 개수가 0이라면 del 처리

마지막으로, 철수와 동생의 키의 길이가 동일하면 answer += 1처리하고 리턴

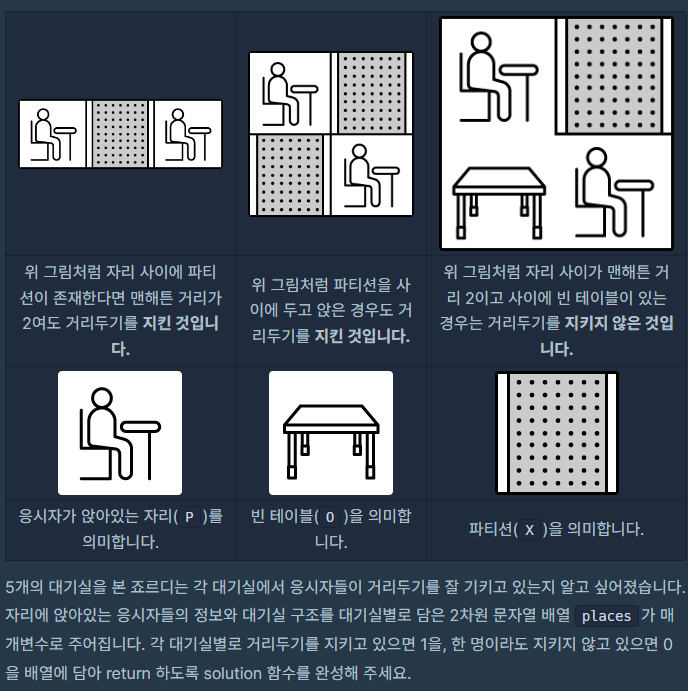
거리두기 확인하기

from collections import deque

def bfs(matrix):
    start = []
    for i in range(5):
        for j in range(5):
            if matrix[i][j] == 'P':
                start.append([i, j])
    for s in start:
        queue = deque([s])
        visited = [[0]*5 for _ in range(5)]
        dist = [[0]*5 for _ in range(5)]
        visited[s[0]][s[1]] = 1
        
        while queue:
            x, y = queue.popleft()
            dx = [-1, 1, 0, 0]
            dy = [0, 0, -1, 1]
            for i in range(4):
                nx = x + dx[i]
                ny = y + dy[i]
                if 0<=nx<5 and 0<=ny<5 and visited[nx][ny] == 0:
                    if matrix[nx][ny] == 'O':
                        queue.append([nx, ny])
                        visited[nx][ny] = 1
                        dist[nx][ny] = dist[x][y] + 1
                    if matrix[nx][ny] == 'P' and dist[x][y] <= 1:
                        return 0
    return 1

def solution(places):
    
    answer = []
    for i in places:
        answer.append(bfs(i))
    return answer   

< 풀이 과정 >
bfs를 활용하여 풀이 진행하였다.
P로 적혀있는 자리는 사람이 앉아있다는 것을 의미하므로, 문제에서 요구하는 '거리두기를 잘 지키고 있는가'를 적용하기 위해 P를 시작점으로 잡았다.
이후 거리와 visit여부를 통해 다음 자리가 P이거나 거리가 0 즉 이동할 수 없는 곳이라면 0을 리턴하고, 다음자리가 빈자리면 queue와 visited처리를 하여 1을 리턴하도록 bfs 알고리즘을 구성하였다.

union - find 예제 (백준)

import sys
sys.setrecursionlimit(10**6)
input = sys.stdin.readline

n, m = map(int, input().split())
parent = [0] * (n+1)
rank = [0] * (n+1)
edges = [[] for _ in range(m+1)]

for i in range(1, n+1):
    parent[i] = i

for i in range(1, m+1):
    a, b, c = map(int, input().split())
    edges[i].extend([c, a, b])

def find(a):
    if parent[a] == a:
        return a
    p = find(parent[a])
    parent[a] = p
    return parent[a]

def union(a, b):
    a = parent[a]
    b = parent[b]
    if a == b:
        return
    if rank[a] > rank[b]:
        parent[b] = a
    else:
        parent[a] = b
        if rank[a] == rank[b]:
            rank[b] += 1


def kruskal(edges):
    edges.sort()
    cost = 0
    mst = []
    for e in edges:
        if not e:
            continue
        c, a, b = e
        if find(a) != find(b):
            union(a, b)
            cost += c
            mst.append([a, b])
            if len(mst) == n-2:
                return cost
    return cost
print(kruskal(edges))