[알고리즘] 백트래킹 (Backtracking)

요즘 학부에서 알고리즘 튜터링을 받고 있는데 (고학번 패스) 알고리즘 알못인 나에게 정말 많은 도움이 되고 있다. 아직 알고리즘 초반이지만 이전에는 그냥 ㅇㅇ납득 이러고 썼던 것을 설계할 줄 알게 되었다고 해야되나..? 중급까지 끝내고 나면 알고리즘 실력이 엄청 많이 늘어있을 것 같다! 그래서 배운 것들을 하나씩 정리해보기로 했다.🔍
+튜터님들이 정말 친절하시고 칭찬을 많이 해주셔서 더 열심히 하고 싶은 마음이 든다ㅎ

백트래킹이란? 🤔

• 완전탐색처럼 모든 경우를 탐색하지만, 탐색 중간에 조건에 맞지 않는다면 가지치기를 통해 탐색 횟수를 줄이는 방법
• 탐색 종료 조건과 언제 가지치기 할 지가 가장 중요함
• 대표적인 완전탐색 방식으로는 DFS(depth-first-search)가 있다.

과정

• 어떤 노드의 유망성 점검
• 유망하지 않다면(non-promising) 가지치기 (pruning)하여 그 전으로 돌아감
  

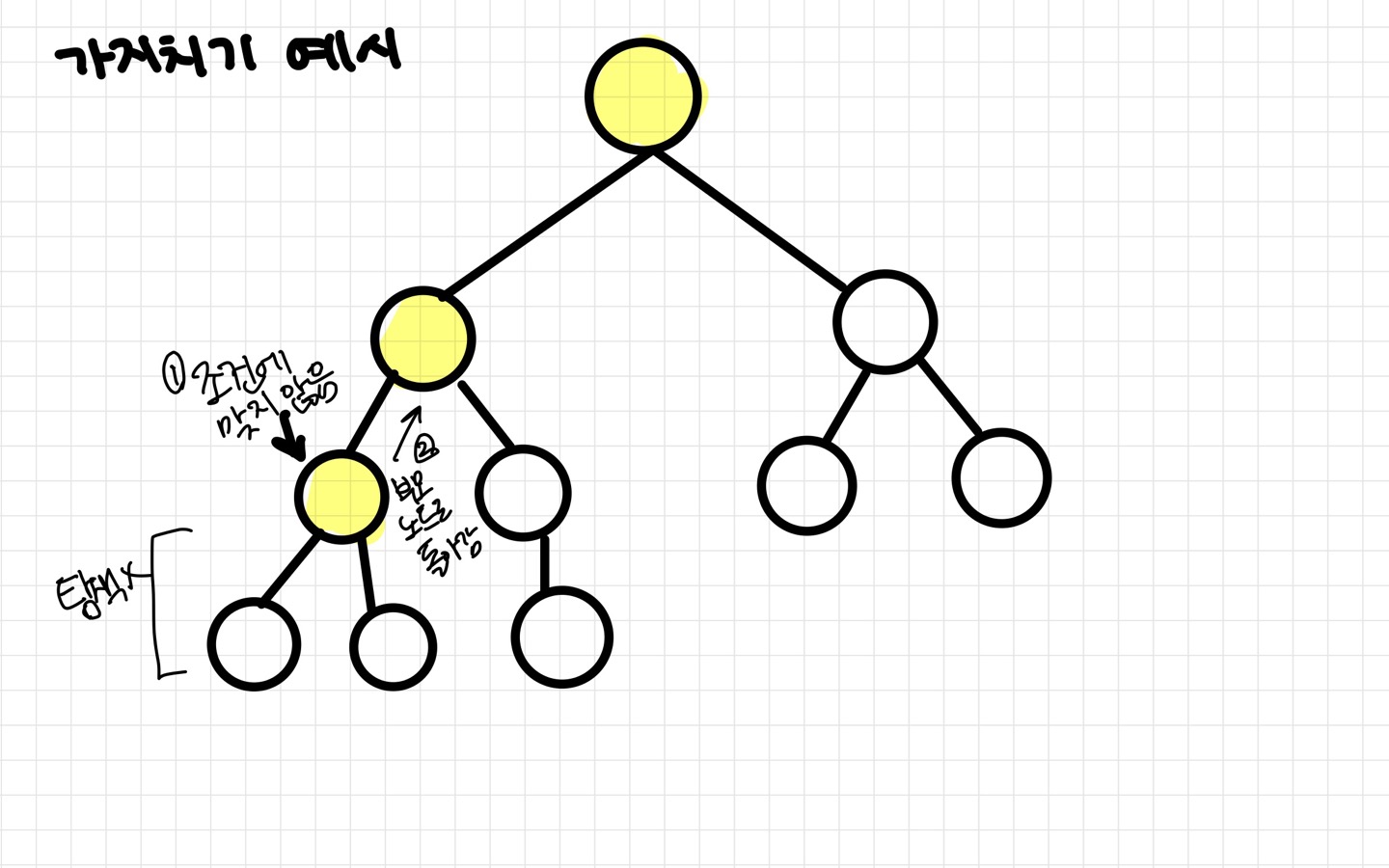
백트래킹으로 푸는 경우

• N의 크기가 작을 때 (보통 20 이하)
• 그 전 과정으로 돌아가면서 탐색해야 하는 경우

예제

백트래킹 예제로는 가장 유명한 N과 M 시리즈가 있다.

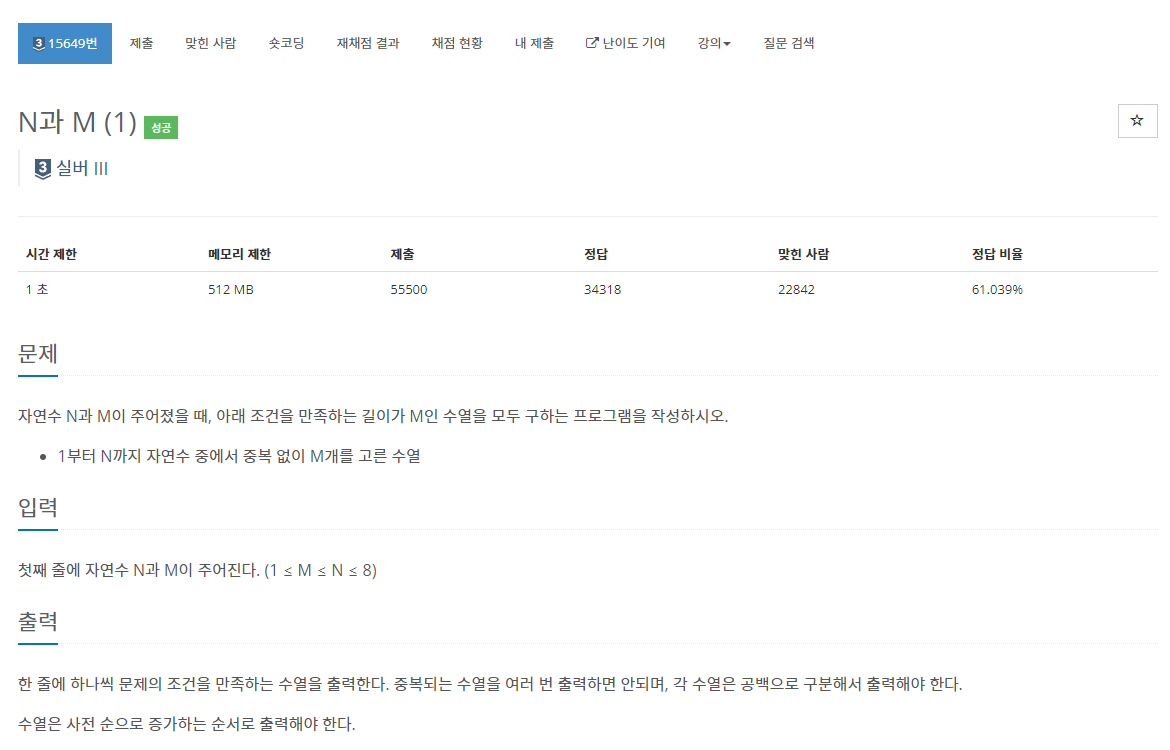
백준 15649 N과 M (1)

접근 💡

• N개 수 중 M개를 중복없이 골라야 함
• 해당 수가 visited되지 않았으면 수열에 넣는다. (중복 제거)
• 탐색 트리의 depth가 M이면 탐색을 종료한다.
• 탐색할 때 visited=true 로 바꾸고 백트래킹을 이어간 후에 다시 visited=false로 돌려놔야 나중에 해당 요소를 재탐색 할 수 있음.

코드 💻

void backtracking(int depth) {
	//M개를 선택했으면 백트래킹 종료 후 출력
	if (depth == M) {
		for (int i = 0; i < M; i++) {
			cout << arr[i] << " ";
		}
		cout << "\n";
	}
	for (int i = 0; i < N; i++) {
		//해당 노드를 방문하지 않았다면 탐색
		if (!visited[i]) {
			visited[i] = true;
			arr[depth] = i + 1;
			backtracking(depth + 1);
			//다시 상태를 돌려 놓음
			visited[i] = false;
		}
	}
}

과제 중 어려웠던 문제 백준 17136 색종이 붙이기

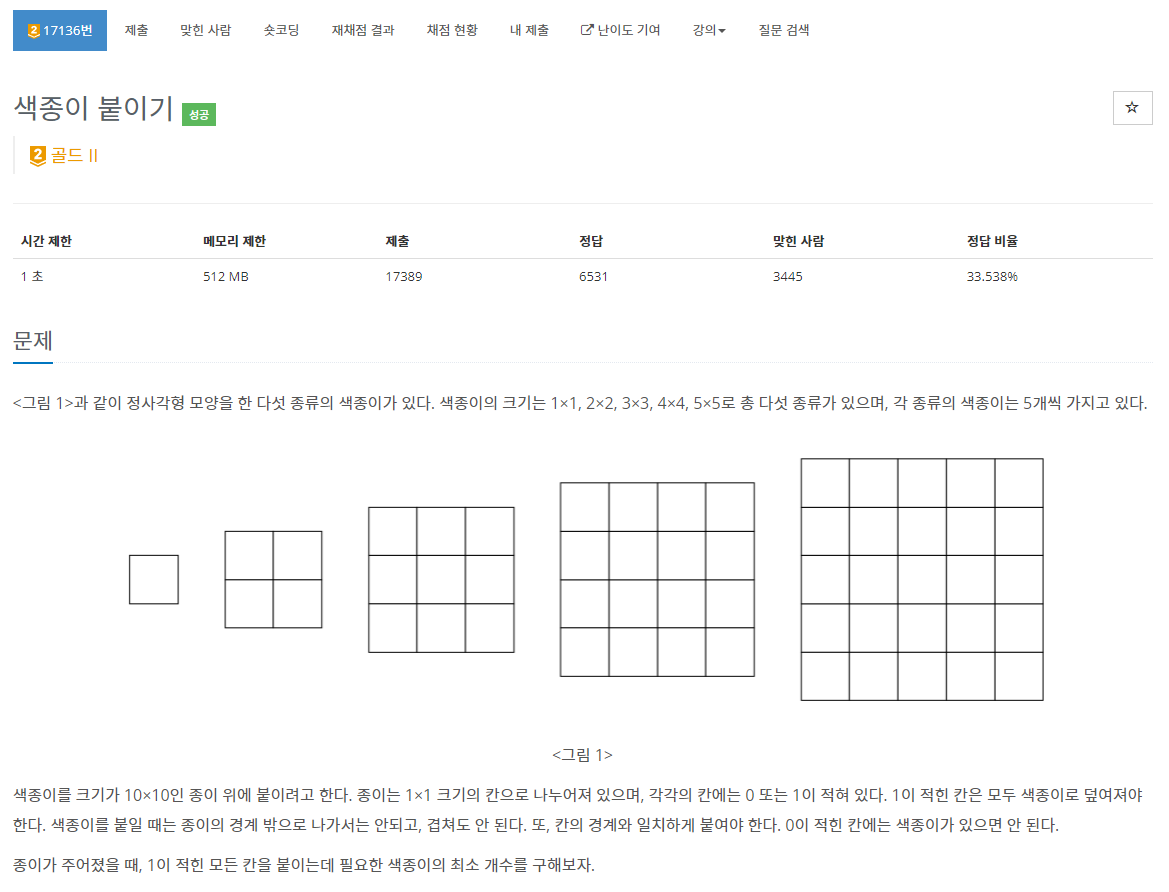
무려 골드2의 문제였다..! 처음에는 무조건 가장 큰 색종이를 붙이면 되지 않나 했는데 5*5를 붙이고 짜투리때문에 작은 색종이를 많이 붙이는 경우도 있어서 모든 해를 탐색하고 최소값을 구해야 했다.

접근 💡

• (x,y) 좌표에서 n*n 사이즈의 색종이를 붙일 수 있는지 확인
• 붙일 수 있다면 붙인 뒤에 탐색을 계속하고 다시 뗀다.
• 만약 색종이 개수가 최소값이 될 수 없는 경우 종료
• 마지막 타일에 도달한 경우 종료하고 답 갱신

코드 💻

1. (x,y)에서 시작하여 n*n 사이즈 색종이를 붙일 수 있는지 확인하는 함수

bool isStickable(int x, int y, int n) {
	for (int i = x; i < x + n; i++) {
		for (int j = y; j < y + n; j++) {
			if (v[i][j] == 0) return false;
		}
	}
	return true;
}

2. 색종이를 붙였다 떼는 함수

void stick(int x, int y, int n, int attached) {
	for (int i = x; i < x + n; i++) {
		for (int j = y; j < y + n; j++) {
			v[i][j] = attached;
		}
	}
}

3. 탐색

void backtracking(int x, int y, int cnt) {
	//종료조건
	//더이상 최소값이 나올 수 없을 때
	if (cnt > answer) return;
	if (x > 9) {
		answer = min(answer, cnt);
		return;
	}
	//옆으로 더 탐색할 수 없을 때
	if (y > 9) {
		backtracking(x + 1, 0, cnt);
		return;
	}

	if (v[x][y] == 0) {
		backtracking(x, y + 1, cnt);
		return;
	}

	if (v[x][y] == 1) {
		for (int i = 1; i <= 5; i++) {
			if (x + i > 10 || y + i > 10 || paper[i - 1] == 0) continue;
			if (isStickable(x, y, i)) {
				stick(x, y, i, 0);
				paper[i - 1]--;
				backtracking(x, y + 1, cnt+1);
				stick(x, y, i, 1);
				paper[i - 1]++;
			}
		}
	}
}

이렇게 더이상 유망하지 않다고 판단되는 노드를 가지치기를 통해 탐색 시간을 줄이는 것이 백트래킹 알고리즘이다.