베이지안 네트워크 Bayes network

= 신뢰 네트워크, 의사결정 네트워크

확률변수 간의 조건부 의존성을 표현하는 Directed Acyclic Graph (DAG, 방향성 비순환 그래프) 기반 모델

변수 시퀀스를 모델링하는 베이지안 네트워크는 동적 베이지안 네트워크

node 확률변수
관찰 가능한 양, 잠재변수, 가설 (연결 안 된 노드는 조건부로 서로 독립적인 변수)
edge 조건부 종속성, 인과관계
CPT 조건부 확률표

베이지안 확률

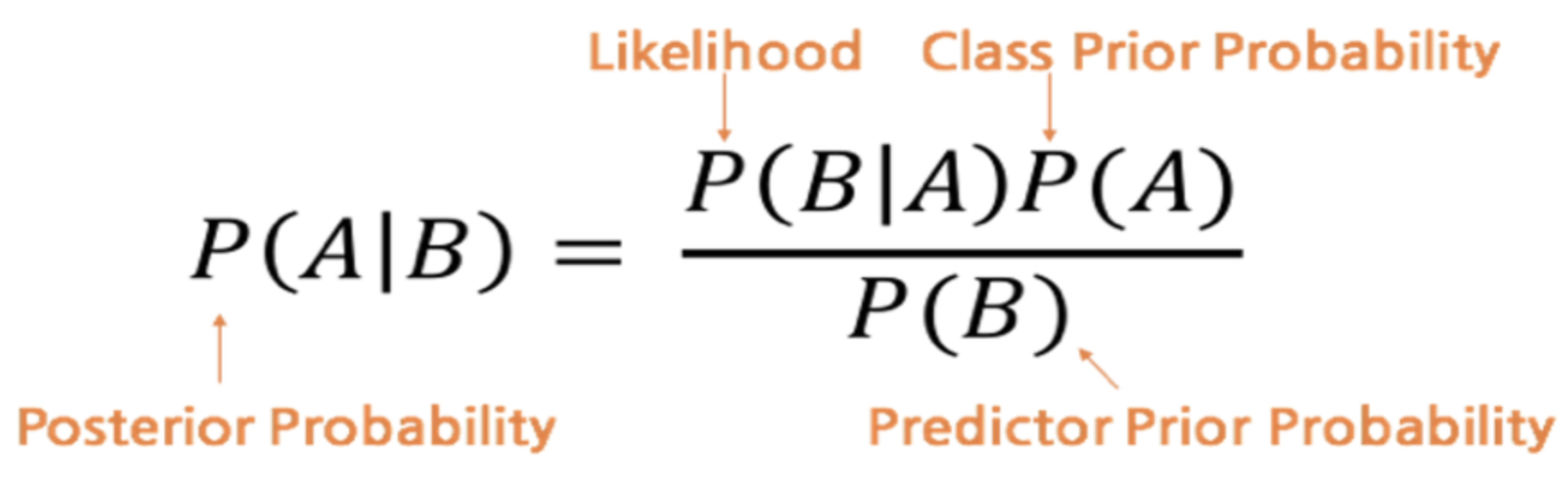
📘 베이지안 네트워크 학습 방법

🧩 1. 구조 학습 (Structure Learning)

✅ 개념:
변수 간의 조건부 독립성을 파악해서 그래프 구조(DAG)를 찾는 과정이야.

어떤 노드와 어떤 노드가 연결되어 있는지를 찾는 거지.

DAG(방향성 비순환 그래프)의 형태를 결정함.

✅ 접근 방식:
점수 기반 방법 (Score-based)

후보 구조들을 생성한 뒤, 각 구조에 대해 스코어(적합도)를 계산하고 가장 높은 점수를 가진 구조를 선택

대표적인 스코어 함수:

BIC (Bayesian Information Criterion)

AIC (Akaike Information Criterion)

Bayesian score (BDe score)

제약 기반 방법 (Constraint-based)

조건부 독립성 테스트를 이용해서 변수 간의 관계를 추론

예시: PC 알고리즘

하이브리드 방법

점수 기반 + 제약 기반 혼합

🧮 2. 모수 학습 (Parameter Learning)

✅ 개념:
구조가 정해졌을 때, 각 노드의 조건부 확률표(CPT)를 채우는 과정이야.

즉, 예를 들어 P(기침|감기) 이런 확률값을 학습하는 거지.

✅ 방법:
최대우도추정 (MLE, Maximum Likelihood Estimation)

데이터에서 가장 일어날 법한 확률값을 선택

단순히 관측된 데이터의 비율로 확률을 계산

예시: 감기인 경우 기침한 횟수 / 감기인 총 횟수

베이지안 추정 (Bayesian Estimation)

사전확률(prior)을 설정해서 불확실성을 반영

데이터가 적어도 안정적인 추정을 가능하게 해줌

주로 디리클레 분포(Dirichlet distribution)를 사전 분포로 사용

🎯 예시 정리
감기 여부(G) → 기침 여부(C)

구조 학습: G → C 라는 DAG 구조를 도출

모수 학습 (MLE):

감기 O일 때 기침 O: 30번 / 감기 O 총 40번 → P(C=O|G=O) = 0.75

감기 X일 때 기침 O: 10번 / 감기 X 총 60번 → P(C=O|G=X) = 0.166

---

✅ 1. 구조 학습 알고리즘
베이지안 네트워크에서 어떤 노드들이 연결될지(즉, 그래프 구조)를 자동으로 정하는 방법이야.

📌 대표 알고리즘 2가지
🔹 점수 기반 (Score-Based)
가능한 모든 DAG를 만들어보고, 점수가 가장 높은 구조 선택

점수 기준

• BIC (Bayesian Information Criterion)
• AIC (Akaike Information Criterion)
• BDe score (Bayesian Dirichlet equivalent score)
• Hill Climbing 알고리즘이 자주 쓰임
  : 지금 구조에서 조금씩 간선을 바꿔가며 점수 좋은 구조로 "등산"하듯이 이동

🔹 제약 기반 (Constraint-Based)
변수들 간의 조건부 독립성 테스트를 통해 관계를 결정

PC 알고리즘이 대표적
독립이면 → 연결 안 함
독립이 아니면 → 연결함

✅ 2. MLE vs Bayesian 추정 (모수 학습 방법)
🟦 MLE (Maximum Likelihood Estimation)
관측값 기반 단순 비율로 확률 계산

수식

𝑃(𝑋∣𝑌) = Y일 때 X가 나온 횟수 / Y가 나온 전체 횟수
P(X∣Y)= Y가 나온 전체 횟수 / Y일 때 X가 나온 횟수

예시
유저가 감기일 때 기침한 횟수 = 30
감기인 경우 총 횟수 = 40

$P(\text{기침} \mid \text{감기}) = \frac{30}{40} = 0.75$

🟦 Bayesian Estimation
사전확률(prior)을 추가로 고려
적은 데이터에서도 안정적인 확률 추정 가능
디리클레 분포를 사전분포로 사용함

수식
$P(X \mid Y) = \frac{n_{XY} + \alpha}{n_Y + k\alpha}$

예시
$P(\text{기침=Yes} \mid \text{감기}) = \frac{30 + 1}{40 + 2} = \frac{31}{42} \approx 0.738$

✅ 요약 비교표

항목	MLE	Bayesian
사전지식	없음	있음 (사전확률)
데이터 적을 때	불안정	안정적
수식	단순 비율	smoothing 적용
장점	빠르고 직관적	과적합 방지, 정교함