[BaekJoon] 9613 GCD 합

1.  문제 링크

2.  문제

요약

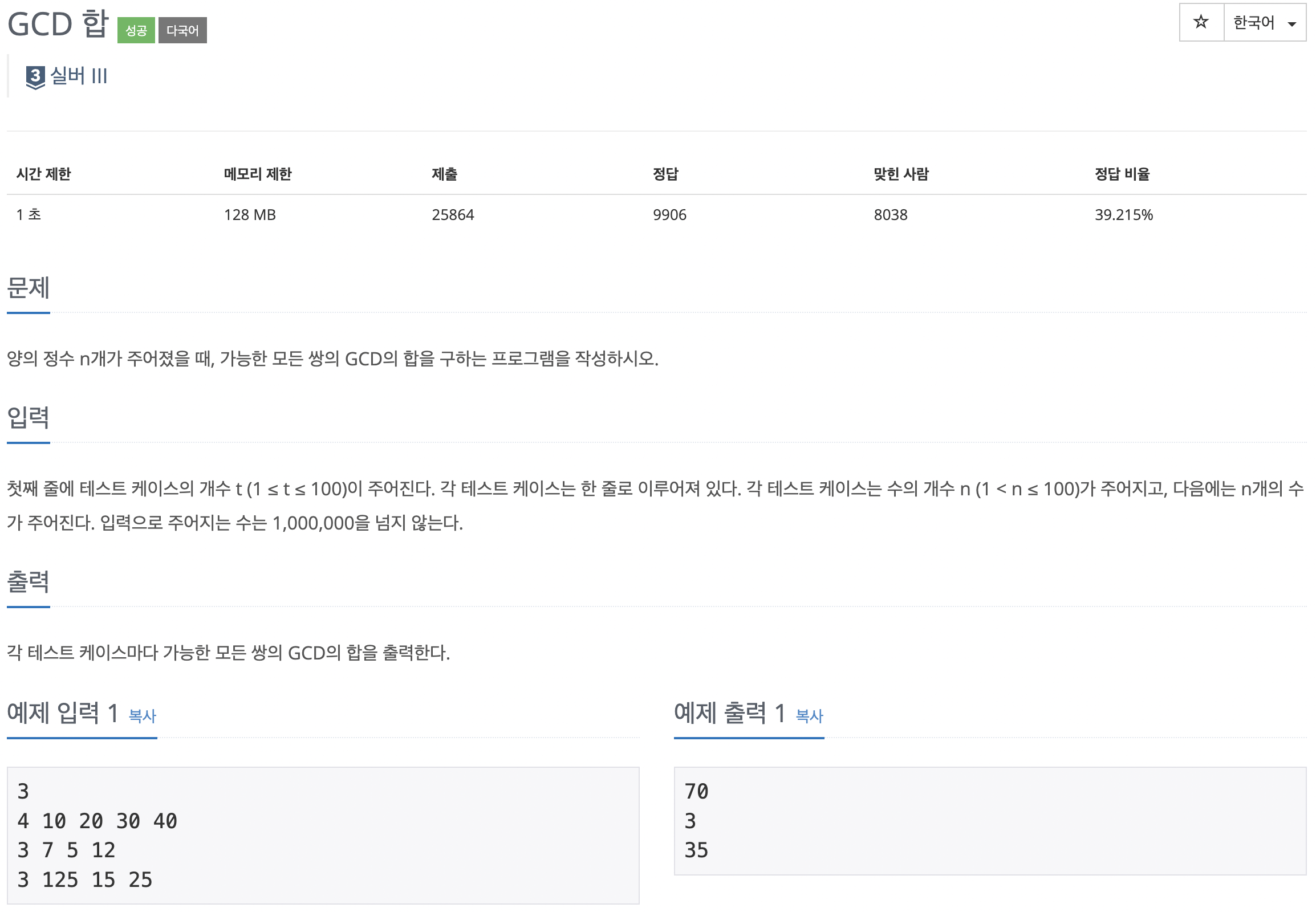
• 양의 정수가 n개 주어졌을 때, 가능한 모든 쌍의 GCD의 합을 구하는 문제입니다.
• 입력
• 첫 번째 줄에 테스트 케이스의 개수가 주어지고 두 번째 줄부터 n개의 줄에 각 테스트 케이스가 주어집니다.
• 각 테스트 케이스에서는 테스트 케이스에서의 수의 개수가 우선 주어지고 이후 n개의 수가 주어집니다.
• 출력: 각 테스트 케이스에서 가능한 모든 쌍의 GCD의 합을 테스트 케이스 순서대로 출력합니다.

3.  소스코드

import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.StringTokenizer;

public class Main {
	public int gcd(int a, int b) {
		if(b == 0) {
			return a;
		} else {
			return gcd(b, a % b);
		}
	}
	
	public long[] getGCDSum(String[] testcase) {
		long[] result = new long[testcase.length];
		for(int i = 0; i < testcase.length; i++) {
			StringTokenizer st = new StringTokenizer(testcase[i]);
			int num = Integer.parseInt(st.nextToken());
			int[] nums = new int[num];
			for(int j = 0; j < num; j++) {
				nums[j] = Integer.parseInt(st.nextToken());
			}
			long sum = 0;
			int gcd = 0;
			for(int j = 0; j < nums.length - 1; j++) {
				for(int k = j + 1; k < nums.length; k++) {
					if(nums[j] < nums[k]) {
						gcd = gcd(nums[k], nums[j]);
					} else {
						gcd = gcd(nums[j], nums[k]);
					}
					sum += gcd;
				}
			}
			result[i] = sum;
		}
		return result;
	}
	
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
		int test_num = Integer.parseInt(br.readLine());
		String[] testcase = new String[test_num];
		for(int i = 0; i < test_num; i++) {
			testcase[i] = br.readLine();
		}
		br.close();
		Main m = new Main();
		long[] result = m.getGCDSum(testcase);
		for(int i = 0; i < result.length; i++) {
			bw.write(result[i] + "\n");
		}
		bw.flush();
		bw.close();
	}
}

4.  접근

• 각 테스트 케이스에서 주어진 수들에 대해 가능한 쌍들을 모두 찾고 그 쌍들에 대해서 최대공약수를 구해 모두 더해주면 되는 문제입니다.
• 최대공약수를 구할 때는 유클리드 호제법을 이용하여 구하기 때문에 쌍을 이룬 두 수 중에서 큰 수가 첫 번째 매개변수 자리에 들어가고 다른 수가 두 번째 매개변수 자리에 들어갑니다.
• 유클리드 호제법을 이용하여 구한 최대공약수들을 모두 더하여 가능한 쌍들의 GCD의 합을 구하고 이를 모든 테스트 케이스에 대해 수행하여 결과를 냅니다.