자료구조 정리

자료구조란

자료구조는 데이터를 원하는 규칙 또는 목적에 맞게 저장하기 위한 구조이고, 알고리즘이란 자료구조에 쌓인 데이터를 활용해 어떠한 문제를 해결하기 위한 여러 동작들의 모임이다.

ArrayList / LinkedList

배열 (ArrayList)

• 여러 데이터를 하나의 이름으로 그룹핑해서 관리 하기 위한 자료구조로 index와 값의 쌍으로 구성되어있다.
• 연속된 메모리의 공간으로 이루어져 있다
• 배열은 정의와 동시에 길이를 지정하며 길이를 바꿀 수 없다.
• 크기가 고정되어 있기 때문에 어떤 엘리먼트가 삭제되면, 삭제된 상태를 빈 공간으로 남겨두어야 한다. => 메모리 낭비
• ArrayList는 Random Access를 지원한다. 인덱스로 바로 접근할 수 있기 때문에 특정 요소를 접근하기 위해서는 O(1)의 시간이 필요하다.
• 삽입과 삭제에 대해서는 요소를 모두 옮겨주어야 하기 때문에 O(N)의 시간이 필요하다.
• 스택을 구현하기 좋다. LinkedList로 구현하게 되면 객체를 제거하는 작업이 필요하지만 ArrayList로 구현하게 되면 index를 줄이고 초기화만 하면 된다.

연결리스트(LinkedList)

• 연결리스트란 먼저 각 노드가 데이터와 포인터를 가지고 한 줄로 연결되어 있는 방식으로 데이터를 저장하는 자료구조이다.
• 각 노드는 해당하는 데이트를 갖고 있고 포인터를 통해 다음 노드의 주소값을 저장하고 있다.
• 링크드 리스트는 Sequential Access를 지원한다. 각 노드가 다음 포인터의 주소를 갖고 있기 때문에 특정 요소에 접근하기 위해서는 O(N)의 시간이 필요하다.
• 링크드 리스트는 노드가 저장하고 있는 주소값을 바꿔주면 되기 때문에 삽입과 삭제에는 O(1)의 시간이 소요된다.

  배열에서 메모리는 선언 시 컴파일 타임에 할당이 된다.(정적 메모리 할당) 반면 Linkedlist에서는 새로운 요소가 추가될 때 런타임에 메모리를 할당한다.(동적 메모리 할당)

• 한 개의 Node는 다른 Node에 대한 참조만 가지고 있다. 따라서 공간적 제약을 ArrayList에 비해 받지 않는다
• 배열은 Stack 섹션에 메모리 할당이 이루어 진다. 반면 Linkedlist는 Heap 섹션에 메모리 할당이 이루어진다.
• 큐를 구현하기 좋다. 삽입과 삭제가 용이하기 때문에 삭제하게 되면 모든 요소를 앞으로 이동시켜야 하는 ArrayList보다 LinkedList가 좋다.

스택 & 큐

스택

• LIFO(Last In First Out)으로 가장 나중에 들어온 것이 가장 먼저 나간다. 세로로 된 통이라고 생각하면 된다.
• 스택은 정해진 방향으로만 쌓을수 있고, top으로 정한 곳을 통해서만 접근할 수 있다.
• 스택에서 top을 통해 삽입하는 연산을 'push' , top을 통한 삭제하는 연산을 'pop'이라고 한다.
• 비어있는 스택에서 원소를 추출하려고 할 때 stack underflow라고 하며, 스택이 넘치는 경우 stack overflow라고 한다.

큐

• FIFO(First In First Out)으로 가장 먼저 들어온 것이 먼저 나간다. 가로로 된 통과 같은 구조라고 생각하면 된다.
• 삭제연산만 수행되는 곳을 프론트(front), 삽입연산만 이루어지는 곳을 리어(rear)로 정하여 각각의 연산작업만 수행된다.
• 큐의 리어에서 이루어지는 삽입연산을 인큐(enQueue) 프론트에서 이루어지는 삭제연산을 디큐(dnQueue)라고 부른다.

스택 두개로 큐를 구현하는 방법은 ??

스택 하나는 입력용 하나는 출력용으로 두면 된다.
하나의 스택에 계속 입력을 받다가 pop()을 하게 되면 출력용 스택이 비어있을 경우에만 입력용 스택의 모든 원소를 두번째 출력용 스택으로 거꾸로 넣고 하나씩 빼주면 된다. 만약 출력용 스택이 비어있지 않다면 그대로 빼주면 된다.

그래프, 트리, 트라이

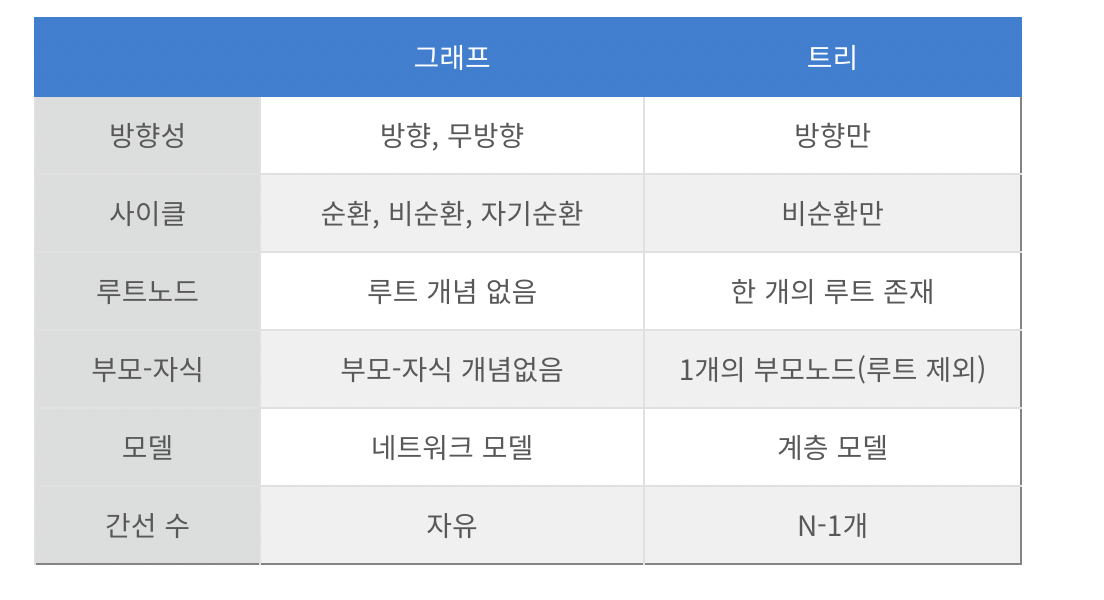
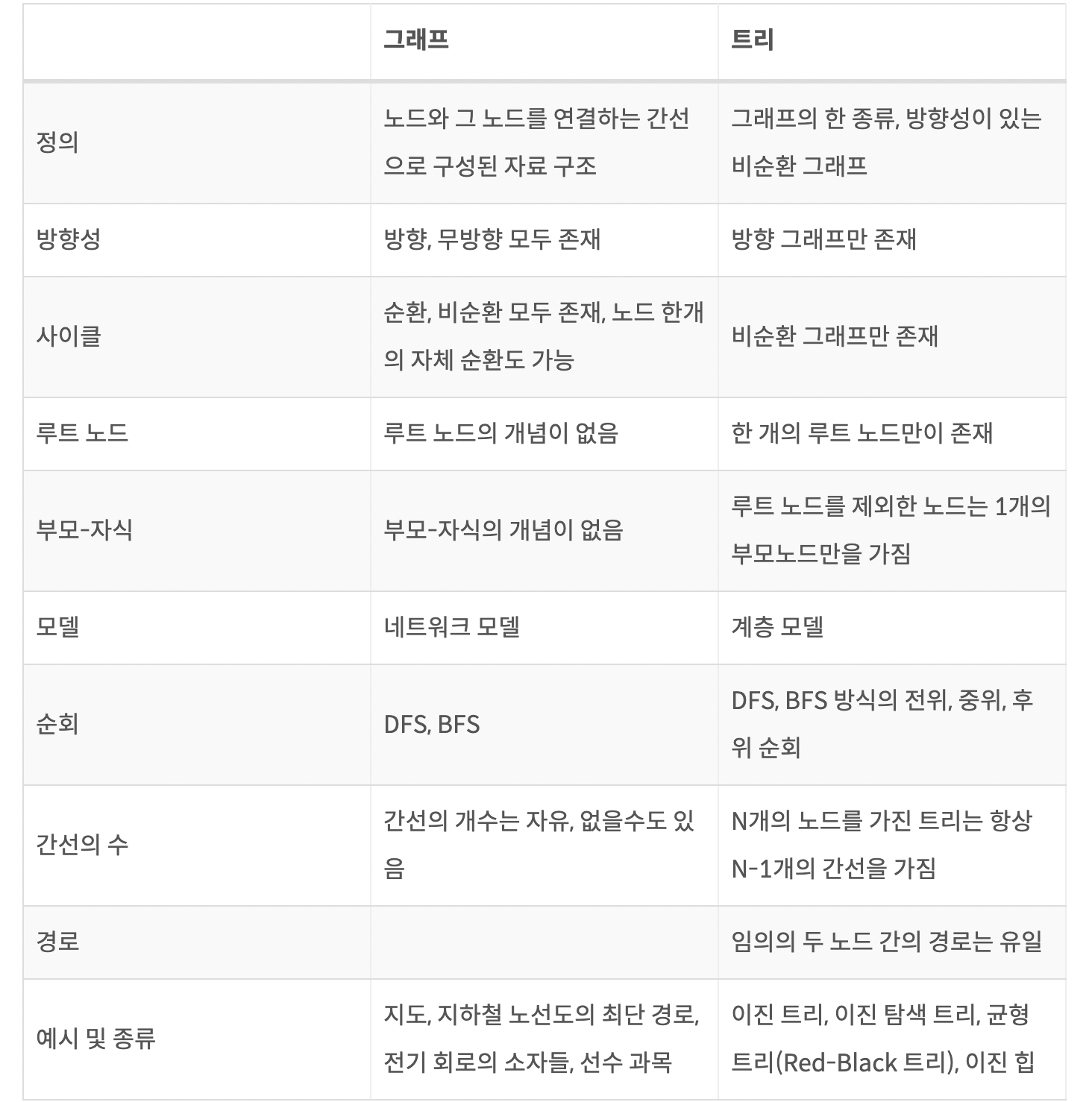
그래프

• 그래프는 노드(하나의 점)와 노드 간을 연결하는 간선으로 구성된 자료 구조이다. 이를 통해 연결된 노드 간의 관계를 표현할 수 있는 자료구조이다.
• 그래프는 순환 혹은 비순환 구조를 이룬다
• 그래프는 방향이 있는 그래프와 방향이 없는 그래프가 있다.
• 루트 노드의 개념이 없다 / 부모-자식 관계라는 개념이 없다.
• 2개 이상의 경로가 가능하다.(무방향, 방향, 양방향 가능)
• 그래프는 네트워크 모델이다.

트리

• 트리는 그래프와 같이 노드와 노드간을 연결하는 간선으로 구성된 자료구조이다.
• 트리는 두 개의 노드 사이에 반드시 1개의 경로만을 가지며 사이클이 존재하지 않는 방향 그래프이다.
• 부모-자식 관계가 성립하기 때문에 계층형 모델이라고도 한다.

트라이

• 트라이(Trie)는 문자열을 저장하고 효율적으로 탐색하기 위한 트리 형태의 자료구조이다.

• 우리가 검색할 때 볼 수 있는 자동완성 기능, 사전 검색 등 문자열을 탐색하는데 특화되어있는 자료구조라고 한다.

• 래딕스 트리(radix tree) or 접두사 트리(prefix tree) or 탐색 트리(retrieval tree)라고도 한다. 트라이는 retrieval tree에서 나온 단어이다.

• 예를 들어 'Datastructure'라는 단어를 검색하기 위해서는 제일 먼저 'D'를 찾고, 다음에 'a', 't', ... 의 순서로 찾으면 된다. 이러한 개념을 적용한 것이 트라이(Trie)이다.

• 트라이(Trie)는 문자열 검색을 빠르게 한다.

• 문자열을 탐색할 때, 하나하나씩 전부 비교하면서 탐색을 하는 것보다 시간 복잡도 측면에서 훨씬 더 효율적이다.

• 각 노드에서 자식들에 대한 포인터들을 배열로 모두 저장하고 있다는 점에서 저장 공간의 크기가 크다는 단점도 있다. (메모리 측면에서 비효율적일 수 있음!)

자세한 참고 : 트라이 관련 벨로그

힙(Heaps)

• 완전 이진 트리를 기초로 하고 우선순위 큐를 위하여 만들어진 자료구조.
  • 완전 이진트리는 마지막을 제외한 모든 노드에서 자식들이 꽉 채워진 이진트리를 말한다.
• 여러 개의 값들 중에서 최댓값이나 최솟값을 빠르게 찾아내도록 만들어진 자료구조
• 힙에서의 부모 노드와 자식 노드의 관계
  • 왼쪽 자식의 인덱스 = (부모의 인덱스) * 2
  • 오른쪽 자식의 인덱스 = (부모의 인덱스) * 2 + 1
  • 부모의 인덱스 = (자식의 인덱스) / 2

해시테이블

• 해시 테이블은 (Key, Value)로 데이터를 저장하는 자료구조 중 하나로 빠르게 데이터를 검색할 수 있는 자료구조
• 해시 테이블이 빠른 검색속도를 제공하는 이유는 내부적으로 배열(버킷)을 사용하여 데이터를 저장하기 때문이다.
• 해시 테이블은 각각의 Key값에 해시함수를 적용해 배열의 고유한 index를 생성하고, 이 index를 활용해 값을 저장하거나 검색하게 된다. 여기서 실제 값이 저장되는 장소를 버킷 또는 슬롯이라고 한다.

ex) ('taehong','software')라는 (Key,Value)가 들어오면 taehong을 해시함수에 돌린 결과값이 index에 들어가게 된다. index=hashFuc('taehong')이 되고 이 index를 통해 buckets[index]='software' 로 정보를 저장하게 된다. 따라서 해시함수를 통해 나온 결과값을 index로 접근하기 때문에 시간복잡도는 O(1)이 된다.

해시 값이 충돌할 경우

결국 데이터가 많아지면, 다른 데이터가 같은 해시 값으로 충돌나는 현상이 발생함 'collision' 현상
서로 다른 인풋에 대해 해시 함수를 돌려서 나온 결과값이 동일하다면 해당하는 인덱스에 값이 충돌하게 된다. 이러한 경우에는 분리 연결법(Separate Chaining)과 개방 주소법(Open Addressing) 두가지로 크게 해결하고 있다.

분리 연결법(Separate Chaining)

• Separate Chaining이란 동일한 버킷의 데이터에 대해 링크드 리스트를 활용하여 메모리를 사용하여 다음 데이터의 주소를 저장하는 것이다.
• 이 방법을 사용하게 되면 테이블을 확장할 필요 없이 간단하게 구현 가능하며 위에서 말했듯이 링크드 리스트를 사용하였기 때문에 삽입과 삭제가 편하다는 장접이 있다.
• 하지만 충돌되는 데이터가 많아지면 chaning되는 데이터가 많아져 캐시의 효율이 감소한다. 연결 리스트로 인해 최악의 경우 수행 시간이 O(n)이 된다. 해시를 사용하는 이유는 O(1)이라는 장점으로 사용하는 것인데 O(n)이 된다면 문제가 된다.

개방 주소법(Open Addressing)

추가적인 메모리를 사용하는 Chaining 방식과 다르게 비어있는 해시 테이블의 공간을 활용하는 방법이다. 대표적인 방법은 3가지가 있다.
1. 선형 프로빙(Linear probing)
현재의 버킷 index로부터 고정폭 만큼씩 이동하여 차례대로 검색해 비어 있는 버킷에 데이터를 저장한다.
primary clustering는 한 번 충돌이 나면 집중적으로 충돌이 발생하는 것을 의미한다. 이로 인하여 평균 검색 시간이 증가한다.
2. 이차식 프로빙(Quadratic probing)
시의 저장순서 폭을 제곱으로 저장하는 방식이다. 예를 들어 처음 충돌이 발생한 경우에는 1만큼 이동하고 그 다음 계속 충돌이 발생하면 2^2, 3^2 칸씩 옮기는 방식이다.
secondary clustering은 처음 충돌한 위치가 같다면 다음 충돌할 위치도 반복적으로 계속 충돌이 나게 된다는 의미이다.
3. 이중 해시(Double hasing)
해시된 값을 한번 더 해싱하여 해시의 규칙성을 없애버리는 방식이다. 해시된 값을 한번 더 해싱하여 새로운 주소를 할당하기 때문에 다른 방법들보다 많은 연산을 하게 된다.

참고할만한 자료

• [자료구조] 면접질문 모음