[Algorithm] 정렬 알고리즘

Mintaek·2023년 11월 23일
algorithm
0

Algorithm study

목록 보기
3/3
post-thumbnail

정렬 알고리즘

정렬 알고리즘이란 ? 데이터 요소를 특정 순서로 나열하는 알고리즘.

  • 필요한 이유
    • 데이터를 효과적으로 검색하거나 효율적으로 처리하기 위해서.
    • 데이터 검색 속도 향상
    • 데이터 비교와 교환 횟수 최소화

정렬 알고리즘은 데이터를 특정 순서로 나열하는 데 사용되며, 위와같이 다양한 측면에서 유용하다. 정렬 알고리즘의 종류를 알아보기 전에 두 가지 주요한 정렬 특성인 stable정렬과 in-place 정렬에 대해 알아보자.

Stable 정렬과 In-place 정렬

Stable 정렬

  • 정렬했을 때 중복된 값들의 순서가 변하지 않는 것을 의미한다.
  • 정렬된 데이터의 안정성을 보장한다.
  • 여러 정렬 조건이 있는 경우 유용하다.
// stable 정렬 예시
let numbers = [1,4(첫번째),5,2,3,4(두번째)]

// 문자열을 기준으로 정렬
numbers.sort();
console.log(numbers) 

// 결과
[ 1, 2, 3, 4(첫번째), 4(두번째), 5 ]

In-place 정렬

  • 추가적인 메모리 공간이 거의 들지 않는 정렬.
  • 메모리 효율성이 중요한 경우 사용된다.
  • 주어진 데이터 배열 내에서 요소의 위치를 변경하면서 정렬을 수행한다.

1. 버블 정렬 (Bubble Sort)

옆에 있는 데이터와 비교하여 더 작은 값을 앞으로 보내는 정렬. 즉, 가장 큰 값이 맨 뒤로 간다. 정렬 방식이 마치 물속에서 올라오는 물방울과 같다고하여 버블 정렬이라고 한다.

버블정렬

구현

function bubbleSort(arr) {
  for (let i = 0; i < arr.length; i++) {
    for (let j = 1; j < arr.length; j++) {
      if (arr[j - 1] > arr[j]) {
        [arr[j - 1], arr[j]] = [arr[j], arr[j - 1]];
      }
    }
  }
  return arr;
}
console.log(bubbleSort([1, 4, 3, 6, 5])) // [ 1, 3, 4, 5, 6 ]

장점

  • 앞뒤 비교하여 큰 수를 뒤로보내는 간단한 작업. 그러므로 구현이 매우 쉽다.
  • 주어진 데이터 배열 내에서 요소의 위치를 변경하므로 In-place 정렬이다.
  • Stable 정렬.

단점

  • 두 원소를 한 번씩 비교해서 정렬하므로 매우 비효율적이다.
  • 시간 복잡도가 최악,최선,평균 모두 O(n^2)이다.
  • 매우 비효율적이므로 가급적 사용을 피하자

2. 선택 정렬(Selection Sort)

선택 정렬은 배열을 처음부터 순회하여 가장 작은 수를 제일 앞에 둔다. 그리고 맨 앞의 값을 제외한 배열로 다시 반복하는 정렬.

  • 최솟값을 찾아야 하므로 비교 횟수는 많으나, 실제로 교환 횟수가 적음 ( 작은 수, 보통 30 이하에서 효과적이다.)

선택정렬

구현

function selectionSort(arr) {
  let indexMin;
  for (let i = 0; i < arr.length - 1; i++) {
    indexMin = i;
    for (let j = i + 1; j < arr.length; j++) {
      if (arr[j] < arr[indexMin]) {
        indexMin = j;
      }
    }
    [arr[i], arr[indexMin]] = [arr[indexMin], arr[i]];
  }
  return arr;
}

console.log(selectionSort([5,7,1,4,3])) // [ 1, 3, 4, 5, 7 ]

장점

  • 구현이 간단하다.
  • In-place 정렬이다.
  • 작은 수에 효과적

단점

  • 버블 정렬과 마찬가지로 데이터를 하나씩 비교하므로 O(n^2). 비효율적이다.

3. 삽입 정렬(Insertion Sort)

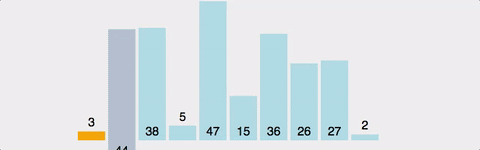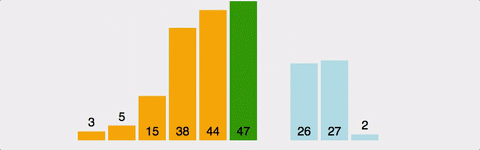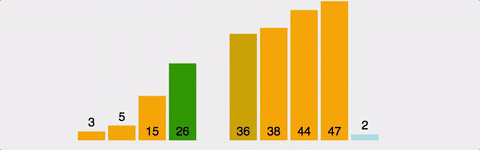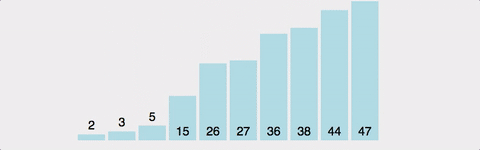
삽입 정렬은 i번째 원소를 정렬된 상태의 앞부분과 비교하여 적절한 위치에 삽입하는 방식.

  • 배열의 마지막 원소까지는 모두 정렬된 상태여야 하며, 마지막부터 첫번째까지의 원소와 i번째 원소를 각각 비교한다.

  • i번째 원소보다 작은 값이 탐색되면 그 위치에 i번째 요소를 삽입한다.

삽입 정렬

구현

function insertionSort(arr) {
  for (let i = 1; i < arr.length; i++) {
    let value = arr[i];
    let prev = i - 1;
    while (prev >= 0 && arr[prev] > value) {
      arr[prev + 1] = arr[prev];
      prev--;
    }
    arr[prev + 1] = value;
  }

  return arr;
}
console.log(insertionSort([5, 6, 1, 2, 4, 3]))

장점

  • 배열이 정렬되어있다면, 가장 좋은 알고리즘
  • In-place 정렬
  • stable 정렬
  • i + 1번째 원소를 배치하는데 필요한 만큼의 원소만 탐색하기 때문에 비교적 효율적이다.
  • 최선의 경우, O(n)의 시간복잡도를 가진다.

단점

  • 평균, 최악의 시간복잡도가 O(n^2)
  • 배열이 길어질수록 비효율적이다.

4. 퀵 정렬 ( Quick Sort )

분할 정복 방법(문제를 작은 2개의 문제로 분리하고 각각을 해결한 다음, 결과를 모아서 원래의 문제를 해결하는 전략)을 통한 정렬로, 하나의 pivot을 정해서 이 pivot보다 작은 값은 왼쪽에 큰값은 오른쪽에 위치시키는 방법.

퀵 정렬

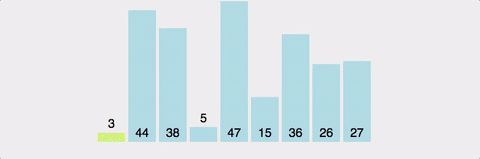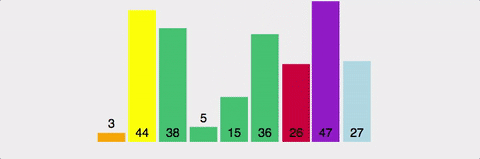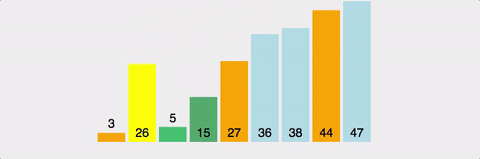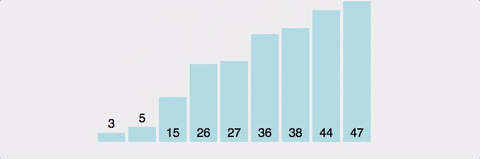
  • 최악의 경우를 제외하고 가장 빠른 정렬이다. 실제로 많이 사용되는 정렬 알고리즘.

  • 퀵 정렬은 다음과 같은 단계로 이루어진다.

    • 분할(Divide)
      • pivot을 기준으로 비균등하게 2개의 부분으로 나눈다. ( pivot 기준 왼쪽이 피벗보다 작은요소, 오른쪽이 피벗보다 큰 요쇼)
    • 정복(Conquer)
      • 부분 배열을 정렬한다. 분할된 배열에 대해 재귀적으로 이 과정을 반복한다.
    • 결합(Combine)
      • 정렬된 부분 배열들을 하나의 배열에 합병한다.
    • 재귀 호출이 진행될 때마다 최소한 하나의 원소는 최종적으로 위치가 정해짐. 그러므로 이 알고리즘은 반드시 끝난다.

구현

function partition(arr, left, right) {
    // 피벗을 기준으로 작은 값은 왼쪽, 큰 값은 오른쪽으로 이동
    const pivot = arr[right];
    let i = left - 1;

    for (let j = left; j < right; j++) {
        if (arr[j] <= pivot) {
            i++;
            // 값 교환
            const temp = arr[i];
            arr[i] = arr[j];
            arr[j] = temp;
        }
    }

    // 피벗 위치 교환
    const temp = arr[i + 1];
    arr[i + 1] = arr[right];
    arr[right] = temp;

    return i + 1;
}

function quickSort(arr, left, right) {
    if (left < right) {
        // 피벗을 기준으로 배열을 분할
        const partitionIndex = partition(arr, left, right);

        // 분할된 부분을 정렬
        quickSort(arr, left, partitionIndex - 1);
        quickSort(arr, partitionIndex + 1, right);
    }
}

console.log(quickSort([4,1,7,6,3,8,2,5])) // [1,2,3,4,5,6,7,8]

장점

  • 한 번 결정된 pivot들이 추후 연산에서 제외되는 특성 때문에, O(nlogn)의 시간복잡도를 가지는 다른 정렬 알고리즘과 비교했을 때 가장 빠르다.
  • In-place 정렬

단점

  • 정렬된 배열에 대해서는 오히려 더 시간이 오래걸린다. (선택 정렬이 더 빠름)
  • Unstable 정렬
  • 최악의 경우 기준(pivot)으로 뽑은 수가 항상 제일 큰 수이거나 제일 작은 수일 경우 O(n^2)의 시간복잡도를 가진다.

5. 합병,머지 정렬(Merge Sort)

분할 정복 알고리즘 중 하나로, 배열을 반으로 나눈 후 각 부분을 재귀적으로 정렬하고, 정렬된 부분을 병합하는 방식.

  • 시간복잡도가 O(n log n)이기 때문에 성능이 준수하여 자주 사용된다.
  • 이미 정렬이된 쪼갠 배열을 차례대로 병합한다.
  • 정렬이 안되어 있다면 재귀를 사용하여 작은 문제로 쪼갠다.

구현

// 두 수 비교
function merge(left, right) {
  let result = [];
  let leftIndex = 0;
  let rightIndex = 0;

  while (leftIndex < left.length && rightIndex < right.length) {
    result.push(
      left[leftIndex] < right[rightIndex]
        ? left[leftIndex++]
        : right[rightIndex++]
    );
  }

  return result.concat(left.slice(leftIndex), right.slice(rightIndex));
}

// 재귀
function mergeSort(arr) {
  if (arr.length <= 1) {
    return arr;
  }

  const middle = Math.floor(arr.length / 2);
  const left = arr.slice(0, middle);
  const right = arr.slice(middle);

  return merge(mergeSort(left), mergeSort(right));
}

console.log(mergeSort([5, 2, 4, 7, 6, 1, 3, 8])) // [1, 2, 3, 4, 5, 6, 7, 8]

장점

  • 최선, 평균, 최악 모두 O(n log n)의 시간복잡도를 가진다.
  • Stable 정렬

단점

  • 추가적인 임시 배열이 필요하다. (추가 메모리 필요)
  • Not In-place 정렬

6. 힙 정렬(Heap Sort)

최대힙 트리나 최소힙 트리를 구성하여 정렬하는 방식

먼저, 힙 (Heap)

힙은 일종의 트리로 수의 집합에서 가장 작은 수(키)나 가장 큰 수만을 자주 꺼내올때 유용한 자료구조

  1. 최대힙 : 완전 트리이면서 Root가 모든 경우에 자식들보다 커야한다.

    • 완전 트리 : 노드가 순서대로 들어있는 트리

  2. 최소힙 : 루트 값이 모든 경우에 자식들보다 작은 값.

힙 정렬

랜덤한 순서의 숫자들을 힙(배열)으로 만들어 넣고, 힙에서 하나씩 제거하면 된다. 가장 큰 값 또는 가장 작은 값 순서로 빠지기 때문에 알아서 정렬된다.

구현

function heapSort(arr) {
    // 최대 힙 구성
    buildMaxHeap(arr);

    // 힙에서 요소 하나씩 추출하면서 정렬
    for (let i = arr.length - 1; i > 0; i--) {
        // 최대값(힙의 루트)을 배열의 끝으로 이동
        swap(arr, 0, i);

        // 힙 크기를 줄여 재구성
        heapify(arr, 0, i);
    }

    return arr;
}

function buildMaxHeap(arr) {
    const len = arr.length;
    // 배열의 중간부터 시작하여 최대 힙 구성
    for (let i = Math.floor(len / 2); i >= 0; i--) {
        heapify(arr, i, len);
    }
}

function heapify(arr, index, heapSize) {
    const left = 2 * index + 1;
    const right = 2 * index + 2;
    let largest = index;

    // 왼쪽 자식이 부모보다 크면 largest를 왼쪽 자식으로 설정
    if (left < heapSize && arr[left] > arr[largest]) {
        largest = left;
    }

    // 오른쪽 자식이 부모 또는 왼쪽 자식보다 크면 largest를 오른쪽 자식으로 설정
    if (right < heapSize && arr[right] > arr[largest]) {
        largest = right;
    }

    // largest가 변경되었을 경우 위치 교환 후 재귀적으로 heapify
    if (largest !== index) {
        swap(arr, index, largest);
        heapify(arr, largest, heapSize);
    }
}

function swap(arr, i, j) {
    const temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

console.log(heapSort([5,3,1,4,7])) // [1,3,4,5,7]

장점

  • 최댓값이나 최솟값을 구할 때 유용하다
  • 멀리 떨어진 요소들을 정렬할 때 유용하다
  • 최선, 평균, 최악 모두 O(nlogn)의 시간복잡도를 가진다 = 성능이 준수하다

단점

  • 같은 시간복잡도를 가지는 다른 알고리즘과 비교하면 느린 편.
  • 사용빈도가 높지 않다.
  • Unstable 정렬

7. 계수 정렬(Counting Sort)

각 항목을 세어 저장해두고, 이를 앞 순서대로 정렬하는 방식. 정수 혹은 정수로 표현할 수 있는 데이터에 대한 정렬 알고리즘

// EX
let arr = [3,1,6,3,4,1,5]

// 각 숫자가 몇 개 나오는지 세어보고
1: 2개, 
3: 2개, 
4: 1개,
5: 1개, 
6: 1개

// 정렬하면
[1,1,3,3,4,5,6]

이처럼 개수를 센 뒤, 1부터 6까지 그대로 갯수대로 나열하는 방식이며, 요소값들을 비교하지 않고 정렬하는 방식이다.

구현시 주의할 점

  • 데이터(값)는 양수여야하고, 값의 범위가 너무 크지않아야 한다.

구현 과정

  • 배열에서 최댓값 찾기
  • 누적 카운트 배열 생성
  • 데이터의 빈도수 카운트
  • 누적 카운트 업데이트
  • 정렬된 결과 배열 생성
  • 누적 카운트 배열을 역순으로 순회하며 각 데이터를 정렬된 위치에 삽입 
function countingSort(arr) {
    const max = Math.max(...arr);
    const count = Array(max + 1).fill(0);

    for (let i = 0; i < arr.length; i++) {
        count[arr[i]]++;
    }
    
    const sortedArray = [];
    for (let num = 0; num < count.length; num++) {
        for (let i = 0; i < count[num]; i++) {
            sortedArray.push(num);
        }
    }

    return sortedArray;
}

console.log(countingSort([4, 2, 2, 8, 3, 3, 1])) // [1, 2, 2, 3, 3, 4, 8]

장점

  • 정렬하는 숫자가 특정 범위 내에 있을 때 유용하다
  • O(n)의 시간복잡도를 가진다.
  • Stable 정렬 (맨 뒤의 수부터 값을 채우기 때문)

단점

  • 메모리 낭비가 심하다 ( 최댓값이 커지면 카운트 배열의 크기가 커지기 때문에 ).
  • Not In-place 정렬

8. 기수 정렬(Radix sort)

각 자릿수를 낮은 자리수에서부터 가장 큰 자리수까지 올라가면서 정렬을 수행하는 방식

  • 기수 정렬은 비교연산을 수행하지 않아 조건이 맞는 상황에서 빠른 정렬 속도를 보장한다.

  • 입력 데이터의 최대값에 따른 계수 정렬의 비효율성을 개선하기 위해 기수 정렬을 사용할 수 있다. 자릿수의 값 별로 정렬을 하므로, 나올 수 있는 값의 최대 사이즈는 9이기 때문

구현 방식

  • 최대 자릿수를 구한다
  • bucket 배열을 하나 만들어, 1의 자리가 같은 원소들을 생성한 배열에 모은다.
  • 10,100...최대 자릿수까지 이를 반복한다.

구현

// 이 코드는 양의 정수 배열에 대해서만 동작한다. 
// 음의 정수나 소수 같은 경우에는 추가적인 처리가 필요하다
function getMax(arr, size) {
  let max = arr[0];
  for (let i = 1; i < size; i++) {
    if (arr[i] > max) {
      max = arr[i];
    }
  }
  return max;
}

function countSort(arr, size, exp) {
  const output = new Array(size).fill(0);
  const count = new Array(10).fill(0);

  for (let i = 0; i < size; i++) {
    count[Math.floor(arr[i] / exp) % 10]++;
  }

  for (let i = 1; i < 10; i++) {
    count[i] += count[i - 1];
  }

  for (let i = size - 1; i >= 0; i--) {
    output[count[Math.floor(arr[i] / exp) % 10] - 1] = arr[i];
    count[Math.floor(arr[i] / exp) % 10]--;
  }

  for (let i = 0; i < size; i++) {
    arr[i] = output[i];
  }
}

function radixSort(arr, size) {
  const max = getMax(arr, size);

  for (let exp = 1; Math.floor(max / exp) > 0; exp *= 10) {
    countSort(arr, size, exp);
  }
}
console.log(radixSort([170, 45, 75, 90, 802, 24, 2, 66]))
// [2, 24, 45, 66, 75, 90, 170, 802]

장점

  • O(n)의 시간복잡도를 가진다
  • 문자열, 정수 정렬이 가능하다. ( 단, 데이터 타입 일정해야함 )
  • Stable 정렬

단점

  • 음수, 양수 따로 구분해서 비교해야 함.
  • Not In-place 정렬
  • 중간 결과를 저장해야 하기때문에, 메모리가 더 필요하다

이미지 출처 및 자료 참고

동쪽별님 티스토리

제로초 정렬

위키피디아

profile
Mintaek
Slow and Steady Wins the Race
이전 포스트

[Data Structure] 자료구조란?

0개의 댓글