K-NN Regression, 선형 회귀(Linear Regression)

Tae Yoon·2024년 6월 28일
머신러닝
0

3-1 K-NN Regression

지도 학습 알고리즘은 크게 분류와 회귀(Regression)으로 나뉜다.
분류: 샘플을 몇 개의 클래스 중 하나로 분류하는 문제
회귀: 임의의 어떤 숫자를 예측하는 문제

데이터준비

import numpy as np
perch_length = np.array([8.4, 13.7, 15.0, 16.2, 17.4, 18.0, 18.7, 19.0, 19.6, 20.0, 21.0,
       21.0, 21.0, 21.3, 22.0, 22.0, 22.0, 22.0, 22.0, 22.5, 22.5, 22.7,
       23.0, 23.5, 24.0, 24.0, 24.6, 25.0, 25.6, 26.5, 27.3, 27.5, 27.5,
       27.5, 28.0, 28.7, 30.0, 32.8, 34.5, 35.0, 36.5, 36.0, 37.0, 37.0,
       39.0, 39.0, 39.0, 40.0, 40.0, 40.0, 40.0, 42.0, 43.0, 43.0, 43.5,
       44.0])
perch_weight = np.array([5.9, 32.0, 40.0, 51.5, 70.0, 100.0, 78.0, 80.0, 85.0, 85.0, 110.0,
       115.0, 125.0, 130.0, 120.0, 120.0, 130.0, 135.0, 110.0, 130.0,
       150.0, 145.0, 150.0, 170.0, 225.0, 145.0, 188.0, 180.0, 197.0,
       218.0, 300.0, 260.0, 265.0, 250.0, 250.0, 300.0, 320.0, 514.0,
       556.0, 840.0, 685.0, 700.0, 700.0, 690.0, 900.0, 650.0, 820.0,
       850.0, 900.0, 1015.0, 820.0, 1100.0, 1000.0, 1100.0, 1000.0,
       1000.0])

훈련 세트, 테스트 세트 분할

from sklearn.model_selection import train_test_split
train_input, test_input, train_target, test_target=train_test_split(perch_length, perch_weight, random_state=42)

reshape() 메서드를 이용해 train_input과 test_input을 2차원 배열로 바꾼다. 기존 train_input의 크기는 (42.)이다. 이를 2차원 배열 (42, 1)로 바꾸기 위해 기존에 알고 있는 방식은 reshape(42, 1)으로 하면 되지만 넘파이는 배열의 크기를 자동으로 지정하는 기능을 제공한다. 크기에 -1을 지정하면 나머지 원소 개수로 모두 채우라는 뜻. 
train_input=train_input.reshape(-1, 1)
test_input=test_input.reshape(-1, 1)

결정계수(R2R^2)

K-NN 회귀 알고리즘을 구현한 클래서는 KNeighborsRegressor

from sklearn.neighbors import KNeighborsRegressor
knr=KNeighborsRegressor()
knr.fit(train_input, train_target)
print(knr.score(test_input, test_target))

0.992809406101064으로 높은 점수

분류의 경우 테스트 세트에 있는 샘플을 정확하게 분류한 개수의 비율을 점수로 반환
회귀의 경우 결정계수를 점수로 반환한다
R2=1−(타깃−예측)2의합(타깃−평균)2의합R^2=1-\frac{(타깃-예측)^2의 합}{(타깃-평균)^2의합}
타깃의 평균 정도를 예측하는 수준이면 0에 가까워 지고, 예측이 타깃에 가까워지면 1에 가까운 값

과대적합, 과소적합

print(knr.score(test_input, test_target))
print(knr.score(train_input, train_target))

테스트 점수는 0.99, 훈련 점수는 0.96으로 테스트 점수가 더 높다.
모델을 훈련 세트에 훈련하면 훈련 세트에 잘 맞는 모델이 만들어진다.
일반적으로 훈련 세트의 점수가 더 높게 나온다.

과대적합: 훈련 세트에서는 점수가 굉장히 좋았는데 테스트 점수에서 점수가 나쁘게 나왔다.

과소적합: 훈련 세트보다 테스트 세트의 점수가 높거나 두 점수가 모두 너무 낮은 경우(모델이 너무 단순하여 훈련 세트에 적절히 훈련되지 않은 경우)

지금의 경우는 과소적합으로 모델을 더 복잡하게 만들어야한다.
K-NN의 모델을 복잡하게 만드는 방법을 이웃의 개수 K를 줄이는 것.
이웃의 개수를 줄이면 훈련 세트에 있는 국지적인 패턴에 민감.
이웃의 개수를 늘리면 데이터 전반에 있는 일반적인 패턴을 따를 것이다.

이웃의 개수를 줄여 다시 학습

knr.n_neighbors=3
knr.fit(train_input, train_target)
print(knr.score(train_input, train_target))
print(knr.score(test_input, test_target))

0.9804899950518966
0.9746459963987609
테스틑 세트의 점수가 훈련 세트의 점수보다 낮아졌으므로 과소적합 문제 해결

3-2 선형 회귀(Linear Regression)

데이터는 위에서 사용한 그대로 사용
길이가 50cm인 무게 예측

print(knr.predict([[50]]))

1,033g 정도로 예측 그러나 실제로는 더 많이 나간다고 한다.

distances, indexes=knr.kneighbors([[50]])
plt.scatter(train_input, train_target)
plt.scatter(train_input[indexes], train_target[indexes], marker='D')
plt.scatter(50, 1033, marker='^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()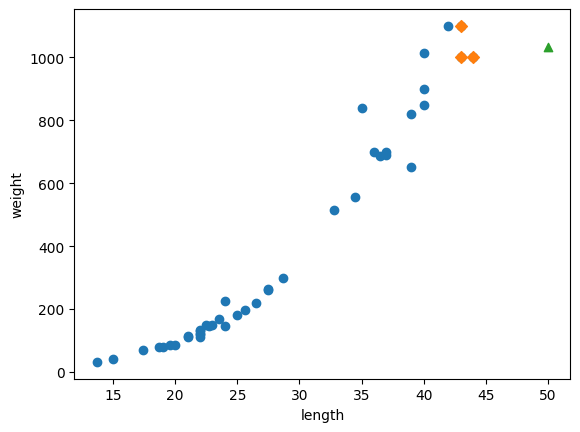

이웃 샘플의 타깃의 평균을 구한다

print(np.mean(train_target[indexes]))

1,033g으로 모델의 예측값과 일치

100cm의 경우에 시각화를 하였다

distances, indexes=knr.kneighbors([[100]])
plt.scatter(train_input, train_target)
plt.scatter(train_input[indexes], train_target[indexes], marker='D')
plt.scatter(100, 1033, marker='^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()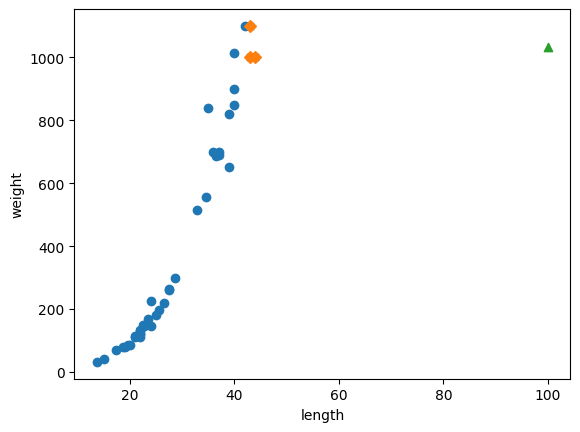


100cm의 경우에도 1,033g으로 50cm의 경우와 같다.
이런 이유는 K-NN 회귀는 가장 가까운 샘플을 찾아 평균하기 때문에 새로운 샘플이 훈련 세트의 범위를 벗어나면 엉뚱한 값을 예측할 수 있다.
이를 해결하기 위해 선형 회귀를 사용할 수 있다.

선형 회귀

특성이 하나인 경우 어떤 직선을 학습하는 알고리즘
sklearn.linear_model 패키지 아래 LinearRegression 클래스로 선형 회귀 알고리즘을 구현

from sklearn.linear_model import LinearRegression
lr=LinearRegression()
lr.fit(train_input, train_target)
lr.predict([[50]])

결과는 1241.8g 으로 K-NN 회귀를 사용했을 때보다 무게를 높게 예측했다.
직선 방정식 y=ay=a x x+bx +b
x를 농어의 길이, y를 농어의 무게로 바꾸면 된다.
LinearRegression 클래스가 찾은 기울기(a), 절편(b)는 coef, intercept 속성에 저장되있다

print(lr.coef_, lr.intercept_)
[39.01714496] -709.0186449535477

결정 계수를 구한다

print(lr.score(train_input, train_target))
print(lr.score(test_input, test_target))
0.939846333997604
0.8247503123313558

다항 회귀

선형 회귀에서 만든 직선은 y축이 0보다 내려 가는 경우가 있었다. 이건 현실에서 일어날 수 없는 일이다.
관점을 바꿔서 최적의 직선보다 최적의 곡선을 찾는다라 생각해보자.
2차 그래프를 그리려면 훈련 세트에 길이를 제곱한 값이 추가 되야한다.

train_poly=np.column_stack((train_input**2, train_input))
test_poly=np.column_stack((test_input**2, test_input))

원래 특성이 길이를 제곱헤 왼쪽에 추가 했기 때문에 훈련, 테스트 모두 2개의 열로 늘어났다.
이를 다시 선형 회귀 모델로 훈련하여 예측해보자.

lr.fit(train_poly, train_target)
lr.predict([[50**2, 50]])
array([1573.98423528])
print(lr.coef_, lr.intercept_)
[  1.01433211 -21.55792498] 116.0502107827827

훈련, 테스트 세트의 점수도 크게 높아졌다.

print(lr.score(train_input, train_target))
print(lr.score(test_input, test_target))
0.939846333997604
0.8247503123313558

3-3

다중 회귀(multiple regression)

여러 개의 특성을 사용한 선형 회귀

데이터 준비

import pandas as pd
df=pd.read_csv('https://bit.ly/perch_csv_data')
perch_full=df.to_numpy()
train_input, test_input, train_target, test_target=train_test_split(perch_full, perch_weight, random_state=42)

변환기

사이킷런에서 특성을 만들거난 전처리하기 위한 다양한 클래스
include_bias=False으로 지정하여 절편을 위한 항을 제외하고 반환

from sklearn.preprocessing import PolynomialFeatures
poly=PolynomialFeatures(include_bias=False)
poly.fit([[2,3]])
poly.transform([[2,3]])
array([[2., 3., 4., 6., 9.]])

get_feature_names_out() 메서드를 이용하여 특성이 각각 어떤 입력의 조합으로 만들어 졌는지 알려준다

poly.get_feature_names_out()
['x0', 'x1', 'x2', 'x0^2', 'x0 x1', 'x0 x2', 'x1^2', 'x1 x2', 'x2^2']

변환된 특성을 사용해 다중 회귀 모델을 훈련

test_poly=poly.transform(test_input)

다중 회귀 모델 훈련

lr.fit(train_poly, train_target)
print(lr.score(train_poly, train_target))
print(lr.score(test_poly, test_target))
0.9903183436982125
0.9714559911594111

특성을 많이 추가한다면 훈련 세트에 대해서는 거의 완벽하게 학습되지만
훈련세트에 과대적합하여 테스트 세트에서는 낮은 점수를 만든다

규제

머신러닝 모델이 훈련 세트를 너무 과도하게 학습하지 못하도록 만든다
변환기 중 하나인 StandardScaler 클래스를 사용

from sklearn.preprocessing import StandardScaler
ss=StandardScaler()
ss.fit(train_poly)
train_scaled=ss.transform(train_poly)
test_scaled=ss.transform(test_poly)

선형 회귀 모델에 규제를 추가한 모델을 릿지(Ridge), 라쏘(Lasso)라고 한다.

릿지(Ridge) 회귀

from sklearn.linear_model import Ridge
ridge=Ridge()
ridge.fit(train_scaled, train_target)
print(ridge.score(train_scaled, train_target))
print(ridge.score(test_scaled, test_target))
0.9896101671037343
0.9790693977615387

과대적합하지 않아 테스트에서도 좋은 결과를 보인다
릿지와 라쏘는 규제의 양을 임의로 매개변수 alpha를 통해 조절할 수 있다.

train_score=[]
test_score=[]
alpha_list=[0.001, 0.01, 0.1, 1, 10, 100]

for alpha in alpha_list:
  ridge= Ridge(alpha=alpha)
  ridge.fit(train_scaled, train_target)
  train_score.append(ridge.score(train_scaled, train_target))
  test_score.append(ridge.score(test_scaled, test_target))

plt.plot(np.log10(alpha_list), train_score)
plt.plot(np.log10(alpha_list), test_score)
plt.xlabel('alpha')
plt.ylabel('R^2')
plt.title('Lidge')
plt.show()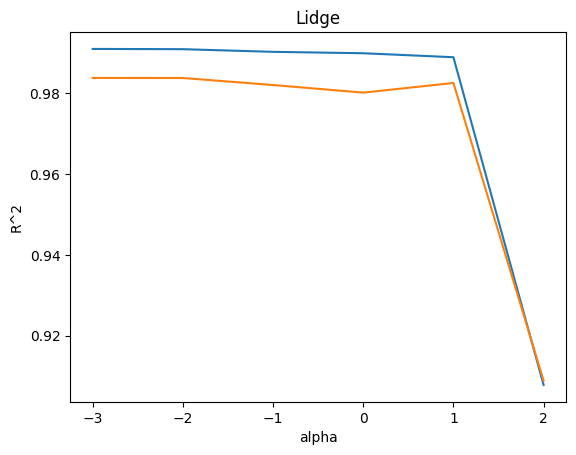


그래프에서 위에가 훈련 세트, 아래가 테스트 세트이다.
그래프를 통해 적절한 alpha값은 0.1이라는 결과를 보인다.

라쏘(Lasso) 회귀

from sklearn.linear_model import Lasso
lasso=Lasso()
lasso.fit(train_scaled, train_target)
print(lasso.score(train_scaled, train_target))
print(lasso.score(test_scaled, test_target))
0.989789897208096
0.9800593698421883

라쏘 또한 과대적합을 잘 억제한 결과를 보인다

train_score=[]
test_score=[]
alpha_list=[0.001, 0.01, 0.1, 1, 10, 100]

for alpha in alpha_list:
  lasso= Lasso(alpha=alpha)
  lasso.fit(train_scaled, train_target)
  train_score.append(lasso.score(train_scaled, train_target))
  test_score.append(lasso.score(test_scaled, test_target))
  
plt.plot(np.log10(alpha_list), train_score)
plt.plot(np.log10(alpha_list), test_score)
plt.xlabel('alpha')
plt.ylabel('R^2')
plt.title('Lasso')
plt.show()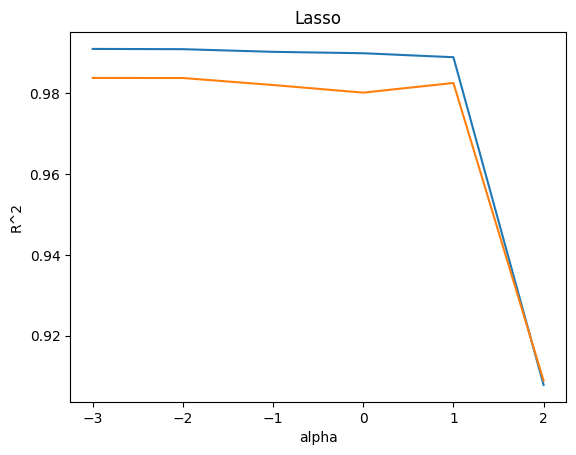


그래프에서 왼쪽은 과대적합을 보여주고, 오른쪽으로 갈수록 훈련, 테스트 간의 점수가 좁혀지고 있다.
가장 오른쪽의 점수가 크게 떨어지는 부분은 과소적합이 되는 것을 볼 수 있다.
라쏘에서 최적의 alpha는 10이라는 결과를 보인다.

profile
Tae Yoon
이전 포스트

K-최근접 이웃(K-NN)

다음 포스트

로지스틱 회귀

0개의 댓글

관련 채용 정보