float vs long
float 의 바이트가 더 적은데 어떻게 long보다 넓은 범위를 표현할까?
실수 와 부동 소수점
실수 표현과 부동 소수점에 대해 이해하기 위해서는 먼저 '실수'와 '부동 소수점'이 무엇인지 알아야 합니다.
실수(Real Number):
실수는 소수점이 있는 숫자를 말합니다. 예를 들어, 3.14, 0.01, -2.5 등이 실수입니다.
이러한 실수는 컴퓨터에서 표현하기 위해 '부동 소수점' 방식을 사용합니다.
부동 소수점(Floating Point):
부동 소수점은 실수를 컴퓨터에서 표현하는 방식입니다. '부동'이란 단어가 의미하는 것은
소수점의 위치가 고정되어 있지 않고, '움직일 수 있다'는 것입니다.
이 방식은 매우 큰 수나 매우 작은 수를 표현하는 데 유용합니다.
예를 들어, 0.000123과 123000000.0 두 수를 생각해봅시다.
이 두 수를 부동 소수점으로 표현하면, 각각 1.23 x 10^-4와 1.23 x 10^8로 표현할 수 있습니다. 여기서 1.23은 '가수(mantissa)'라고 하고, -4와 8은 '지수(exponent)'라고 합니다.
이처럼 부동 소수점은 가수와 지수로 이루어져 있습니다.
결론
정수타입(long)은 지수를 사용하지 못하고, 실수타입(float)은 지수를 사용할 수 있다. => 제곱의 사용으로 훨씬 더 큰 수(범위)를 만들어 낼 수 있다.
long의 범위 : long은 64비트(8바이트)를 사용하여 정수를 표현합니다. 이는 2의 64승, 즉 약 -9,223,372,036,854,775,808부터 9,223,372,036,854,775,807까지의 정수를 표현할 수 있습니다.
약 -922경 3372조 368억 5477만 5807 ~ +922경 3372조 368억 5477만 5807
float의 범위 : 반면에 float는 32비트(4바이트)를 사용하여 실수를 표현합니다. 그러나 이 32비트는 부동 소수점 방식에 따라 '가수'와 '지수'로 나뉘어 사용됩니다. 이 방식 덕분에 float는 매우 큰 수(약 10^38)부터 매우 작은 수(약 10^-38)까지 표현할 수 있습니다.
약 +-100,000,000,000,000,000,000,000,000,000,000,000,000 > 백간(^38)
억(^8) < 조(^12) < 경(^16) < 해(^20) < 자(^24) < 자(^24) < 양(^28) < 구(^32) < 간(^36) <백간(^38)
public class Main {
public static void main(String[] args) {
long a = 10000000000L; // 10^10, long으로 표현 가능
float b = 10000000000F; // 10^10, float으로 표현 가능
long c = 10000000000000000000L; // 10^19, long으로 표현 불가능
float d = 10000000000000000000F; // 10^19, float으로 표현 가능
long e = 0.1L; // 0.1, long으로 표현 불가능
float f = 0.1F; // 0.1, float으로 표현 가능
}
}10진수의 2진수 변환
10진수 -> 2진수 변환방법
1) 정수부분
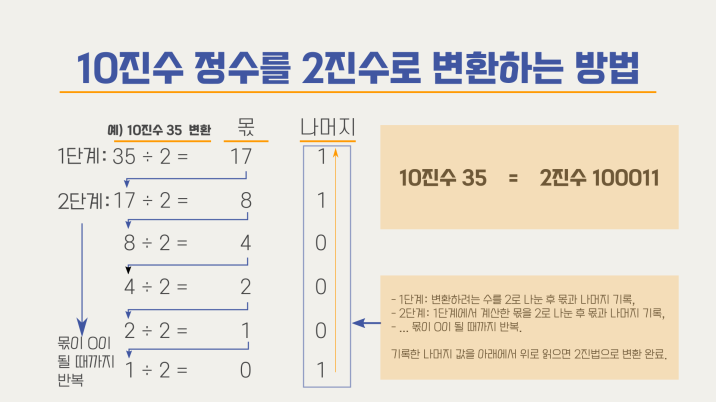
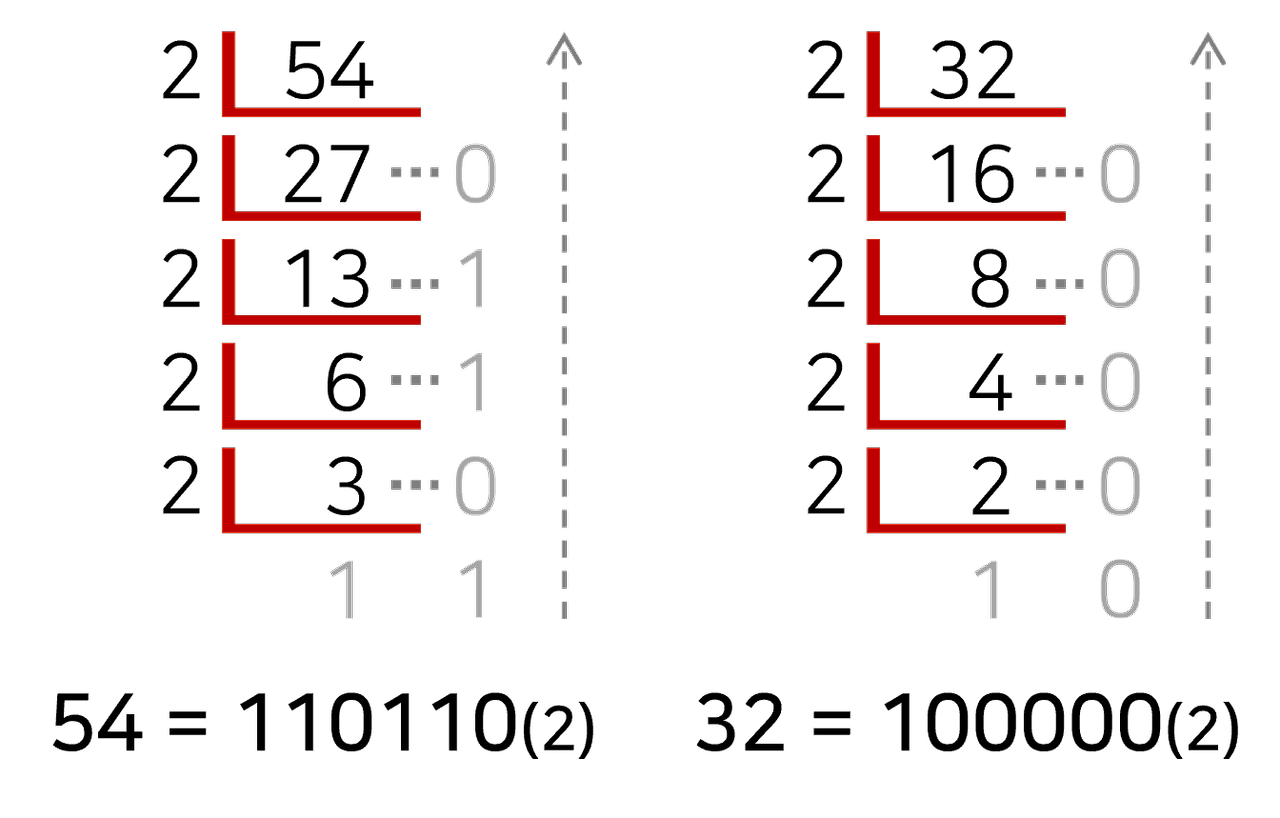
10진수를 2진법으로 변환하는 방법은 10진수 숫자를 2로 나눌 수 없을 때까지 나누고 아래에서부터 꺼꾸로 나열하면 변환할 수 있다.
* 큰 숫자 를 변환할 때

2) 소수부분
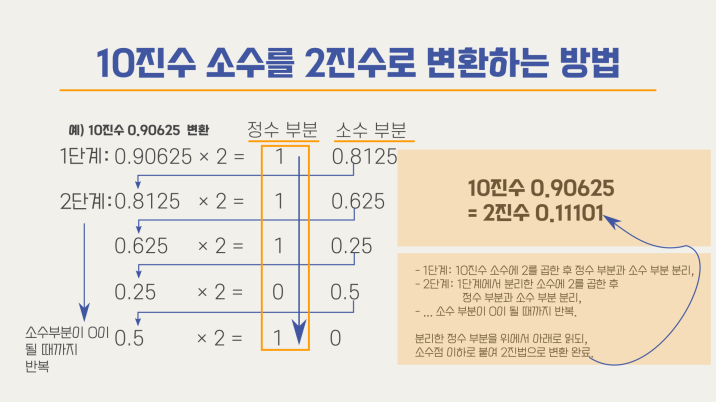
소수 부분을 2로 계속 곱해서 정수 부분이 1이 되면 2진수에서 1로 변환, 정수 부분이 0이 되면 2진수에서 0으로 변환하고 소수부분이 0이 될 때까지 나머지 소수 부분에 계속 2를 곱한다.
무한이 나누어 질때
소수 부분이 0으로 나누어 떨어지지 않고 무한히 나누어지는 경우가 있다. 이때는 무한 소수로 나타낸다.
2진수 -> 10진수 변환방법
1) 정수부분
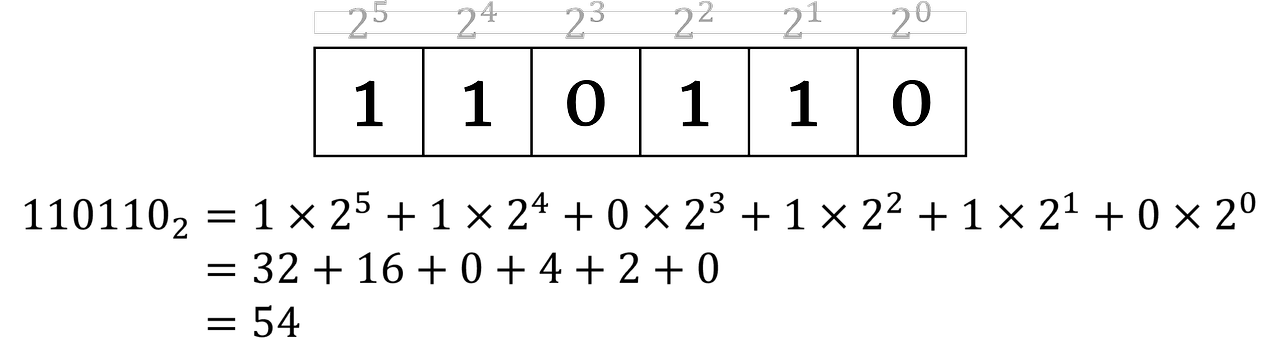
2) 소수부분 + (정수 부분)
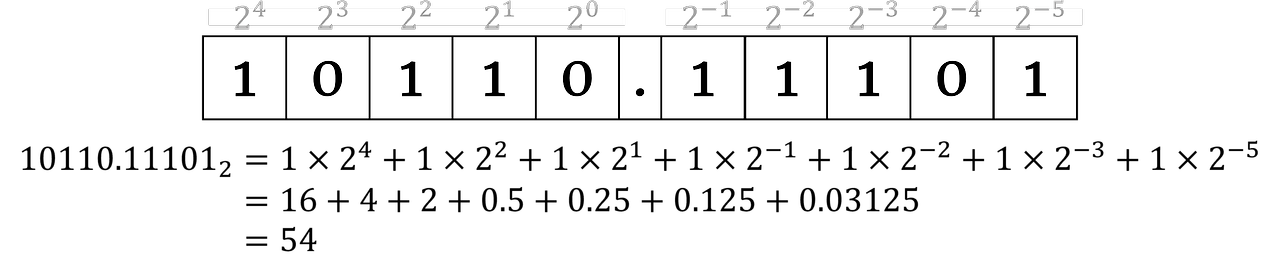
출처 : https://blog.hexabrain.net/357
출처 : https://ourcalc.com/2%EC%A7%84%EC%88%98-%EB%B3%80%ED%99%98%EA%B8%B0/
