반갑다. 아쎄이들. 오늘은 바다 속에서 소리가 어떻게 전파가 되는지 알아볼거야.

Propagation Loss

Propagation Loss(PL), 일명 전파 감소는 음원과 이로부터 멀리 떨어진 receiver 사이에서의 소리 강도의 감소를 정량적으로 측정한 값이다. Io가 소리가 발생한 지점에서 1미터 떨어진 곳의 음 강도이고 Ir은 receiver에서의 음 강도라면 PL을 아래와 같은 식으로 표현할 수 있다.

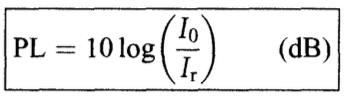
Losses

PL을 정량화하는 방식으로 확산 과정에서 발생한 손실과 흡수하는 과정에서 발생한 손실의 합으로 계산하는 방식이 있다. 또 다른 방법으로는 산란과 굴절을 이용하여 계산하는 방법이 있는데 이것은 나중에 다루겠다.

Spreading Losses

The spherical spreading law

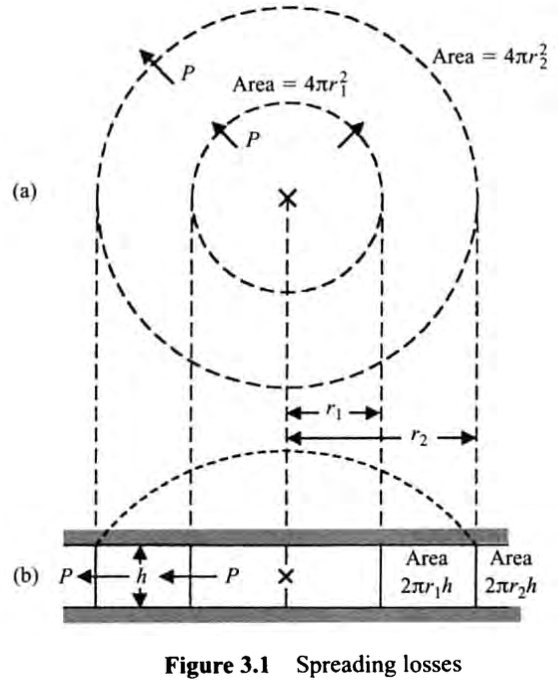
아래의 그림 3.1의 a 부분을 봐라. 음원이 무한하고 무손실의 매질에 위치한 경우에 힘은 모든 방향으로 동일하게 전파된다. 소리는 음원을 기준으로 구형태를 그리면서 퍼져나간다. 이때 소리가 아무리 넓게 퍼져도 음원에서 기원한 Power는 변하지 않는다. 그러므로 Power = Intensity X area 이다.

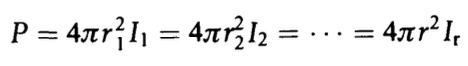
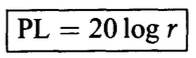
The cylindrical spreading law

이번에는 그림 3.1의 b를 봐라. 음원이 h 미터로 떨어져있는 평행한 평면으로 둘러쌓여있는 경우 음원을 둘러싼 증가하는 원통형 표현을 가로지르는 힘은 다음과 같이 표현할 수 있다.

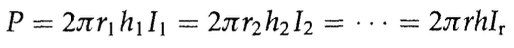
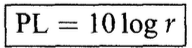
Absorption Losses

음파가 바닷물을 통과할 때 두 가지 주요 메커니즘을 통해 흡수 손실이 발생한다.

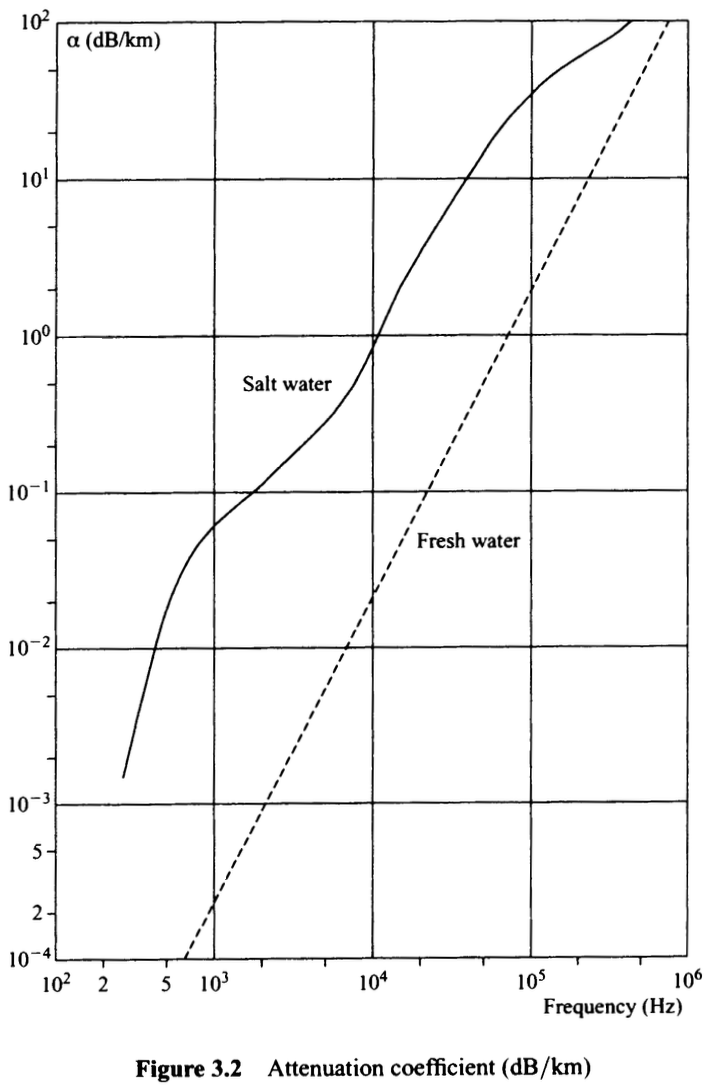
Viscosity(점도): 점도로 인한 손실은 담수와 바닷물 모두에 존재한다. 점도는 주파수의 제곱에 비례한다. 이러한 주파수 의존성은 아래 그림 3.2의 로그-로그 그래프에서 직선으로 나타난다. 로그-로그 그래프는 변수들의 지수적 관계를 선형 관계로 변환하여, 주파수와 점성에 의한 손실 사이의 관계를 더 명확하게 볼 수 있게 한다. 해당 그래프에서 담수는 가파른 직선을 그리고 있다. 이것을 통해 주파수와 점도의 상관관계를 알 수 있다. 해수에 대해서는 조금 다른 형태를 그리고 있는데 이것은 해수는 여러가지 다른 요인들이 많아 그 관계가 복잡하여 조금 형태가 다른 것이다.

Molecular relaxation: Molecular relaxation에 대한 손실은 해수에서만 나타난다. 이것은 소리 파동이 유체를 통과할 때 일어나는 압력 변화에 의해 유체 내의 분자들이 이온으로 변환되는 현상을 말한다. 이 과정에서 에너지 흡수가 발생하게 되는데 그 결과로 인해 소리의 강도가 감소하게 된다. 해수에서는 황산마그네슘(2 to 500 kHz)과 붕산(Below 2 kHz)이 이 역할을 담당한다.

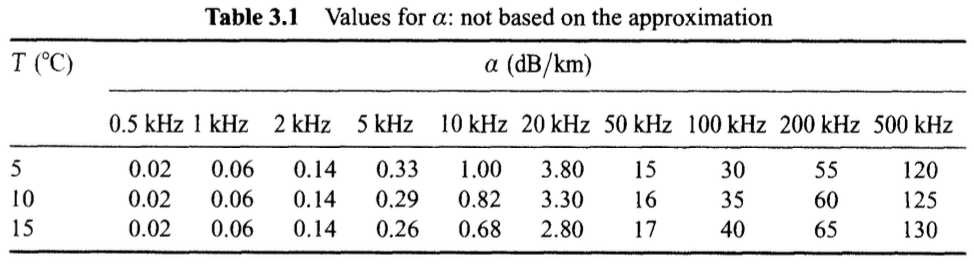
이러한 손실에 대한 광범위한 측정이 이루어졌으며 주파수, 수심(압력) 및 염분과 관련된 몇 가지 경험식이 존재한다. 총 손실은 감쇠 계수인 a(dB/km)로 표시된다.
감쇠 계수 a는 주파수에 따라 급격히 증가하고 온도에 따라 변화한다. 또한 수심과 염도에 따라 달라지지만 그 강도는 덜하다. 그림 3.2는 프랑소와와 해리슨의 공식에 따라 온도 10°C와 염도 35ppt에서 주파수에 따른 a의 변화를 나타낸 것이다.

0.5kHz와 100HZi 사이의 '표준' 해수에 대한 근사치는 다음과 같다.

아래 표는 수온과 주파수에 따른 감쇄를 나타낸 것이다.

Spherical Spreading and Absorption

구형 확산과 흡수 손실의 합을 통해 초기 설계와 포퍼먼스 비교를 합니다.

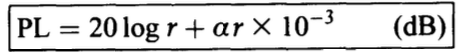
Propagation losses 와 복잡한 propagation model을 측정했을 때 매우 정확한 결과가 자주 나타납니다. 하지만 짧은 거리를 제외하고는 구형 확상을 방해하는 요소가 존재하기 때문에 일반적으로 비관적으로 바라 봅니다. 그래서 일부 사람들은 15 log r을 타협안으로 사용하기도 합니다.

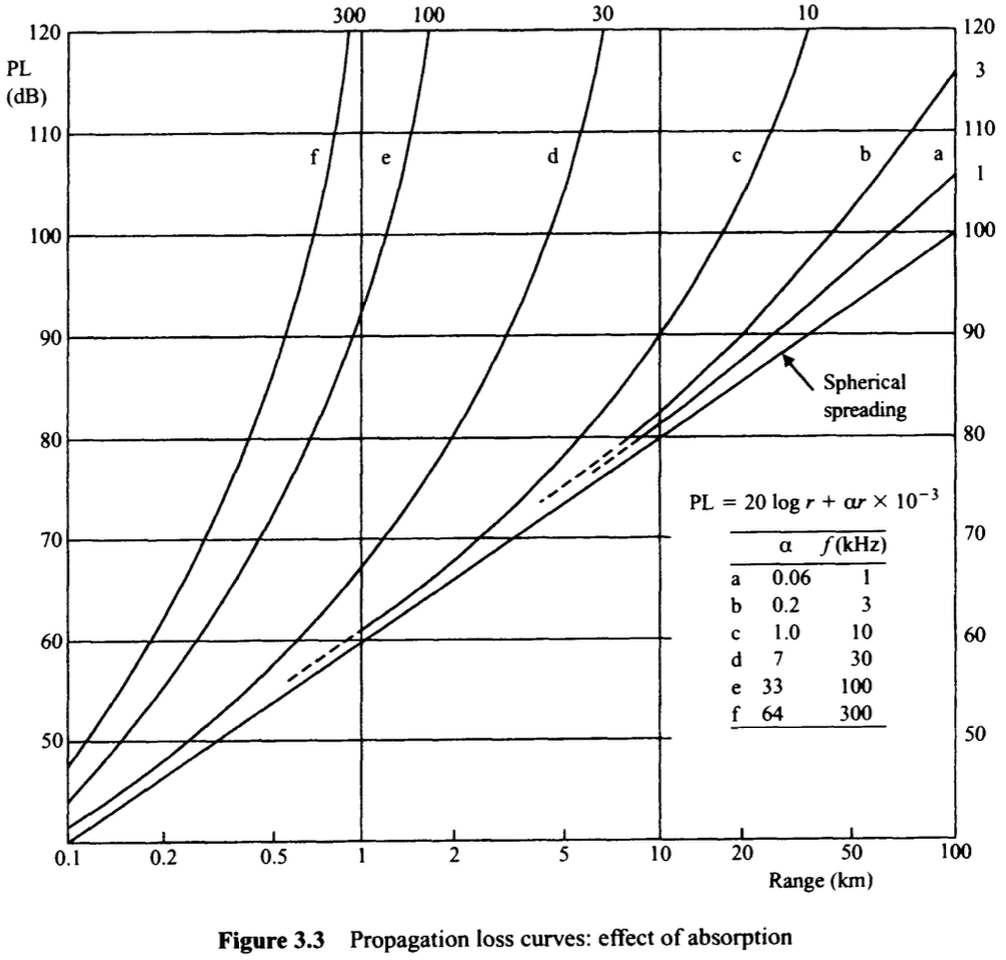
그림 3.3은 구형 확산 손실을 단독으로 또는 선택한 주파수에서 흡수를 추가하여 나타낸 것이다. 100km에서도 1KHz 이하에서는 흡수가 미미한 반면, 100kHz에서는 2km에서도 흡수가 엄청나다는 것을 알 수 있다.

Propagation in the Real Ocean

반사, 산란, 표층과 해저라는 해양 경계의 존재로 인해 아주 짧은 거리를 제외하고는 실제 바다에는 자유로운 조건이 존재하지 않으며, 이를 고려한 신뢰할 수 있는 모델을 개발하는 데 여전히 많은 노력을 기울이고 있다.
바다의 음속, 즉 절대값과 더 중요한 것은 수심에 따른 변화는 모든 모델에서의 기본이다. 음속 프로파일(SSP)에 대한 지식은 소나 설계자와 운영자가 그림자 영역을 피하기 위해 견인 어레이 또는 가변 수심 소나(VDS)를 적절한 수심에 배치하거나 선체 장착 소나의 빔을 눌려서 바닥 바운스 또는 수렴 영역(CZ) 경로를 활용하는 등 적절한 소나 전파 모드를 선택하는 데 도움이 될 수 있다.

The Speed of Sound

바다의 음속은 온도, 압력(수심), 염도에 따라 달라진다. 음속을 계산하는 데는 다양한 경험적 공식이 존재하는데, 이것 중 하나가 Leroy의 공식이 이다.

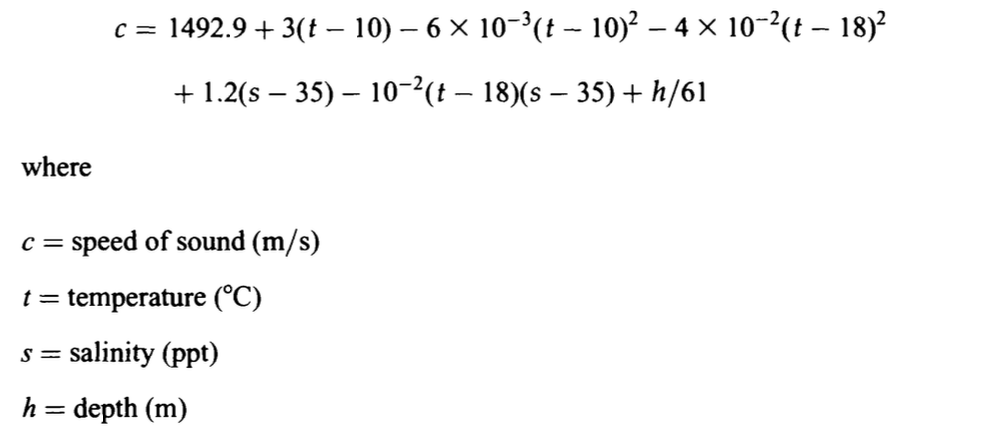
1O"C, 수심 0, 염도 35 ppt에서 음속은 149Om/s이다. 다음은 이 '표준' 음속과 함께 사용할 수 있는 대략적인 음속 계수이다:

Sound Speed Profiles

Sound speed profiles (SSPs)는 깊이에 따른 바다의 소리 속도를 그래프화한 것이다. SSP는 장소, 계절, 날짜, 날씨에 따라 다르다. 대부분의 장소에 염도는 35ppt 라는 상수로 간주한다. 그러나 몇몇 환경에서는 다른 염도를 가지고 있다. 강 하구 근처에는 염도는 매우 다양하다. 그리고 북극의 얼음이 녹는다는 것은 표면 근처의 염도가 낮아진다는 것을 의미하며, 발트해의 일부 지역에서는 모든 수심에서 매우 낮은 염도가 존재한다.
또한 염도가 낮으면 감쇠 계수가 매우 낮아 전파 손실이 줄어든다. 발트해에서만 작동하도록 설계된 소나는 크기와 비용을 줄이면서 일반 염도에 필요한 것보다 더 높은 주파수를 사용할 수 있다.
가장 가변적이고 측정하기 가장 어려운 것은 수심에 따른 바다의 온도이다. 일반적으로 선박이나 항공기에서 배치할 수 있는 수온계로 측정하며, 일반적으로 정확도 또는 분해능은 약 0.25°C다.

음속은 온도와 깊이에 따라 증가한다. 수면 근처의 물이 더 깊은 곳보다 따뜻할 때는 수심이 깊어질수록 두 가지 상반된 경향이 나타난다.

• 온도가 낮아지면 음속이 감소.
• 압력이 높아지면 음속이 증가.

이러한 상반된 경향의 결과로 수심 수백 미터 내에서 매우 다양한 SSP가 생성되며, 이러한 SSP는 일교차 변화와 바람과 파도에 의한 표층의 혼합으로 인해 더욱 복잡해진다.

그림 3.4는 4가지 층에 따른 SSP가 갈라지는 전형적인 모습을 보여주고 있다.

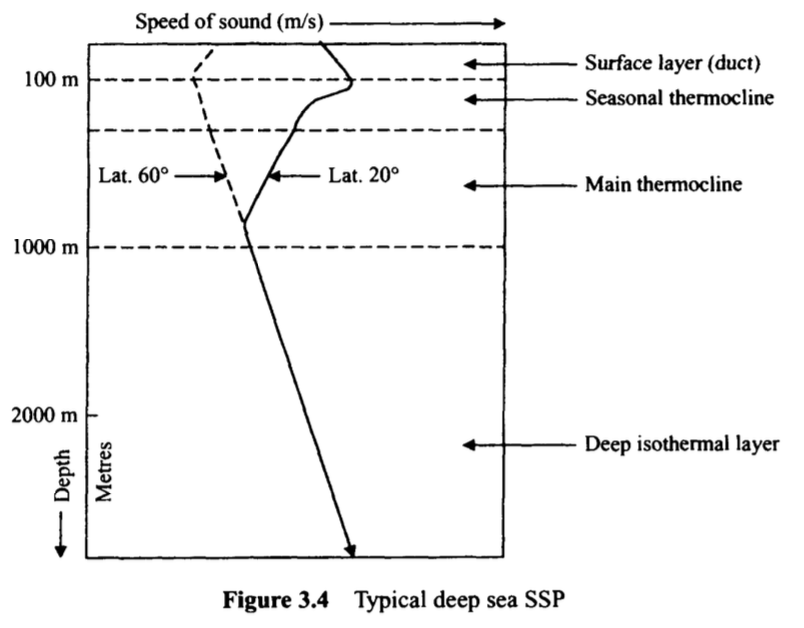
• Surface layer(표층): 바다 표면에서 바람의 작용에 의해 혼합된 등온수 층이다. 소리는 표면 반사와 상향 굴절에 의해 이 층에 갇히는 경향이 있다.
• Seasonal thermocline: 수심이 깊어질수록 온도가 낮아진다. 여름과 가을에는 이 층이 강해져 식별이 가능하다. 겨울과 봄에는 약해져 표층과 합쳐진다.
• Main thermocline: 계절의 영향을 거의 받지 않는다. 수심에 따라 압력이 증가하지만, 온도와 압력 변화에 효과가 얽혀 결국에는 소리의 속도가 낮아지는 곳이다.
• Deep isothermal layer: 바닥까지 약 4°C의 일정한 온도를 유지한다. 음속은 압력이 증가함에 따라 증가한다. 고위도에서는 이 층이 해수면에 더 가깝게 확장되며, 북극에서는 다른 층은 아예 없어질 수도 있다. 이러한 경향은 위도가 약 60도인 경우 그림 3.4의 점선 곡선으로 표시되어 있다.

Deep Sound Channel

Main thermocline의 감소 경사와 Deep isothermal layer의 증가 경사 사이에, sound speed minimum이 존재한다. 이 지점에서 소리가 굴절되어 소리가 집중되는 현상이 있다. 이러한 굴절 현상은 소리 파동이 해당 최소 속도 지점을 따라 전파되도록 하여 에너지 손실 없이 멀리까지 전달되게 합니다. 이 최소 속도 지점에서 발생하는 집중 현상으로 인해 형성되는 음향 도관을 깊은 소리 채널(Deep Sound Channel, DSC)이라고 한다.
이 현상을 이용하기 위해서 DSC에 위치하여 소음을 발생시키면 이 효과를 가장 크게 경험할 수 있다.
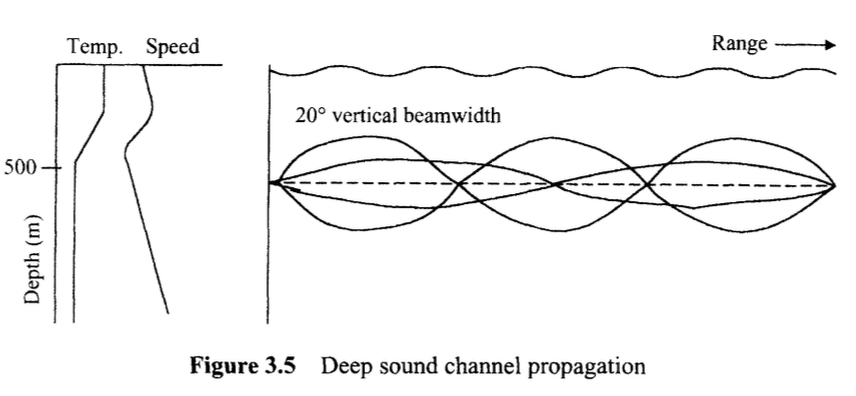
그림 3.5는 DSC에서 소음을 발생시켰을 때의 Sound Ray를 나타내고 있다. 이때 수직적인 beamwidth가 대략 20도가 나오는 것을 알 수 있다.

Reliable Acoustic Path

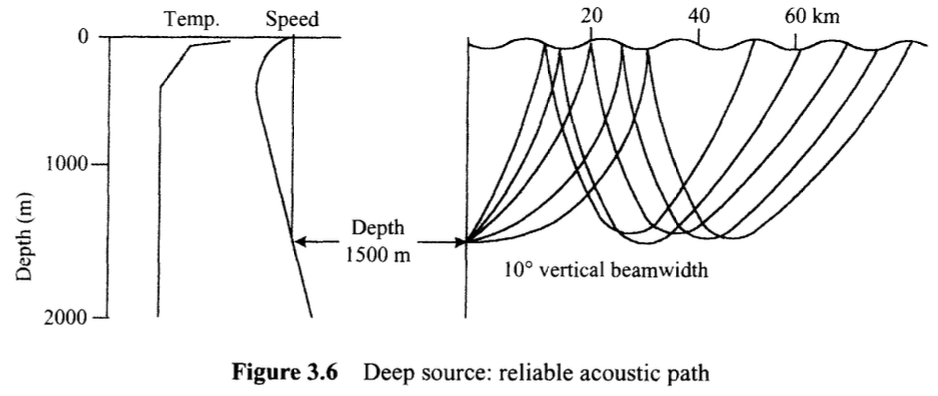
음향신호의 원천을 깊은 바다(적어도 1000m) 속에 위치함으로써 일반적으로 잠수함이 잠수하는 위치의 타켓을 탐지할 수 있다.(그림 3.6) 이렇게 소리를 얻는 방식은 가변적인 수면과 해저의 의한 손실에 덜 민감하기에 신뢰할 만 하다고 한다. 이 Reliable Acoustic Path, 일명 RAP의 조건은 음향신호의 원천이 표면과 음향 속도가 같은 정도 수준까지 내려가야 한다.(그림 3.7)

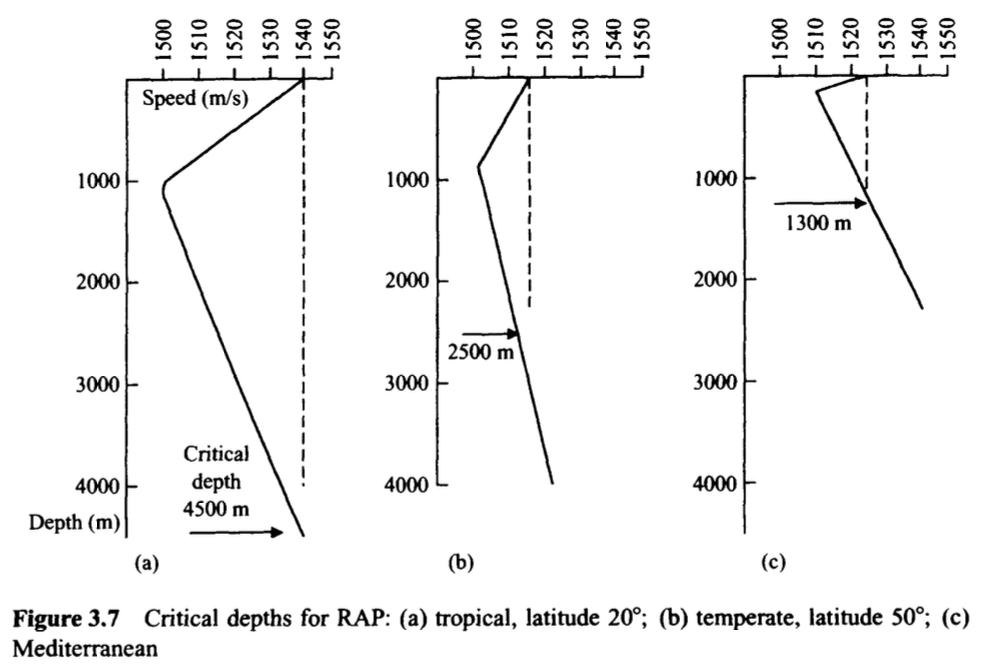
특히, 고위도에서, DSC는 RAP의 임계 깊이와 가까워질 수 있다. 그리고 수직으로 5도 정도 소나빔을 조정할 수 있거나 다양한 깊이에 소나를 배치할 수 있는 기능이 있다면 shadow zones(음향이 해양의 지면이나 수면 등의 다양한 영향에 의해 도달하지 못하는 지역)을 지우는데 도움이 될 것이다.

아주 깊은 수심 (DSC의 경우 500m, RAP의 경우 1000m)에서 소음원과 receiver를 같이 설치하는 것은 심각하게 공학적으로 구동적으로 제한이 있다. 예를 들자면 1000m의 수심에서 작동하는 소자를 만들어내는 것은 어렵지만 가능하나 source level에 한계가 있다.

Surface Duct Propagation

표층 바람과 파도가 바다의 얕은 층을 섞어 거의 등온층을 만들면 압력 효과가 지배적으로 작용하여 수온이 떨어지기 시작하는 깊이, 즉 층의 바닥으로 내려가면서 음속이 증가하여 최소 DSC에 도달할 때까지 음속이 감소하기 시작한다. 이 등온층인 수압 덕트는 최소 5m에서 최대 200m까지 존재할 수 있으며, 일반적으로 50~100m의 덕트는 전 세계 추운 바다에서 흔히 볼 수 있다.

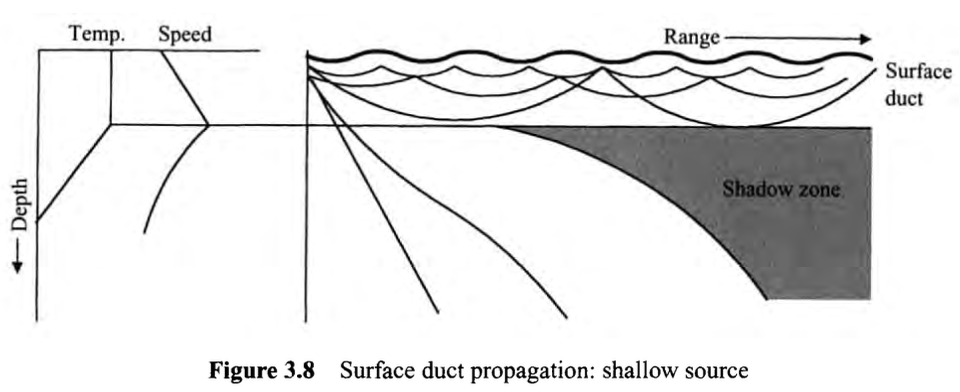
그림 3.8을 보면 수평에 가깝게 투사된 광선은 위쪽으로 굴절되어 여러 번의 표면 반사를 거친다. 반면, 층을 투과하는 광선은 처음에 아래쪽으로 굴절되어 Shadow zone 이라고 하는 영역이 생성되는데, 이 영역에서는 소리 에너지가 거의 투과하지 않는다. 따라서 Shadow Zone 내, 즉 레이어 아래에 있는 표적은 탐지하기 어렵다. 바다의 모든 전파가 그렇듯이, 단순한 ray trace가 가능한 방법은 존재하지 않다. Shadow zone은 음의 강도가 크게 감소하고 표면에서의 음의 방향 전환이 크게 발생하지 않는 영역이다.

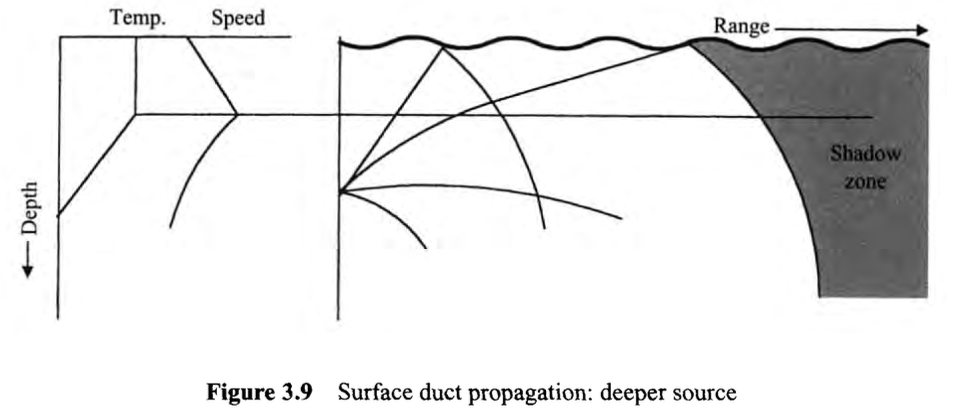
소음원이 위치한 깊이를 증가시켜 레이어 아래에 위치하도록 하면(그림 3.9) Shadow zone의 시작 범위를 미루는 효과가 있지만, 그 후 덕트까지 확장될 수 있다. DSC 및 RAP 모드와 마찬가지로 이동 중인 수상함이나 호버링 헬리콥터에서 배치한 가변 수심 소나(VDS)를 통해 심해에서 음파를 던지게 한다면 상당한 작전상의 이점을 제공합니다.

Convergence Zone Propagation

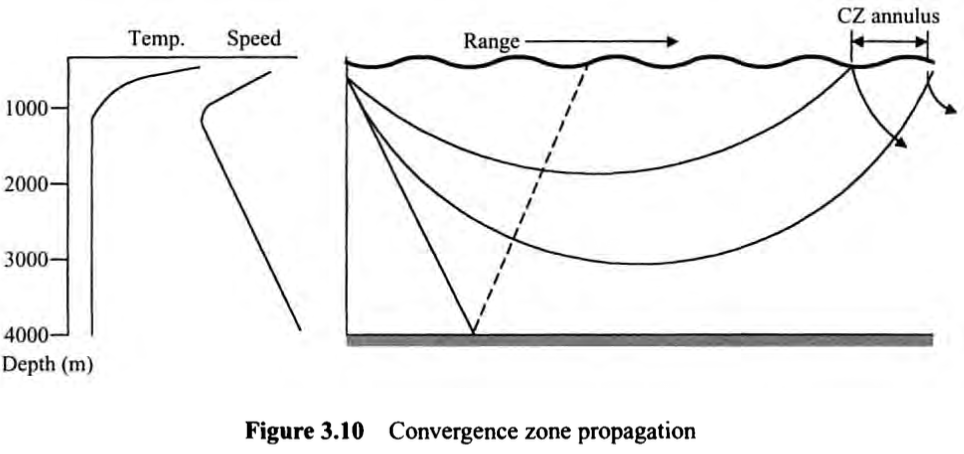
5도 이상의 각도로 발사된 음파는 최초에는 밑으로 휘어진다. 이때 Shadow zone을 형성한다. 그리고 더 깊은 곳에서는 압력이 이 음파를 위쪽으로 위어지게 한다. 이때 높은 강도의 갈고리 모양을 그리게 된다(그림 3.10). 각각의 갈고리는 Convergence Zone이라고 한다.
음파가 바다에 부딪혀서 돌아오는 것은 좋은 형태가 아니기에 이런 갈고리 모양이 형성되는 것이 바람직하다. 하지만 이런 효과가 생기기 위해서는 수심이 3000m 이상이 되어야 한다. 수심에 따라 Convergence Zone이 생기고 이것은 수심의 깊이에 따라 30~50km에서 생기고 그 넓이는 3~5km 정도이다.

Propagation은 구형의 형태를 띈다(장애물이 없다면). 흡수 손실은 약 4°C(대부분의 경로에 걸친 온도)에서의 손실으로 보며, 초점 효과로 인해 일반적으로 3~6dB의 수렴 이득이 발생한다.

연속적인 CZ는 최초의 범위의 배수에 존재한다. 능동형 소나의 경우에서 propagation losses에 의해 처음의 Convergence zone만들 사용할 수 있다. 하지만 수동 소나에서는 두번째 CZ, 심지어 세번째 CZ를 사용할 수 있다.
이유는 능동형 소나는 소리를 던지고 돌아오는 걸 받아야 감지를 할 수 있기에 두,세번째 CZ에 대한 신뢰도가 떨어질 수밖에 없고 수동형 소나는 돌아다는걸 받기 때문에 두,세번째 CZ를 받아낼 수 있는 것이다.

Bottom Bounce Propagation

해저면을 사용하여 Propagation이 가능할까요? 당연히 가능하다(그림 3.11). 소나빔은 이제 의도적으로 비교적 가파른 각도로 아래를 향해 쏜다. 이 방식의 효과는 해저면의 흡수성과 반사성 그리고 입사각에 따른 해저면 손실이 어떻게 되는냐에 따라 결정된다. CZ와 마찬가지로 소나 빔의 함몰 각도에 따라 고리의 범위가 달라지며 작은 입사각에서는 이것이 매우 넓어진다. 한 곳에 집중에서 소리를 쏘는 것의 이익은 Bottom Bounce Propagation 상황에서는 없고 해저면 반사 손실은 일반적으로 10~20dB이라 한다. 따라서 이 방식은 프로젝터 어레이의 크기를 설정하기 매우 까다롭다.

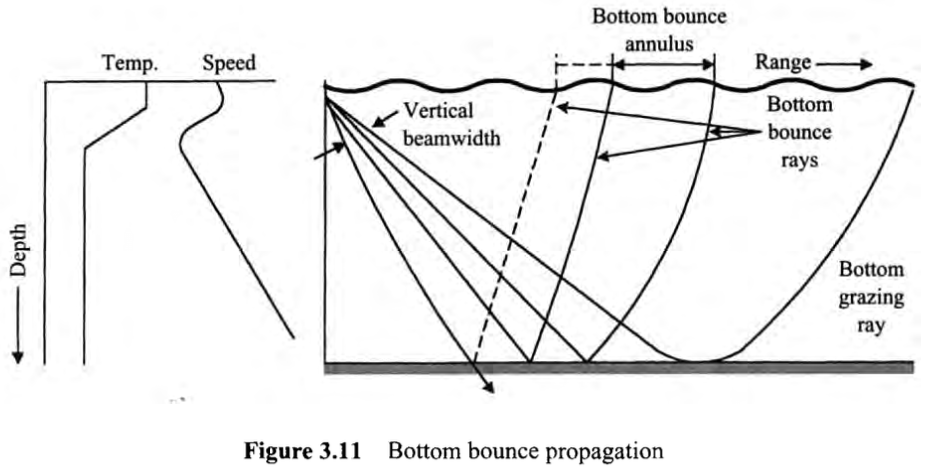
액티브 바텀 바운스(BB) 시스템은 크기가 커서 어레이를 설치하기 위한 넓은 부분이 필요하다. 연속적인 고리의 범위는 첫번째 고리의 배수로 존재한다. 전파 손실(양방향)로 인해 능동 시스템의 경우 첫 번째 고리 외에는 사용할 수 없지만 수동 시스템은 두 번째 고리의 범위에서 감지할 수 있으며, BB 모드의 범위 고리는 집중형 CZ 보다 훨씬 넓다. 수심과 소나 빔의 허용 함몰 각도(해저면 손실의 관점에서 허용되는 각도)에 따라 최소 10km 이상의 최소 범위까지 항상 Shadow zone이 있어야 한다.

Propagation Loss Models

지금까지는 바다에서 소리의 확산, 굴절 및 반사는 매우 간단하지만 종종 적절한 정량적 표현을 제외하고는 정성적인 방식으로만 논의을 했다. 탄성 매질에서의 소리의 전파는 특정 환경에 적합한 경계 및 매질의 조건을 활용하여 파동 방정식을 푸는 방식으로 수학적으로 설명할 수 있다.
이 방정식을 푸는 데는 두 가지 접근 방식이 있다.

• 파동 이론: 전파는 정상 모드라고 하는 특성 함수의 관점에서 설명되며, 각 모드는 방정식의 해다. 이 모드는 필요한 경계 조건과 중간 조건을 충족하기 위해 추가적으로 결합된다.
• 광선 이론: 이 이론은 파장과 음원의 소리가 어디로 가는지를 나타내는 광선의 존재를 가정한다. 파장의 곡률 반경이나 압력이 파장의 거리에 따라 크게 변하는 경우에는 좋은 솔루션을 제공하지 못한다. 따라서 짧은 파장으로 제한된다.

두 가지 접근법을 표 3.2에서 비교해보자.소나 모델링 핸드북(영국 국방부 DERA 발행)은 다양한 파동 이론 및 광선 이론 모델과 그 실제적 한계에 대한 유용한 정보를 제공하는 자료이다.

Ray Theory and the Hodgson Model

광선 이론은 호지슨 모델의 관점에서 설명한다. 이 모델은 영국 해군에서 작전용으로 사용되며 200Hz 이상의 주파수에서 적용 가능하다. 지정할 수 있는 소나 매개변수에는 주파수, 수심, 빔 최소 및 최대(수직) 각도가 있다.
해면은 주파수 및 표면 거칠기(해상 상태, 풍속 또는 파도 높이 입력 가능)에 따라 광선이 바운스당 감쇠되는 반사판으로 모델링된다. 해저면 손실은 일련의 해저면 손실 곡선을 사용하여 계산되며, 바운스당 손실은 주파수와 방목 각도에 따라 달라진다. 흡수 손실은 주파수, 온도, 수심, 염분의 함수로 정확하게 모델링되며 각 광선의 범위에 따라 지속적으로 변경된다.
음속 필드는 깊이와 범위에서 SSP를 보간하여 계산한 다음, 환경을 깊이에 따라 음속이 선형적으로 변하는 일련의 상자로 분할한 후 스넬의 법칙을 사용하여 광선 경로를 계산한다(그림 3.12). 이것이 범위 종속 솔루션이 도출되는 방식이다.

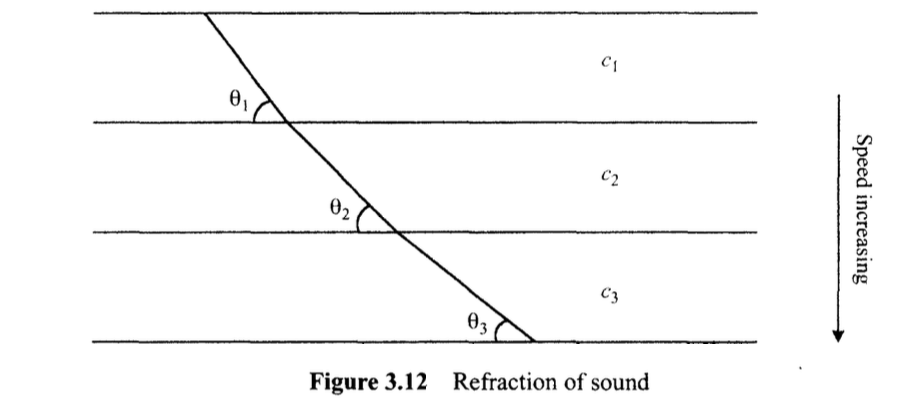
Snell's law

스넬의 법칙은 광선 이론 모델의 기본이며, 음속이 변화하는 매질에서 음파의 굴절을 설명한다. 음속이 깊이에 따라 지속적으로 변하는 경우, 매질은 그 안에 음속이 일정하지만 서로 다른 여러 개의 얇은 층으로 이루어진 것으로 간주할 수 있다. 각 층의 경계에는 스넬의 법칙이 적용되어 음파가 곡선을 그리는 것으로 볼 수 있다.

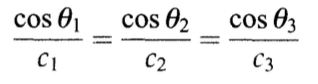
깊이에 따라 속도가 계속 증가하면 광선은 수평이 되고 cose = 1이 된다. 광선이 수평인 경우의 음속인 cv를 정점 속도라고 한다.

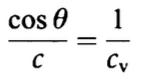
이 방정식을 사용하면 속도 프로파일이 분할된 레이어를 통과하는 광선의 경로를 생성할 수 있다.

Hodgson Example

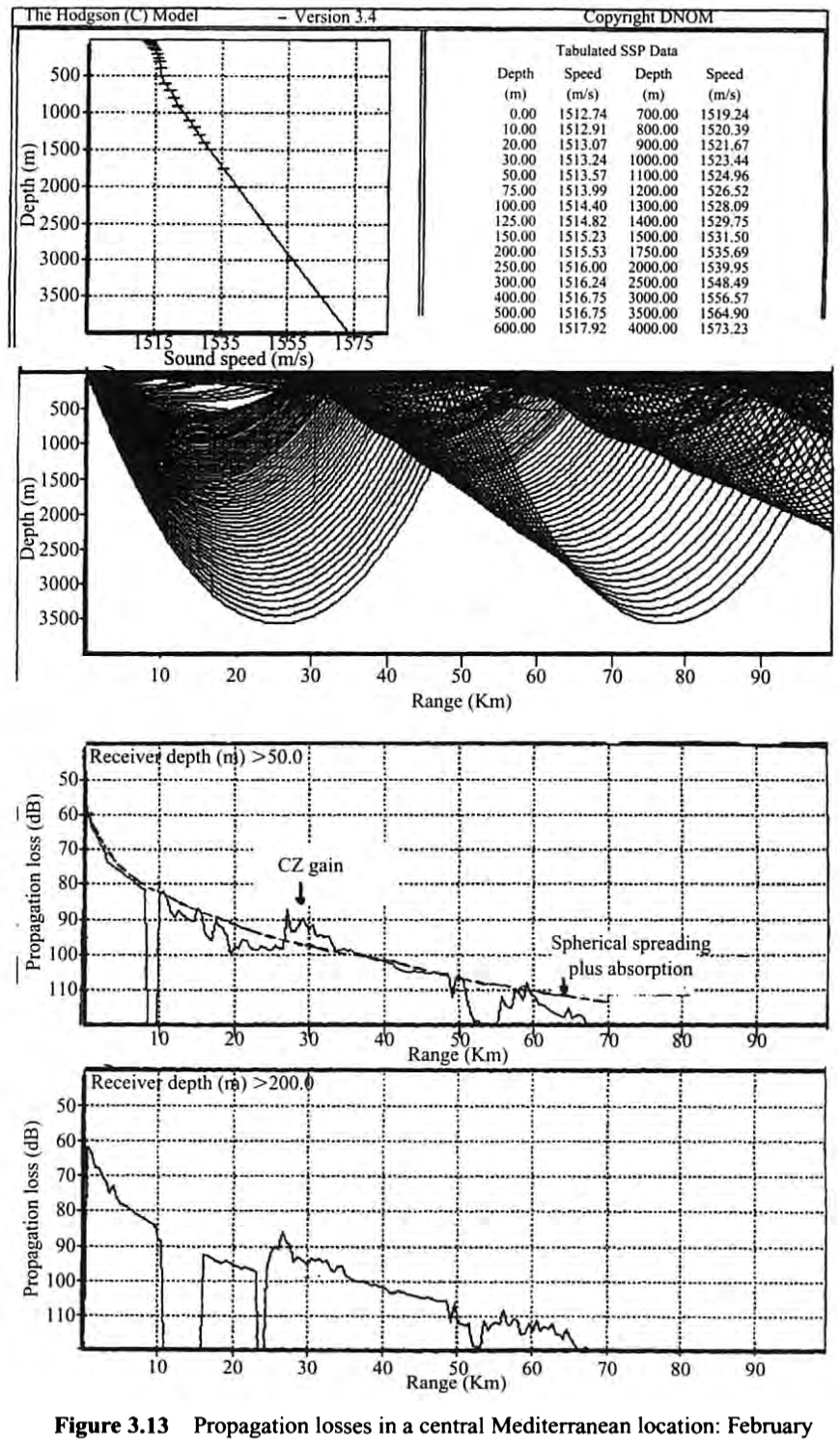
지중해 중부 지역에서의 Propagation 손실은 2월(그림 3.13)과 8월(그림 3.14)을 보면 알 수 있다. 주파수는 5kHz이고 소나 수직 빔 폭은 0-15도이며 수심은 5m다.

2월
광선 추적은 약 8km에서 25km 사이의 그림자 영역을 보여주며, 이는 두 수신기 수심 50m와 200m의 PL 곡선에서 분명하게 나타난다. 특히 그림자 영역을 제외하면 구형 확산 + 흡수의 간단한 법칙이 모델 예측을 매우 정확하게 따른다는 점에 유의하라. 약 30km를 중심으로 손실이 줄어든 것은 CZ 이득이 발생했기 때문이다.

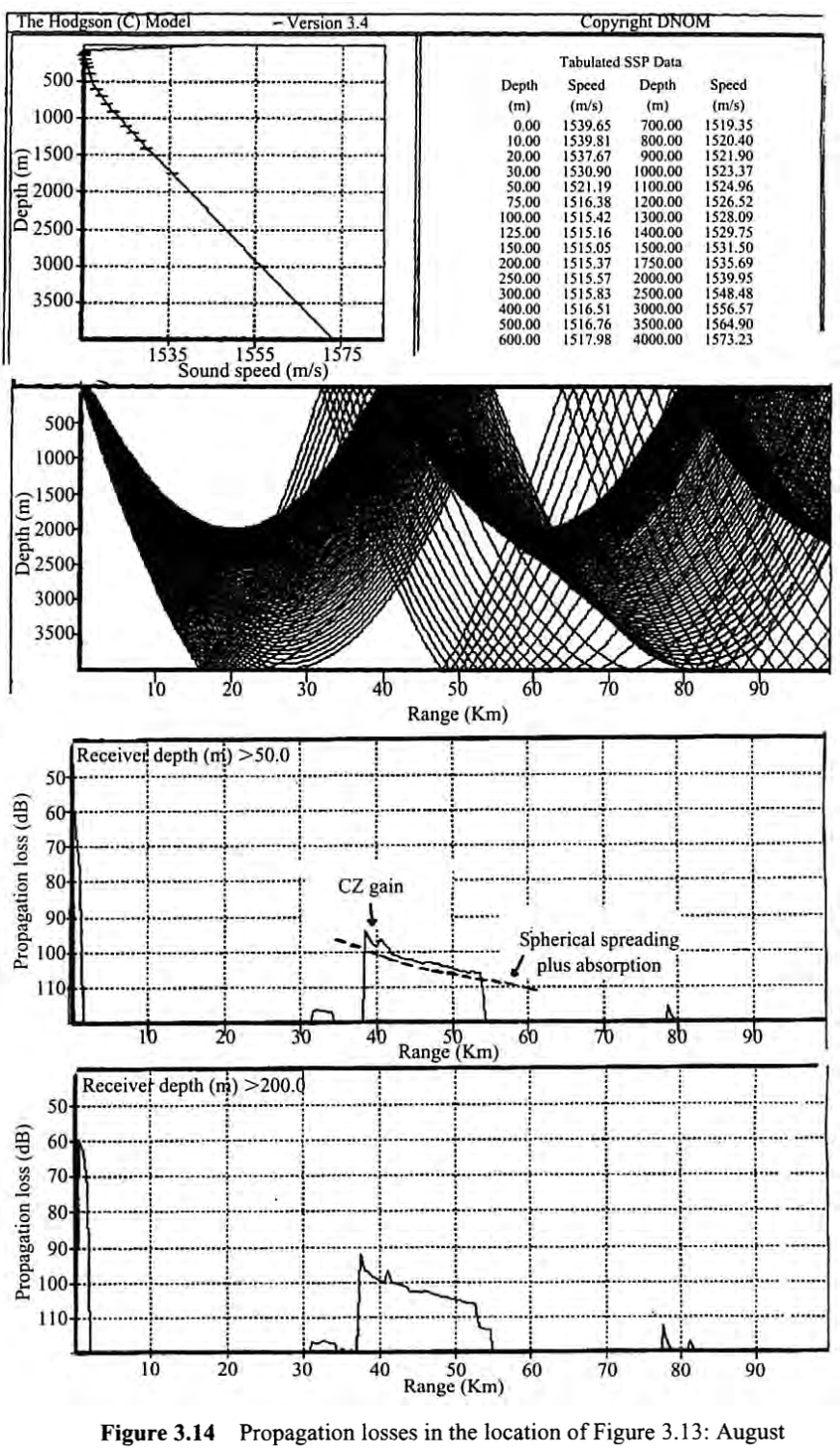
8월
지표면 근처에서 심한 하향 굴절이 발생하여 약 40km를 중심으로 약 2km에서 CZ가 복귀할 때까지 그림자 영역이 발생하며, 첫 번째 BB 복귀와 두 번째 CZ 복귀에 주목한다.(각 방향 110dB 이상에서는 액티브 시스템으로는 손실이 너무 크지만 패시브는 가능한 경우도 있음).

Performance Prediction

전파 손실은 소나 시스템의 탐지 성능을 예측하는 데 필요한 여러 파라미터 중 하나이다. 소스 레벨(SL) 및 지향성 지수(DI)와 같은 파라미터는 2dB 이내로 상당히 정확하게 알려져 있지만 전파 손실(PL)은 매우 가변적이며, 모델이 아무리 정확하고 환경을 잘 표현하더라도 입력 데이터만큼만 좋은 결과를 얻을 수 있다.

운영 조건에서는 제한된 수의 지점에서만 SSP를 측정할 수 있으며, 일반적으로는 소나 플랫폼 자체에서 한 지점만 측정할 수 있다. 이 SSP는 소나와 목표물 사이의 모든 물기둥에 정확하게 적용되지는 않는다.

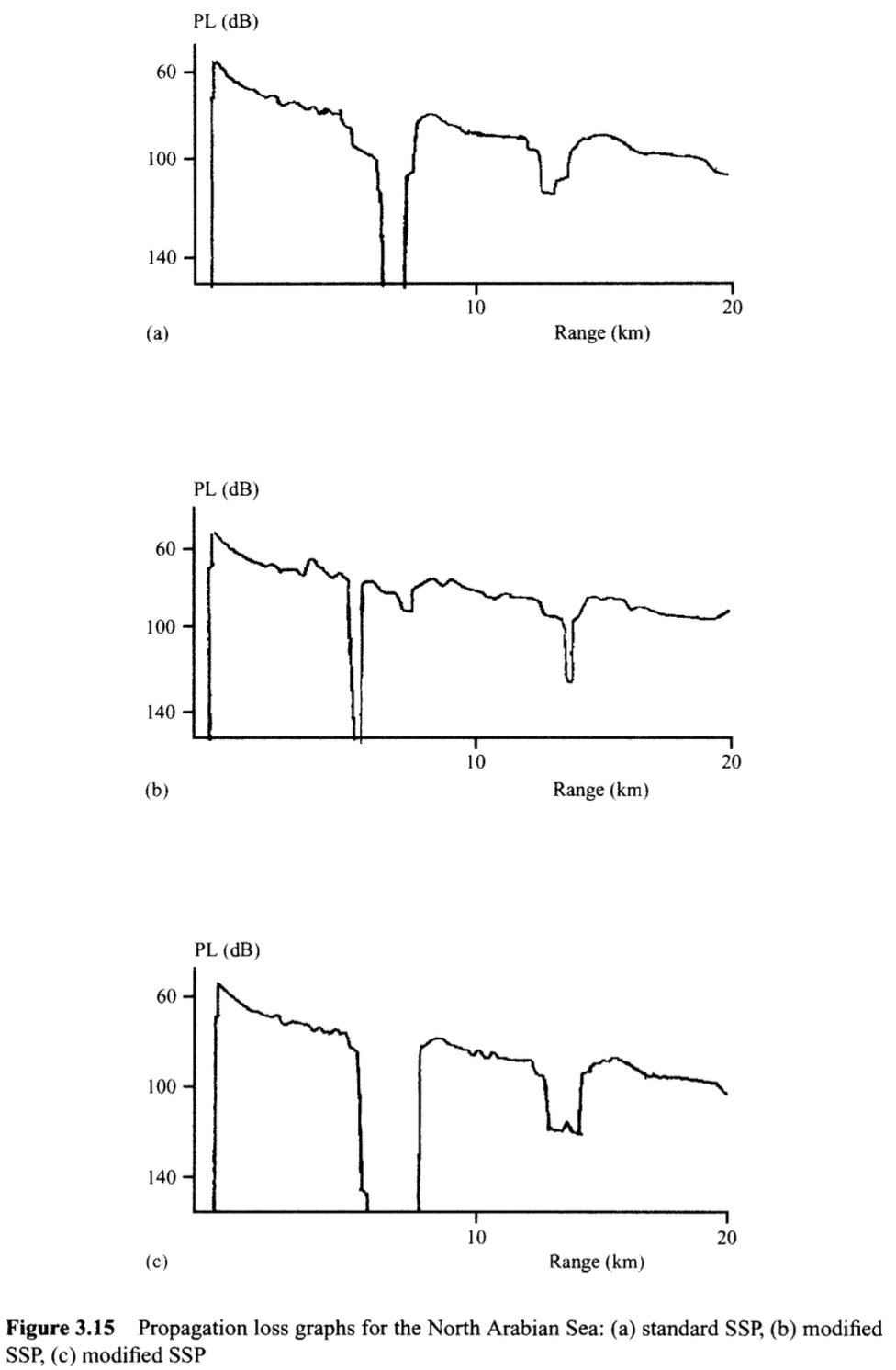
PL 그래프는 주로 수심 대비 온도 측정에 의존하는 SSP에 크게 의존한다. 그림 3.15의 PL 그래프는 온도 측정의 아주 작은 부정확성, 즉 수온계에서 흔히 볼 수 있는 부정확성에 대한 차이를 보여준다.

모든 그래프는 2월 중 북아라비아해의 한 지역에 대한 것이다. 2월의 '표준' SSP는 그림 3.15(a)를 산출한다. 이 SSP를 수정하여 가능한 수온계 오차를 나타내면 그림 3.15(b)와 (c)가 나온다. 그림 3.15(b)는 수심 75m까지의 모든 속도 값에서 1m/s를 빼고 다른 모든 값에 1m/s를 더하면 구할 수 있다. 그림 3.15(c)는 수심 75m까지의 모든 속도 값에 1m/s를 더하고 다른 모든 값에서 1m/s를 빼면 구할 수 있다.

세 그래프 모두 매우 유사하지만 세부적으로 보면 상당한 차이가 있다.
이는 전파 모델의 결과에 암묵적으로 의존하는 것의 위험성을 보여준다. 100dB의 전파 손실이 주어진 소나 시스템에 허용되는 손실(탐지가 가능한 손실)이라고 가정하면 해당 범위 한계는 상당히 달라진다.

Multipath Propagation

수중 소리의 전파는 항상 수직면에서 여러 경로를 따른다. 이는 수직 빔폭이 유한하기 때문에 불가피한 결과이며, 가능한 경로에 따라 도착 시간과 전파 손실에 차이가 발생한다. 이러한 차이는 소스에서 수신기까지의 거리가 멀어질수록 증가한다.
이러한 차이에 대한 정량적 지식이 중요하다. 능동형 소나 시스템에서 큰 차이는 시간(범위)이 분리된 여러 개의 에코를 생성할 수 있고, 작은 차이는 표적의 신장을 생성할 수 있다. 패시브 소나 시스템에서는 도착 시간 간의 차이가 범위를 추정하는 데 사용된다. 다중 경로 전파에 대해서는 이후에 설명하겠다.

오늘은 Propagation of Sound in the Sea에 대해 살펴왔다. 바다 안에서 음파가 전파될 때 어떤 영향을 받게 되고 어떻게 전파되는지 알게 되었을 것이다. 내용이 방대하긴 했지만 이전에 다뤘던 내용보다는 보다 직관적이었으니 계속 보다보면 쉽게 이해가 될 것이다. 이제 끝. 해산.