Backpropagation 사용이유
우리가 머신러닝, 딥러닝을 공부하면 백프로파게이션이라는 단어를 많이 들어봤을 것이다. 왜냐하면 딥러닝, 머신러닝에서 굉장히 중요한 부분을 차지하고 있기 때문이다.
그래서 우선 왜 backpropagation을 사용해야 하는지에 대해 알아보겠다.
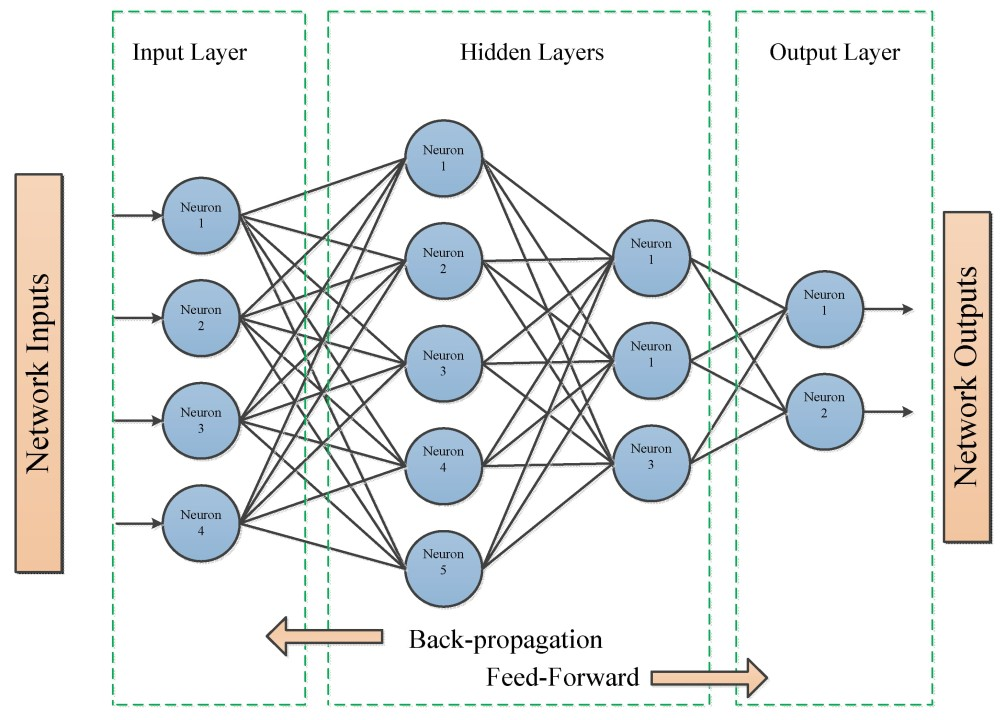
딥러닝에서는 다음과 같은 구조를 가지고 있다.
입력층 -> 은닉층 -> 출력층
여기서 우리는 입력값과 각각의 파라미들을 통해서 결과를 얻게 된다.
여기서 결과가 옳바른지 아닌지를 판단하는 것은 이미 알고 있는 정답과 비교해서 오차를 구하는것이다.
우리가 오차를 구할때 흔히 사용하는게 MSE(오차제곱의 합)이다.
만약에 실제 데이터와 딥러닝을 통해 구한 결과의 오차인 MSE가 크다면 어떻게 해야할까?
궁극적으로 그 오차가 0이면 정답인것이다. 그리고 100프로 정답이 아니더라도, 그 오차를 최소화한다면 해당 모델이 잘 학습했다고 생각하면된다.
그래서 우리는 이 오차함수를 최소화 해야한다.
그럼 오차 함수를 어떻게 최소화 하느냐??
바로 optimization 개념이 도입된다.
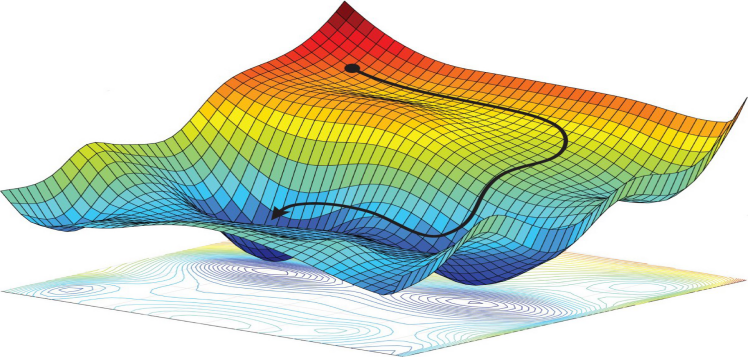
우선은 optimization 함수는 간단하게 다음과 같이 나타난다.
해당 그래프가 우리의 오차함수라고 생각하면된다. 그리고 오차를 최소화한다는게, 오차함수의 최소값을 찾는 문제로 치환된다.
그래서 optimziation은 해당 함수에서 최소값을 잘 찾아주는 개념이라고 생각하면 된다.
아무튼, 이런 optimization 함수를 사용해서 최적의 파라미터들을 구해야하는데, 한가지 문제점이 있다.
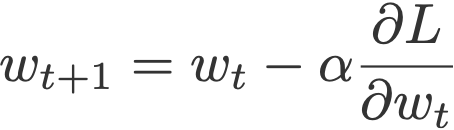
바로 이게 optimization에서 가장 기초가 되는 SGD optimization의 공식인데, 여기서 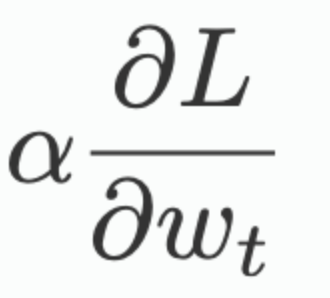
해당 식에 집중을 해야한다.
이게 바로 우리가 고등학교 떄 배운 미분이다.
즉 어떤 함수에 대해서 파라미터로 미분하고 알파만큼의 값을 곱해서 기존의 파라미터를 수정하는 방식으로 진행된다는 것이다.
그래서 해당 함수에 대한 파라미터의 미분.
즉, 각각의 파라미터가 각각의 함수에 어느정도 영향을 미치는가.
다시 말해 파라미터가 변할떄, 오차 함수가 얼마나 변하느냐?
를 알면 우리가 파라미터를 계속 바꿔가면서 오차함수를 가장 줄일수 있는 파라미터를 찾게되는것이다.
그래서 우리는 백프로파게이션이라는 개념을 통해서 수많은 파라미터들이 최적의 값을 갖도록 조절할 것이다.
Chain Rule
backpropagation에서 중요한 개념은 바로 체인룰이다.
우리가 미분을 배웠다면 모두 체인룰을 적용하고 있을것이다.
예를들어 보면
ex) 을 x에 대해 미분한다고 생각해보자. 이걸 미분하면 가된다.
을 F 라고 가정해보자
우리가 어떻게 계산을 했는가?
바로 를 F 에 대해 미분하면 2F.
을 x로 미분해서 4x 가 된다.
즉 이둘을 곱해 가 된다.
이게 바로 체인룰이다.
이제 이걸 DeepNN에 도입해보자.
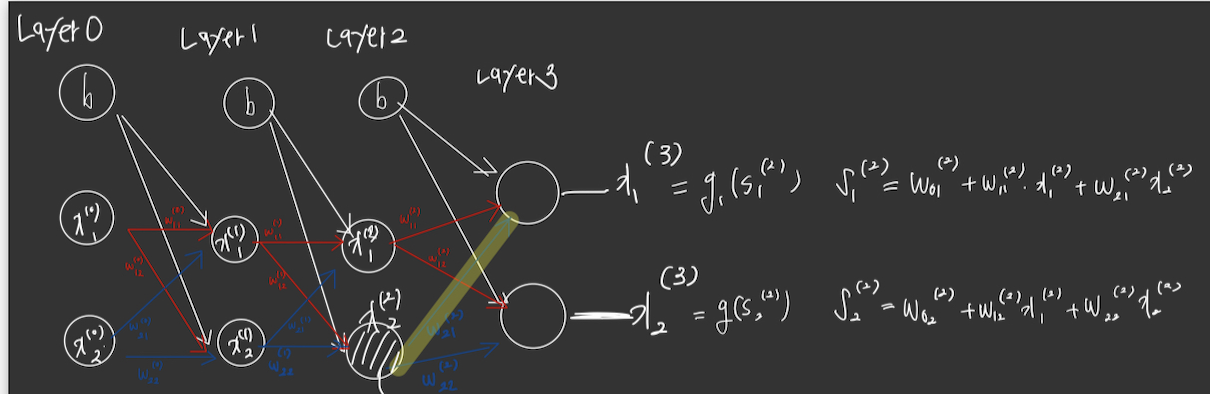
위의 그림에서 변수 위의 값들은 레이어 층을 의미하고,
변수 아래 써있는건 N번쨰 값에서 M번째 값으로 이동하는것이다.
그리고 x는 각 노드의 값들, s는 activation함수를 지나기 전의값 이라고 가정한다. 식이 복잡하다면 마지막 결과만 봐도 좋다.
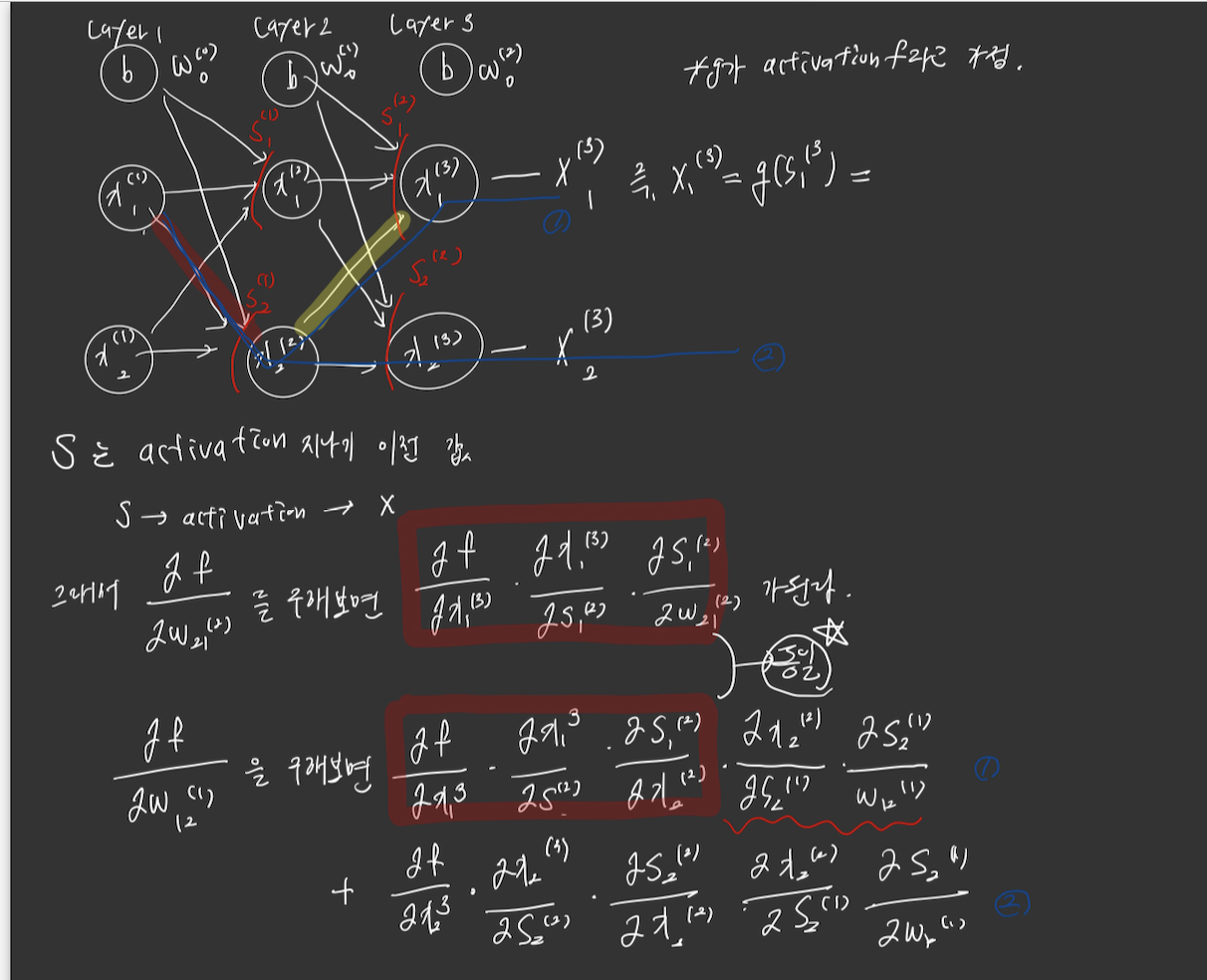
결국에는 첫번째 식이 노란색 선의 파라미터를 구한것이고,
두번째 식이 빨간색 선의 파라미터를 구한것이다.
여기서 이 두개의 식을 봤을떄, 공통적으로 사용된것이 보일것이다.
바로 노란색의 파라미터 값이다.
빨간색의 파라미터는 그럼 간단하게 노란색파라미터의 변화량 * 해당 노드의 파라미터변화량만 계산해주면, 의 값에 빨간색 파라미터가 얼마나 영향을 미치는지를 알수 있다는 것이다.
즉! 이전노드까지의 변화량 (미분값)만 가지고 있다면, 현재 노드에서의 미분값만 구해서 곱해주면 전체 적인 변화량을 구할수 있다는 개념이다.
Deep NN에서 엄청난 수의 파라미터가 있지만 결국, 각각의 파라미터들에 대한 미분값만 구해준다면 모든 파라미터에 대한 변화량을 얻을수 있고, 결국 파라미터의 최적의 값을 구할수 있다는 것이다.
Backpropagation
결국 backpropagation은 체인룰에 의해서 파라미터를 수정하는것이다.
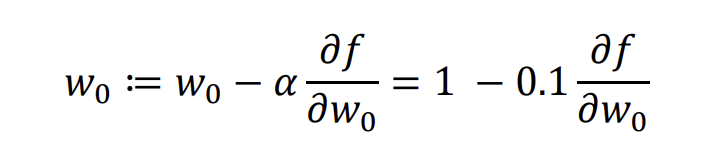
다음 그림처럼 간단하게 해당 노드에서의 변화량을 이용해서 해당 파라미터를 수정하는것이다.
