프로그래머스 n으로표현 자바

문제링크

N으로 표현

문제분석

처음에는 "N은 1 이상 9 이하입니다"라는 조건을 보고 dfs를 풀어야겟다고 생각했다. dfs로 풀어 정답을 맞출 수 있었지만 테스트케이스를 생각하던 중 26에서 문제가 발생했다.
5x5+(5/5) = 26 최소 4개로 26을 만들수 있지만 dfs의 경우 최소 5개로 해결되어 해당 문제의 정답 케이스가 잘 못 되었다고 판단이 되었다. 그래서 다른 사람들의 코드들을 보며 dp로 푸는 방식이 해당 문제에 정확한 코드인 것을 알게 되었고 풀이과정을 남기면 정확하게 기억해두고 싶었다.

dfs가 되지 않는 이유는 5x5+(5/5) 로 계산되어야할 해당부분이 5x5->(5x5+5)->(5x5+5)/5 방식으로 계산이 된다. 그래서 항상 앞부분의 결과값으로 계산이 되기때문에 만족되지가 않는다

풀이과정

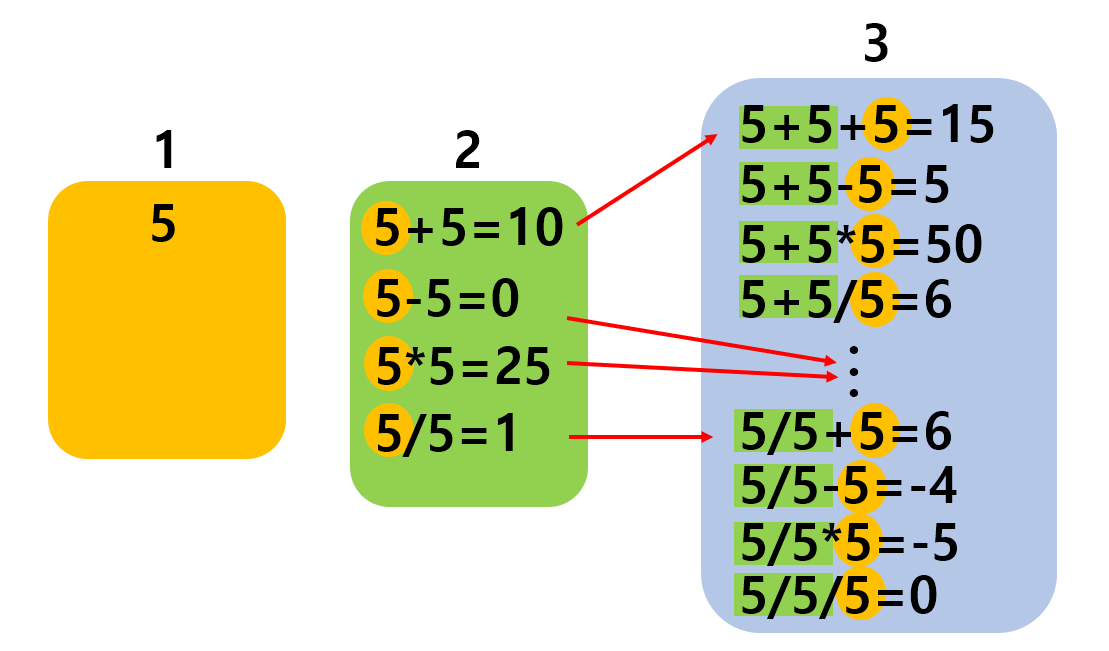
1. n의 사용횟수 기준으로 풀기

   • n의 사용횟수에 따른 연산값이 중복해서 들어가지 않도록 set리스트를 사용

2. N을 1번 사용해서 만들수 있는 수의 집합은 N

3. N의 사용횟수가 최소 8번 이하의 사칙연산으로 최소값 찾기

   3.1 N을 1번 사용할 경우 들어갈 수 있는 수 =

   • N(자신)

   3.2 N을 2번 사용할 경우 들어갈 수 있는 수 =

   • 1번 연산('+','-','/','*') 1번

   3.3 N을 3번 사용할 경우 들어갈 수 있는 수 =

   • 1번 연산 2번, 2번 연산 1번

   3.4 N을 8번 사용할 경우 들어갈 수 있는 수 =

   • 1번 연산 7번, 7번 연산 1번
   • 2번 연산 6번, 6번 연산 2번
   • 3번 연산 5번, 5번 연산 3번
   • 4번 연산 4번

3.5 N의 사용횟수마다 연속된 숫자 넣기

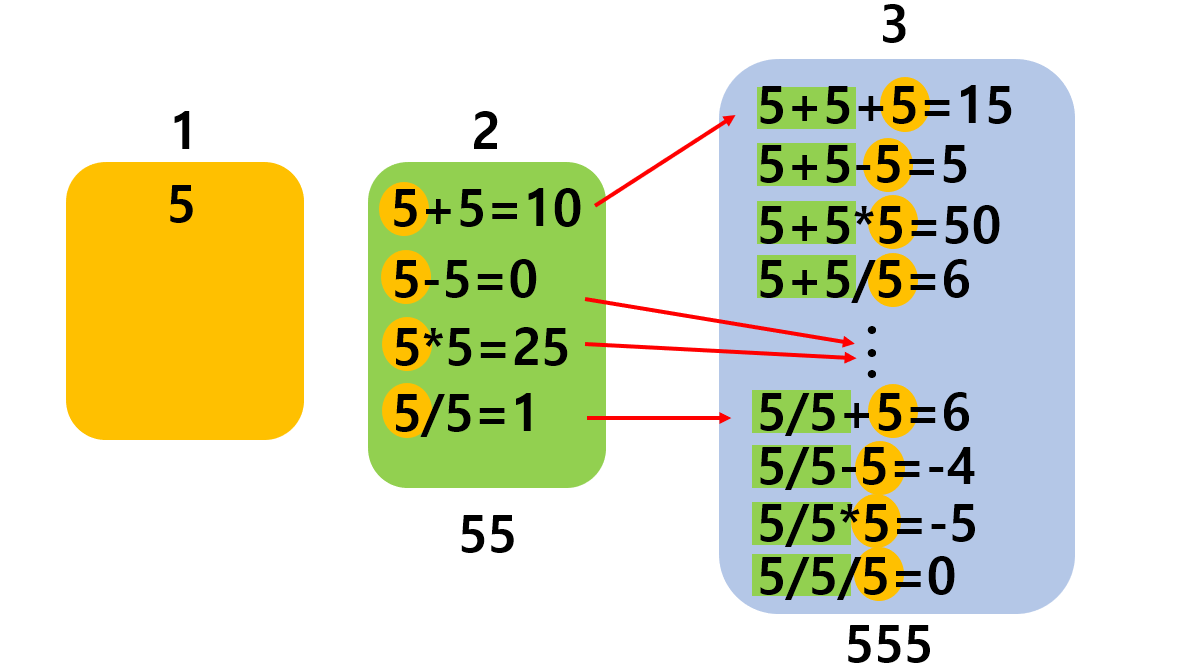
⛳ 내가 작성한 코드

import java.util.*;
public class AN으로표현 {
	
	public static void main(String[] args) {
		int N = 2;
		int number = 11;
		// 1. n의 사용횟수에 따른 연산값이 중복해서 들어가지 않도록 set리스트를 사용
		Set<Integer>[] numberBox = new HashSet[9];
		for(int i=1; i<9; i++) {
			numberBox[i] = new HashSet<>();
		}
		
		// 2.N을 1번 사용해서 만들수 있는 수의 집합은 N
		numberBox[1].add(N);
		
		// 3.최소값 구하기
		int answer = getAnswerMinCount(N,number, numberBox);
		System.out.println(answer);
		
	}
	
	private static int getAnswerMinCount(int N, int number, Set<Integer>[] numberBox) {
		for(int i=1; i<9; i++) {
			for(int j=1; j<i; j++) {
				// 3. n의 사용횟수에 대한 사칙연산한 값 넣기
				isCalculateNumbers(numberBox[i], numberBox[i-j], numberBox[j]);
			}
			
			// 3.5 N의 연속된 숫자 넣기
			String continuousNumber = Integer.toString(N).repeat(i);
			numberBox[i].add(Integer.parseInt(continuousNumber));
			// 해당 박스안에 number가 있다면 사용횟수 반환
			if(numberBox[i].contains(number)) {
				return i;
			}
		}
		
		//최소 8번으로 답이 나오지 않을경우
		return -1;
	}
	
	private static void isCalculateNumbers(Set<Integer> union, Set<Integer> cal1, Set<Integer> cal2) {
		for(int x: cal1) {
			for(int y: cal2) {
				union.add(x+y);
				union.add(x-y);
				union.add(x*y);
				if(y!=0) union.add(x/y);
			}
		}
	}
}