
✏️ 문제
현호는 사내 네트워크 분석 업무를 담당하게 되었다. 현재 사내 네트워크는 N개의 노드를 가지는 트리 형태의 네트워크인데, 이 말은 두 노드간의 연결이 정확히 N-1개 있어서 이 연결만으로 모든 노드간에 통신을 할 수 있다는 뜻이다.
각 노드에 1에서 N사이의 번호를 붙이면 i번째 연결은 xi번 노드와 yi번 노드를 양방향으로 연결하며, 통신에 걸리는 시간은 ti이다. D(i,j)는 i번 노드와 j번 노드 사이의 거리를 나타내는데, i번 노드에서 여러 연결을 거쳐 j번 노드에 도달하기 위해 걸리는 최소 시간이다.
노드를 들를 때 추가적인 작업이 없는 이상적인 시간을 따진다. 현호는 네트워크 분석을 위해 어떤 노드 i를 기준으로 다른 모든 노드 사이와의 거리의 합을 알고 싶다. 즉, 을 알고 싶다.
입력예제 2번을 예로 들면, 다음과 같이 7개의 노드로 이루어진 네트워크로 표현할 수 있다. 각 연결 위에 적힌 수는 t를 나타낸다.
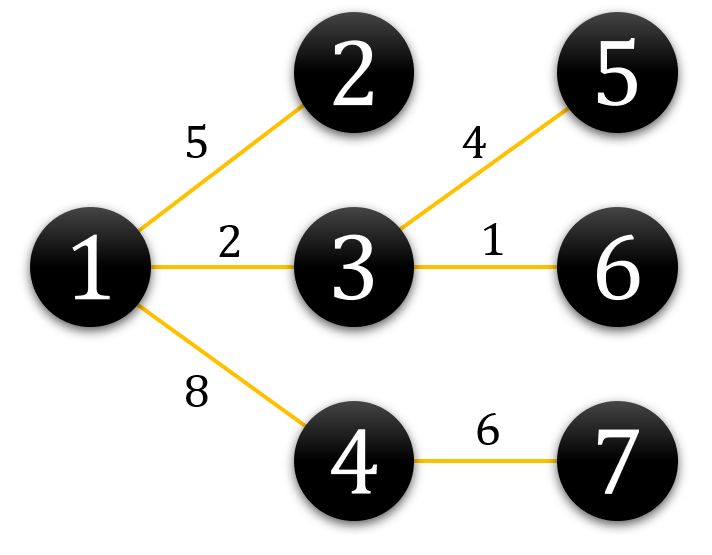
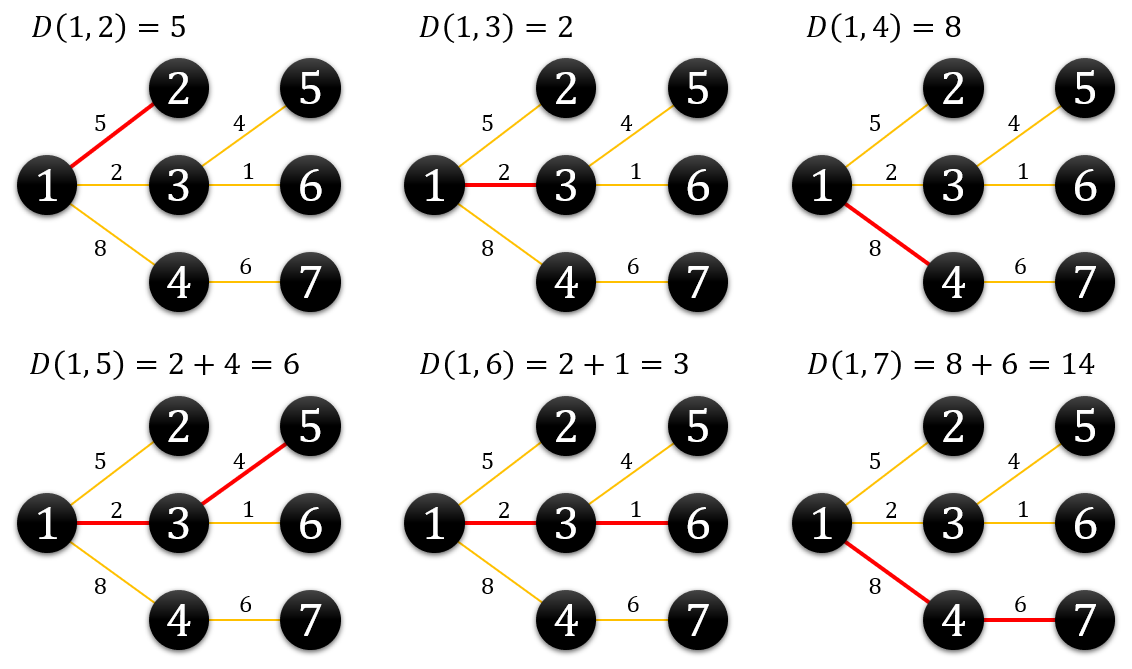
1번 노드를 기준으로 D(1,j)를 구해보면 다음과 같다.
⛔️ 제약조건
1≤N≤2×105
주어진 N-1개의 연결로 모든 노드가 연결되어 있다.
1≤xi,yi≤N
1≤ti≤106
🎈 입력형식
첫 번째 줄에 노드의 개수 N이 주어진다.
다음 N-1줄의 i번째 줄에는 i번째 연결을 나타내는 세 정수 xi,yi,ti가 주어진다.
🎈 출력형식
N개의 줄에 걸쳐서, i번째 줄에는 i번 노드와 다른 모든 노드 사이의 거리의 합,
를 출력한다.
🎈 입출력 예
- 입력
4
1 2 1
2 3 2
3 4 4- 출력
11
9
9
7
👩💻 내 코드 - DFS (오답, 시간초과)
이 문제는 n의 범위가 20만까지라서 어떻게 풀어야 할지 고민을 많이 했다. 일단 dfs로 풀어보았지만 역시나 시간초과가 났다.
#include<iostream>
#include<vector>
using namespace std;
struct NODE {
int node, cost;
};
vector<NODE> graph[200001];
int n, sum;
int answer;
void input() {
cin >> n;
// 그래프 구성
for (int i = 0; i < n-1; i++) {
int from, to, cost;
cin >> from >> to >> cost;
graph[from].push_back({to, cost});
graph[to].push_back({from, cost});
}
}
void dfs(int now, int before, int sum) {
answer += sum;
for (int i = 0; i < graph[now].size(); i++) {
int next = graph[now][i].node;
int nextcost = graph[now][i].cost;
if (before == next) continue;
dfs(next, now, sum + nextcost);
}
}
int main(int argc, char** argv)
{
input();
for (int i = 1; i <= n; i++) {
sum = 0;
answer = 0;
dfs(i, 0, 0);
cout << answer << '\n';
}
return 0;
}👩💻 내 코드 - DFS (오답)
시간초과는 사라졌지만 여전히 오답인 코드.
어디서 틀렸는지 디버깅을 해봐야겠다.
#include <iostream>
#include <vector>
using namespace std;
struct NODE {
int node, cost;
};
vector<NODE> graph[200001];
int subtree[200001];
int sum[200001];
int n;
void input() {
cin >> n;
for (int i = 0; i < n-1; i++) {
int from, to, cost;
cin >> from >> to >> cost;
graph[from].push_back({to, cost});
graph[to].push_back({from, cost});
}
return;
}
void dfs2(int now, int before) {
for (int i = 0; i < graph[now].size(); i++) {
int next = graph[now][i].node;
int nextcost = graph[now][i].cost;
if (next != before) {
sum[next] = sum[now] + nextcost * (n-2*subtree[next]);
dfs2(next, now);
}
}
return;
}
void dfs1(int now, int before) {
subtree[now] = 1;
for (int i = 0; i < graph[now].size(); i++) {
int next = graph[now][i].node;
int nextcost = graph[now][i].cost;
if (next != before) {
dfs1(next, now);
sum[now] += sum[next] + subtree[next] * nextcost;
subtree[now] += subtree[next];
}
}
}
int main() {
input();
dfs1(1, 1);
dfs2(1, 1);
for (int i = 1; i <= n; i++) {
cout << sum[i] << '\n';
}
return 0;
}