
✏️ 문제
루트가 있는 트리(rooted tree)가 주어지고, 그 트리 상의 두 정점이 주어질 때 그들의 가장 가까운 공통 조상(Lowest Common Anscestor)은 다음과 같이 정의됩니다.
- 두 노드의 가장 가까운 공통 조상은, 두 노드를 모두 자손으로 가지면서 깊이가 가장 깊은(즉 두 노드에 가장 가까운) 노드를 말합니다.
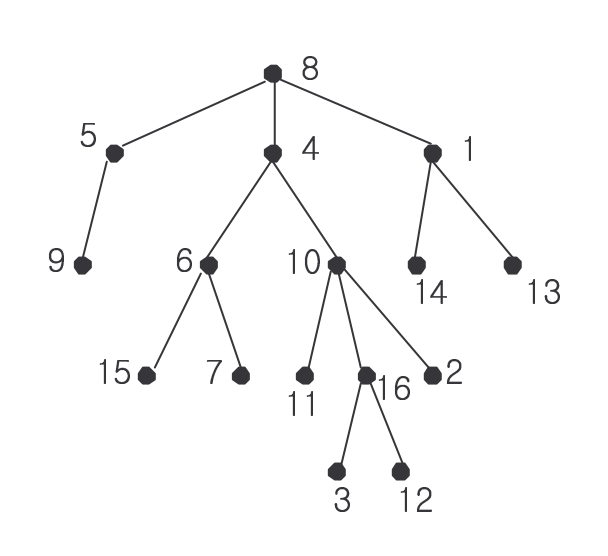
예를 들어 15와 11를 모두 자손으로 갖는 노드는 4와 8이 있지만, 그 중 깊이가 가장 깊은(15와 11에 가장 가까운) 노드는 4 이므로 가장 가까운 공통 조상은 4가 됩니다.
루트가 있는 트리가 주어지고, 두 노드가 주어질 때 그 두 노드의 가장 가까운 공통 조상을 찾는 프로그램을 작성하세요
🎈 입력
첫 줄에 테스트 케이스의 개수 T가 주어집니다.
각 테스트 케이스마다, 첫째 줄에 트리를 구성하는 노드의 수 N이 주어집니다. (2 ≤ N ≤ 10,000)
그리고 그 다음 N-1개의 줄에 트리를 구성하는 간선 정보가 주어집니다. 한 간선 당 한 줄에 두 개의 숫자 A B 가 순서대로 주어지는데, 이는 A가 B의 부모라는 뜻입니다. (당연히 정점이 N개인 트리는 항상 N-1개의 간선으로 이루어집니다!) A와 B는 1 이상 N 이하의 정수로 이름 붙여집니다.
테스트 케이스의 마지막 줄에 가장 가까운 공통 조상을 구할 두 노드가 주어집니다.
🎈 출력
각 테스트 케이스 별로, 첫 줄에 입력에서 주어진 두 노드의 가장 가까운 공통 조상을 출력합니다.
🎈 입출력 예
<입력>
2
16
1 14
8 5
10 16
5 9
4 6
8 4
4 10
1 13
6 15
10 11
6 7
10 2
16 3
8 1
16 12
16 7
5
2 3
3 4
3 1
1 5
3 5
<출력>
4
3
👩💻 내 코드
처음 문제를 풀 땐 Union Find 알고리즘으로 접근을 했다. 가장 먼 조상을 구하는 방법은 알지만 가장 가까운 조상을 구하는 아이디어는 생각이 나지 않아 결국 구글링의 도움을 받았다.
이 문제는 대표적인 Lowest Common Ancestor(LCA) 문제이다. 검색해보면 해당 알고리즘의 설명이 잘 나와있음.. 참고로 난 이 곳의 도움을 받아 문제를 풀었다.
import sys
sys.setrecursionlimit(10**6) # 재귀 깊이 제한 설정
def dfs(node, level):
visited[node] = 1
depth[node] = level
for next in graph[node]:
if visited[next] == 1:
continue
dfs(next, level+1)
def lca(a, b):
while depth[a] != depth[b]:
if depth[a] > depth[b]:
a = parent[a]
else:
b = parent[b]
while a != b:
a = parent[a]
b = parent[b]
return a
if __name__ == "__main__":
T = int(input())
for _ in range(T):
N = int(sys.stdin.readline())
parent = [0] * (N+1)
depth = [0] * (N + 1)
visited = [0] * (N + 1)
graph = [[] for _ in range(N+1)]
for _ in range(N-1):
a, b = map(int, input().split())
graph[a].append(b)
parent[b] = a
for i in range(1, N+1):
if parent[i] == 0:
dfs(i, 0)
break
find_a, find_b = map(int, input().split())
print(lca(find_a, find_b))
💡 새롭게 배운 것
- Lowest Common Ancestor 알고리즘
- setrecurtionlimit(10**6) : 파이썬 기본 재귀 깊이는 1000으로 제한되기 때문에 꼭 써야됨!
이 문제를 풀며 새로운 것을 많이 알게 되었다. LCA 알고리즘은 다른 문제를 더 풀며 연습해봐야겠다.
