💡 알고리즘을 학습하기에 앞서 기초적인 알고리즘의 성능을 평가하는 방법에 대해서 배워보자.

개요 🛫

---

시간 복잡도는 알고리즘, 자료구조에서 빠지지 않고 나오는 개념인데. 나는 제대로 공부해본 적이 없으므로..

기초부터 다져가며 공부해보자. 👍🏽

더 효율적인 알고리즘을 짜기 위해 알아야하는 필수적인 지식이라고 생각한다.

학습 내용 📖

---

5가지 알고리즘 성능 평가 지표

• 정확성
• 작업량
• 메모리 사용량
• 최적성
• 효율성 : 시간 복잡도 / 공간 복잡도

실제 알고리즘을 시험(코딩 테스트 등)하는 과정에서는 메모리 사용량과 효율성(시간 복잡도)를 우선적으로 평가한다.

---

시간 복잡도 ?

정의

입력 크기에 값에 대해 단위 연산을 몇 번 수행하는지 계산하여, 알고리즘의 수행시간을 평가하는 방법.

3가지 표현법

• O(빅오, Big-O) : 최악의 상황을 고려한 성능 측정 결과 표현법
• θ(세타, Theta) : 평균적인 경우의 성능 측정 결과 표현법
• Ω(오메가, Omega): 최선의 상황을 고려한 성능 측정 결과 표현법

대부분 O(빅오)로 표현하고 있으므로, 시간복잡도 산출은 빅오를 사용하자.

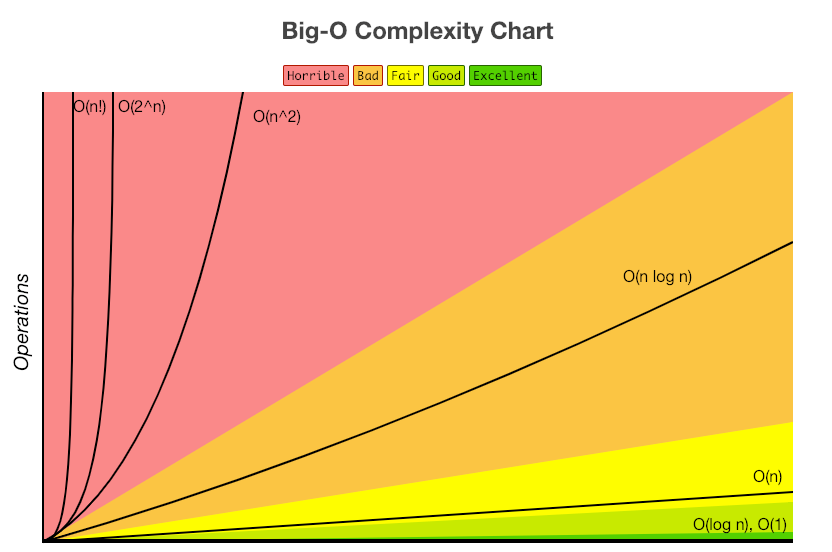
ExcellentO(1) Good O(log n) > FairO(n) > BadO(n log n) > Horrible > O(n^2) > O(2^n) > O(n!)

빅오 표기법 계산 방법(예시 코드)

function big_o(n){
  let sum =0; // 연산 1회 수행
  
  sum = n * 2; // 연산 1회 수행
  
  return sum; // 연산 1회 수행 
}

총 3회의 연산 코드 수행 -> 3 -> O(1) Excellent

function big_o(arr, n){
  let sum =0; // 연산 1회 수행
  
  for(let i = 0; i < n; i++){ // 연산 n회 수행(n의 값에 따라 달라짐)
  	sum += arr[i];
  }
 
  return sum; // 연산 1회 수행 
}

총 n+2회의 연산 코드 수행 -> n+2 -> 상수 날림 -> O(N) Fair 마지노선

function big_o(arr, n){
  let sum =0; // 연산 1회 수행
  
  for(let i = 0; i < n; i++){ // 연산 n*n 수행(n번 만큼 n번 수행) : n^2
	for(let j = 0; j < n; j++){
    	sum += arr[i][j];
    }   
  }
 
  return sum; // 연산 1회 수행 
}

총 n^2+2회의 연산 코드 수행 -> n^2+2 -> 상수 날림 -> O(N^2) Horrible n이 커질수록 많이 느림

function big_o(n){
  let sum =0; // 연산 1회 수행
  
  for(let i = 0; i < n; i *= 2){ // 연산 n/2회 수행
	sum += 2;
  }
 
  return sum; // 연산 1회 수행 
}

총 n/2+2회의 연산 코드 수행 -> n/2+2 -> 상수 날림 -> O(Log N) Good 나누기가 있으면 Log로 표시한다 병합정렬 분할정복

Data Structure Operations

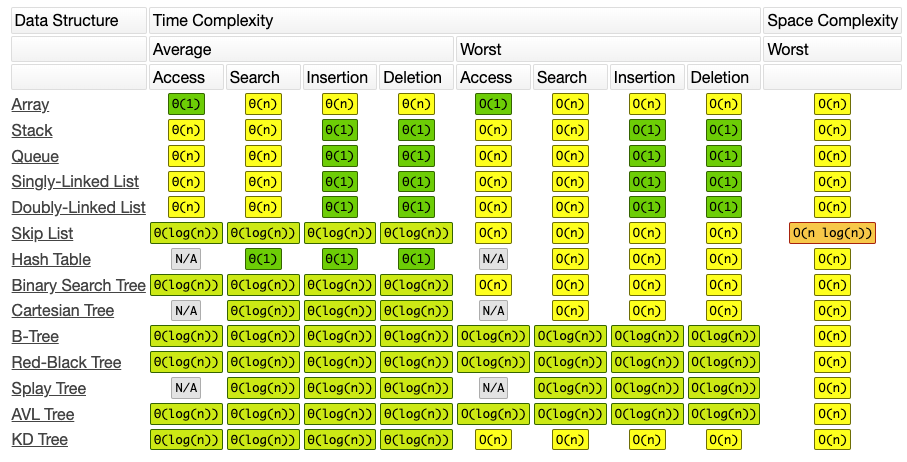
이미지 출처 : bigocheatsheet

Hash Table의 시간복잡도가 평균 O(1)으로 현업에서도 가장 많이 사용된다. (Red-Black / B-Tree도 많이 사용된다.)

Array Sorting Algorithms

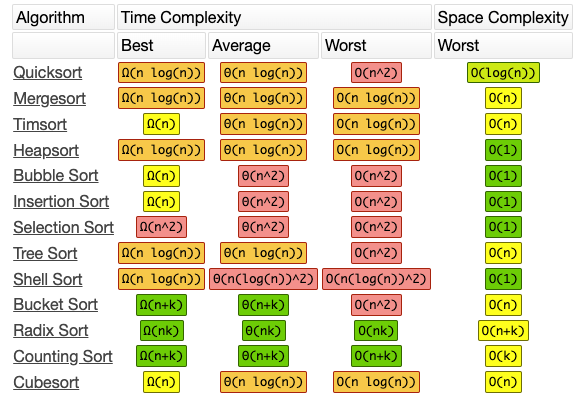
이미지 출처 : bigocheatsheet

정렬 알고리즘 별로 다른 시간복잡도가 나온다. 위 내용들을 잘 참고해서 알고리즘을 짜야한다.