Abstract

금융 포트폴리오 관리와 강화학습 기반 접근법

포트폴리오 관리란?

• 자금을 다양한 금융 상품에 지속적으로 재분배하는 과정을 의미합니다.

논문 핵심 아이디어:

• 모델 프리 금융 강화학습 프레임워크:
  • 전통적인 금융 모델 없이, 강화학습을 기반으로 한 딥러닝 솔루션을 제시합니다.
  • 금융 포트폴리오 관리 문제를 해결하기 위해 설계되었습니다.

주요 구성 요소:
1. EIIE (Ensemble of Identical Independent Evaluators) 토폴로지:

• 동일한 구조의 평가자들을 여러 개 구성하여, 다양한 관점에서 시장 상황을 평가합니다.

2. PVM (Portfolio-Vector Memory):
   • 포트폴리오의 상태를 효과적으로 저장 및 활용하여, 빠르고 정확한 의사결정을 지원합니다.
3. OSBL (Online Stochastic Batch Learning) 스킴:
   • 실시간으로 데이터를 학습하는 배치 방식으로, 시장의 변동성에 대응합니다.
4. 명시적인 보상 함수:
   • 에이전트가 금융 거래에서 얻은 결과에 따라 구체적인 보상을 주어, 최적의 전략을 학습하도록 유도합니다.

모델 구현:

• 세 가지 신경망 구조로 실현됨:
  • CNN: 이미지나 패턴 인식에 강점
  • RNN: 순차적인 데이터 처리에 효과적
  • LSTM: 장기 의존성 문제를 해결하여, 시계열 데이터 분석에 적합

실험 및 결과:

• 실험 환경:
  • 암호화폐 시장에서 30분 단위의 거래 데이터를 사용하여 백테스트 진행
• 성과:
  • 세 가지 모델 모두 다른 기존의 거래 알고리즘을 앞서며, 모든 실험에서 상위 3위를 기록
  • 높은 거래 수수료(0.25%) 조건에서도 50일 만에 최소 4배 이상의 수익률 달성

핵심 키워드:
Machine Learning, CNN, RNN, LSTM, Reinforcement Learning, Deep Learning, Cryptocurrency, Bitcoin, Algorithmic Trading, Portfolio Management, Quantitative Finance

---

Introduction

딥 포트폴리오 매니지먼트: 강화학습 기반 금융 포트폴리오 관리 시스템

배경 및 문제점
전통적인 포트폴리오 관리는 투자 자금을 다양한 금융 상품에 재분배하여 수익을 극대화하면서 위험을 최소화하는 과정입니다. 기존 방법들은 주로 사전에 구축된 금융 모델이나 단순 회귀 기반의 가격 예측에 의존하는데, 미래 가격 예측의 어려움과 추가적인 로직 계층 도입의 한계가 존재합니다.

제안하는 솔루션
본 논문에서는 미래 가격 예측 없이 순수한 강화학습(RL) 기반의 금융 포트폴리오 관리 프레임워크를 제안합니다. 주요 구성 요소는 다음과 같습니다:

• EIIE 토폴로지 (Ensemble of Identical Independent Evaluators):
  각 자산의 과거 가격 데이터를 입력받아, 단기 성장 가능성을 평가하는 독립 신경망들을 앙상블로 구성합니다. 평가 점수는 이전 포트폴리오 비중의 변화와 함께 고려되어, 새로운 포트폴리오 비중(즉, 시장 행동)을 결정하는 데 활용됩니다.

• PVM (Portfolio-Vector Memory):
  이전 거래 기간의 포트폴리오 상태를 저장하여, 거래 비용과 같은 요소를 반영할 수 있도록 합니다.

• OSBL (Online Stochastic Batch Learning) 스킴:
  실시간으로 시장 데이터를 반영하며, 백테스트 및 실제 거래 중에도 지속적으로 학습할 수 있는 배치 학습 방식입니다.

모델 구현 및 실험

• 세 가지 네트워크 구조(CNN, RNN, LSTM)를 각각 활용하여 EIIE를 구현하였으며, 이를 암호화폐(특히 Bitcoin 등) 시장에서 30분 단위의 거래 데이터를 대상으로 백테스트하였습니다.
• 실험 결과, 제안한 프레임워크가 기존의 포트폴리오 선택 알고리즘을 능가하며, 높은 거래 수수료 조건에서도 50일 만에 최소 4배 이상의 수익률을 달성하는 성과를 보였습니다.

의의 및 향후 연구

• 이 연구는 강화학습을 통한 모델 프리 금융 포트폴리오 관리 접근법을 제시하여, 전통적 가격 예측 방식의 한계를 극복할 수 있음을 입증합니다.
• 향후, 다양한 금융 시장(예: 주식, 채권 등)에서의 적용 가능성과 실시간 대응 능력, 그리고 안정적인 학습 기법 개선을 위한 추가 연구가 필요합니다.

---

Problem Definition

1. 포트폴리오 관리란?

• 투자 자본을 다양한 금융 자산에 지속적으로 재분배하여 수익을 극대화하고 위험을 줄이는 의사결정 과정입니다.
• 자동 거래 로봇의 경우, 주기적으로 투자 결정을 내리고 실행하게 됩니다.

2. 거래 기간 (Trading Period)

• 시간 기반 접근:
  • 시간은 동일한 길이의 기간 (T)로 나뉘며, 본 연구에서는 (T = 30)분으로 설정됩니다.
• 가격 포인트:
  • 각 거래 기간에는 시가, 최고가, 최저가, 종가 등 4가지 주요 가격이 존재합니다.
  • 연속 시장에서는 각 기간의 시가가 전 기간의 종가로 간주됩니다.
• 가정:
  • 백테스트에서는 각 기간 시작 시 자산을 시가에 매매할 수 있다고 가정합니다.

3. 수학적 공식화 (Mathematical Formalism)

• 가격 벡터:
  

• 특별한 자산:

  • 포트폴리오의 첫 번째 자산은 현금(본 논문에서는 Bitcoin으로 가정)으로, 모든 가격이 1로 고정됩니다.
  $v_{0,t} = v_{0,t}^{(hi)} = v_{0,t}^{(lo)} = 1, \quad \forall t.$

• 가격 비율 벡터:

  • 각 자산의 가격 변화 비율을 나타내는 벡터는 다음과 같이 정의됩니다.
  $\mathbf{y}_t := \frac{\mathbf{v}_t}{\mathbf{v}_{t-1}},$

  즉,

  $\mathbf{y}_t = \left( \frac{v_{1,t}}{v_{1,t-1}}, \frac{v_{2,t}}{v_{2,t-1}}, \dots, \frac{v_{m,t}}{v_{m,t-1}} \right)^\top.$

• 포트폴리오 가치와 수익률:
  

  $p_t = p_{t-1} \cdot \left( \mathbf{y}_t \cdot \mathbf{w}_{t-1} \right).$

  • 수익률은

    $\rho_t = \frac{p_t}{p_{t-1}} - 1,$

    그리고 로그 수익률은

    $r_t = \ln \frac{p_t}{p_{t-1}} = \ln \left( \mathbf{y}_t \cdot \mathbf{w}_{t-1} \right).$

4. 거래 비용 (Transaction Cost)

• 문제:

  • 실제 매매 시 거래 수수료 등으로 인해 포트폴리오 가치가 감소합니다.

• 모델링:

  • 거래 후 포트폴리오 비중은 다음과 같이 변화합니다.
  $\mathbf{w}'_t = \frac{\mathbf{y}_t \odot \mathbf{w}_{t-1}}{\mathbf{y}_t \cdot \mathbf{w}_{t-1}},$

  여기서 ( \odot )는 원소별 곱셈을 의미합니다.

• 재조정:
  • 거래 시 발생하는 매매 비용(판매, 구매 수수료)을 고려하여 최종 포트폴리오 가치 및 수익률을 재계산합니다.
• 계산:
  

5. 두 가지 가정 (Two Hypotheses)

• Zero Slippage:
  • 시장의 유동성이 충분하여, 주문 시 마지막 가격으로 매매가 즉시 이루어진다고 가정합니다.
• Zero Market Impact:
  • 거래 규모가 시장에 영향을 미치지 않을 만큼 작다고 가정합니다.

---

Data Treatments

1. Asset Pre-Selection (자산 사전 선택)

• 배경:
  • 본 연구에서는 Poloniex 거래소에서 약 80개의 암호화폐 거래쌍을 다루지만, 실제로는 거래 로봇이 한 기간 동안 처리할 수 있는 자산 수를 제한합니다.
• 자산 선택 기준:
  • 거래량 상위 11개의 비현금(non-cash) 자산을 선택합니다.
  • 현금 자산(여기서는 Bitcoin)이 포함되어 전체 포트폴리오 크기는 12로 결정됩니다.
• 선정 이유:
  • 거래량이 많다는 것은 시장 유동성이 높음을 의미하여, 거래 시 가정한 "Zero Slippage"와 "Zero Market Impact"에 부합합니다.
  • 또한, 과거 30일간의 거래량을 기준으로 하여 단기적인 급등락에 따른 왜곡(생존 편향)을 줄입니다.

---

2. Price Tensor (가격 텐서)

• 입력 데이터 구조:

  • 신경망의 입력은 (X_t)라는 3차원 텐서로, 크기는 ((f, n, m))입니다.
    • (f = 3): 특징 수 (종가, 최고가, 최저가)
    • (n = 50): 최근 50기간의 데이터 (약 1일 1시간)
    • (m): 사전 선택된 비현금 자산의 수 (여기서는 11개)

• 정규화:
  

  $V_t = \left[ \frac{v_{t-n+1}}{v_t}, \frac{v_{t-n+2}}{v_t}, \dots, \frac{v_{t-1}}{v_t} \right]$

• 활용:
  

---

3. Filling Missing Data (누락 데이터 처리)

• 문제:
  • 선택된 암호화폐 중 일부는 거래 이력이 부족하여 과거 데이터에 NAN (Not A Number) 값이 존재할 수 있습니다.
• 기존 접근:
  • 이전 연구에서는 0.01의 감쇠율을 적용한 하락 가격 시계열로 누락 데이터를 채웠으나, 이로 인해 네트워크가 특정 자산을 기억해버리는 문제가 발생했습니다.
• 제안하는 방법:
  • 이번 연구에서는 누락된 데이터 포인트를 "평탄한" (0 감쇠율) 가격 시계열로 대체합니다.
  • 이렇게 하면, 신경망이 과거 부정적 기록에 기반한 결정을 내리지 않도록 하여, 실제 상승 추세에도 올바른 판단을 내릴 수 있도록 합니다.
• 추가 고려사항:
  • 새로운 EIIE 구조를 통해 네트워크가 개별 자산의 정체성을 파악하지 못하게 하여, 오래된 부정적 기록에 의한 편향을 줄입니다.

---

Reinforcement Learning

금융 포트폴리오 관리 문제를 해결하기 위해, 본 논문에서는 결정적 정책 기울기(Deterministic Policy Gradient)를 기반으로 한 강화학습(RL) 프레임워크를 제시합니다. 이 섹션에서는 환경, 에이전트, 보상 함수, 그리고 정책 학습 방법을 구체적으로 설명합니다.

---

4.1 환경과 에이전트 (The Environment and the Agent)

• 환경 정의:
  금융 시장은 모든 거래 가능한 자산과 시장 참가자들의 기대를 포함하는 복잡한 시스템입니다.
  

• 에이전트 역할:
  

• 상태와 행동의 연결:
  

---

4.2 전면 활용과 보상 함수 (Full-Exploitation and the Reward Function)

• 목표:
  

• 보상 함수 정의:

  • 평균 로그 누적 수익은 다음과 같이 정의됩니다.

    $R(s_1, a_1, \dots, s_{t_f}, a_{t_f}, s_{t_f+1}) := \frac{1}{t_f} \sum_{t=1}^{t_f} r_t,$

    여기서 ( r_t )는 t번째 기간의 로그 수익률이며,

    $r_t = \ln \left( \mu_t \, \mathbf{y}_t \cdot \mathbf{w}_{t-1} \right).$

• 특징:

  • 정확한 보상 표현: 모든 에피소드의 보상이 정확하게 표현되어, 동일한 데이터 구간에서 여러 행동 시퀀스를 평가할 수 있습니다.
  • 동일 가중치: 각 에피소드의 보상이 최종 수익에 동일하게 기여하므로, 할인율 없이 현재 행동의 가치 함수로 활용할 수 있습니다.
  • 이로 인해, 추가적인 탐색 없이도 전면 활용(full exploitation) 전략을 적용할 수 있습니다.

---

4.3 결정적 정책 기울기 (Deterministic Policy Gradient)

• 정책 정의:
  

• 목표 함수:
  

• 파라미터 업데이트:
  

---

결론

---

Policy Networks

5.1 Network Topologies (네트워크 토폴로지)

• EIIE 구조 (Ensemble of Identical Independent Evaluators):

  • 각 자산마다 동일한 구조(미니 머신)를 적용하여 개별 자산의 가격 이력을 평가합니다.
  • 네트워크의 파라미터는 모든 자산에 대해 공유되며, 마지막에 softmax를 통해 각 자산의 투자 비중을 산출합니다.
  • CNN 버전은 1×1 커널의 컨볼루션 체인으로 구성되며, RNN/LSTM 버전은 개별 자산의 시계열 데이터를 처리합니다.

• 장점:

  • Scalability: 동일한 네트워크 구조를 자산 수에 맞게 확장할 수 있어, 전체 자산 수가 늘어나도 효율적입니다.
  • Data Efficiency: 각 미니 머신이 여러 자산에 대해 동시에 학습되어, 경험이 시간과 자산 차원에서 공유됩니다.
  • Plasticity: 개별 자산의 정체성에 의존하지 않고, 새로운 자산이 추가되거나 포트폴리오 크기가 변해도 유연하게 대응할 수 있습니다.

---

5.2 Portfolio-Vector Memory (포트폴리오 벡터 메모리)

• 목적:
  
• 구현:
  • 경험 재현(Experience Replay)에서 영감을 받아, PVM은 시간 순서대로 포트폴리오 벡터를 저장하는 스택 구조로 구성됩니다.
  • 각 학습 단계에서, 정책 네트워크는 (t-1) 시점의 포트폴리오 벡터를 읽어와 현재의 결정을 내리고, 새로운 포트폴리오 벡터로 메모리를 업데이트합니다.
• 장점:
  • 미니 배치 학습 시, 동일한 메모리 스택을 공유함으로써 훈련 효율이 크게 향상됩니다.
  • 이전 결과에 의존하지 않고, 정규화된 가격 데이터와 함께 안정적인 거래 결정을 내릴 수 있도록 지원합니다.

---

5.3 Online Stochastic Batch Learning (온라인 확률적 배치 학습)

• 문제:
  • 금융 시장은 연속적인 시계열 데이터로 구성되며, 데이터 포인트 간의 순서가 중요합니다.
• 해결:
  • 미니 배치 학습 시, 시간 순서대로 데이터를 구성하여, 서로 겹치는 배치도 유효한 데이터 샘플로 활용합니다.
  • 새로운 데이터가 지속적으로 유입되는 환경(온라인 트레이딩)에 적합하도록, 각 거래 종료 후 최근 데이터로부터 랜덤하게 미니 배치를 선택하여 네트워크를 업데이트합니다.
• 특징:
  • 시간 순서 유지: 배치 내 데이터는 시간 순서대로 구성되어, 시계열 특성을 보존합니다.
  • 효율성: 새로운 데이터가 계속 추가되는 환경에서, 배치 학습으로 전체 데이터를 다시 처리하지 않고도 온라인 학습이 가능합니다.

---

---

Experiments

본 섹션에서는 제안된 포트폴리오 관리 강화학습 프레임워크(특히 EIIE 기반 정책 네트워크)를 암호화폐 거래소 Poloniex에서 백테스트 실험을 통해 평가한 내용을 소개합니다.

---

1. 실험 환경 및 데이터 범위

• 테스트 범위:

  • 여러 시간대(예: Back-Test1, Back-Test2, Back-Test3)에서 실험을 진행하였으며, 각 실험의 데이터 범위와 학습 세트는 Table 1에 정리되어 있습니다.
  • 모든 가격 데이터는 30분 간격으로 수집되었고, 백테스트와 하이퍼파라미터 선택에는 UTC 기준 데이터가 사용되었습니다.

• 데이터 처리:

  • 자산 사전 선택, 가격 텐서 구성, 그리고 데이터 정규화 등의 전처리 과정을 통해 시장 상태를 효과적으로 표현하였습니다.

---

2. 평가 지표 (Performance Measures)

• 누적 포트폴리오 가치 (APV):
  

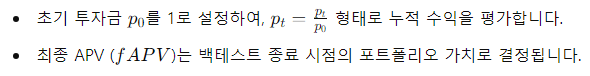
• Sharpe Ratio (SR):
  

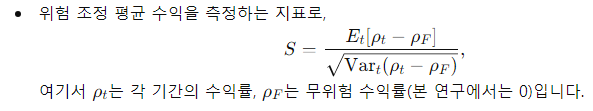
• Maximum Drawdown (MDD):
  • 포트폴리오 가치의 최대 하락폭을 나타내며,
    $D = \max_{t > \tau} \frac{p_t - p_{\tau}}{p_t},$
    즉, 최고점에서 최저점까지의 손실 비율로 계산됩니다.

---

3. 실험 결과 요약

• EIIE 네트워크 성능:

  • 제안된 CNN, bRNN, LSTM 기반 EIIE 네트워크는 fAPV와 SR 측면에서 모든 백테스트에서 경쟁 전략들을 크게 능가했습니다.
  • 특히, EIIE 네트워크는 거래 비용(0.25% 수수료)와 30분 간격의 높은 거래 빈도 조건에서도 20일 내에 최소 4배 이상의 수익을 달성했습니다.

• 비교 대상:

  • 벤치마크: Best Stock (시장 최고 성과 자산), UCRP (동일 비중 유지), UBAH (동일 구매 후 보유) 등이 포함되었습니다.
  • 기존 모델 기반 전략: RMR, OLMAR, PAMR, CWMR 등과 비교하여, 전통적 모델 기반 전략들은 Back-Test1에서 대부분 음의 수익률을 보였으나, EIIE 네트워크는 안정적으로 시장을 능가하는 성과를 나타냈습니다.

• 시각화:

  • Figures 5, 6, 7에서는 각 백테스트 기간 동안 APV가 시간에 따라 어떻게 변화했는지 플롯으로 제시되며, CNN과 bRNN 기반 EIIE가 지속적으로 시장을 이겼음을 보여줍니다.

---

결론

실험 결과, 제안된 EIIE 기반 정책 네트워크는 기존의 모델 기반 전략과 벤치마크를 모두 능가하는 성과를 보였습니다.

• 주요 성과:
  • fAPV와 Sharpe Ratio에서 탁월한 성능을 보이며, 시장의 다양한 상황에서도 안정적인 수익을 기록했습니다.
  • 특히, 거래 비용과 높은 거래 빈도 조건에서도 강력한 수익률을 유지함으로써, 자동 포트폴리오 관리의 실용성을 입증했습니다.

이러한 결과는 강화학습 기반 금융 에이전트가 실제 시장에서도 경쟁력 있는 투자 전략을 구현할 수 있음을 시사하며, 향후 추가적인 연구와 확장이 기대됩니다.

Conclusion

본 논문은 금융 포트폴리오 관리 문제를 해결하기 위한 확장 가능한 강화학습 프레임워크를 제안했습니다. 주요 내용은 다음과 같습니다.

• EIIE 메타 토폴로지:

  • 여러 개의 미니 머신(Identical Independent Evaluators)을 통해 각 자산을 독립적으로 평가하고, softmax를 통해 포트폴리오 비중을 결정합니다.
  • 이러한 구조 덕분에 에이전트는 자산 수에 대해 선형적으로 확장 가능하며, 데이터 효율성과 유연성이 크게 향상됩니다.

• Portfolio-Vector Memory (PVM):

  • 이전 거래의 포트폴리오 벡터를 저장하여, 거래 비용을 최소화하고 과도한 자산 변경을 방지합니다.
  • 병렬 학습을 가능하게 하여, RNN 기반 방식보다 효율적으로 학습할 수 있습니다.

• Online Stochastic Batch Learning (OSBL):

  • 실시간으로 들어오는 시장 데이터를 미니 배치 단위로 학습하여, 온라인 학습에 적합한 환경을 구축합니다.

• 학습 방법 및 보상 함수:

  • 결정적 정책 기울기(Deterministic Policy Gradient)를 활용하여, 누적 수익(평균 로그 수익)을 극대화하는 방향으로 파라미터를 업데이트합니다.
  • 전체 강화학습 구조는 명확한 보상 함수와 함께, 모든 에피소드의 보상이 동등하게 반영되도록 설계되었습니다.

• 실험 결과:

  • 제안한 CNN, 기본 RNN, LSTM 기반 EIIE 네트워크 모두 백테스트에서 전통적인 포트폴리오 선택 전략들을 능가하는 성과를 보였습니다.
  • 특히, EIIE 네트워크들은 최종 누적 포트폴리오 가치(fAPV)와 위험조정 수익(SR)에서 우수한 성능을 기록하며, 시장 상황에 안정적으로 대응함을 입증했습니다.
  • 다만, LSTM 네트워크는 기억 능력이 지나치게 오래된 정보를 유지하여 성능 차이가 발생할 수 있음이 관찰되었습니다.

• 향후 연구 방향:

  • 시장 영향과 슬리피지: 현재의 “zero market impact”와 “zero slippage” 가정을 극복하기 위해, 실제 거래 데이터를 기반으로 한 추가 학습이 필요합니다.
  • 다양한 시장 환경 테스트: 암호화폐 시장 외에도 전통 금융 시장 등 다른 환경에서의 성능 평가가 요구됩니다.
  • 보상 함수 개선: 장기적인 시장 반응까지 반영하는 보상 함수(예: Critic 네트워크 도입)로 확장할 수 있는 방안을 모색해야 합니다.