재귀 함수 연습하기 3

재귀 함수 연습하기 마지막 시간입니다! 🥳🥳🥳 마지막 시간인만큼 이제까지 만났던 문제들보다 조금 더 복잡한 문제를 가져와 봤는데요.

하노이의 탑은 1883년 프랑스 수학자 루카스로부터 고안된 문제로서 수학 뿐만 아니라 컴퓨터 이론에서도 자주 활용되는 예제입니다.

이제 이 하노이의 탑을 하나의 재귀 함수로 작성해볼 겁니다.

🛕 하노이의 탑

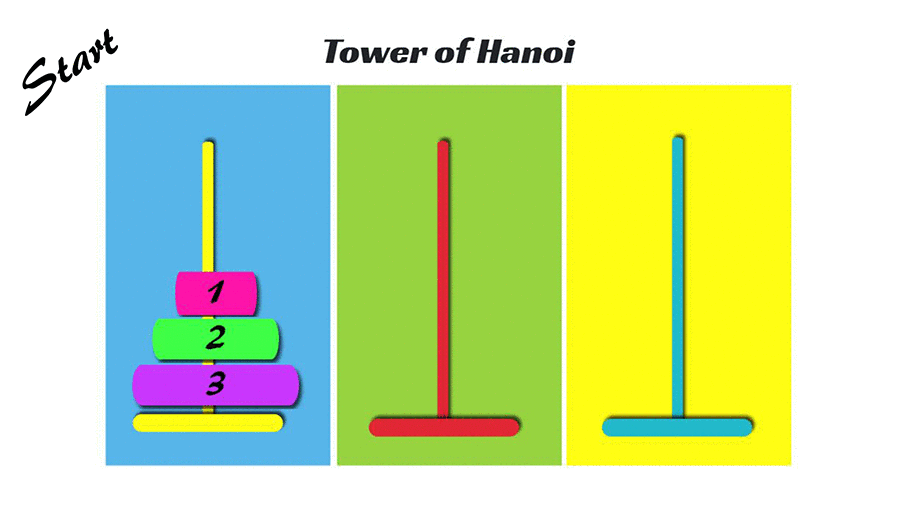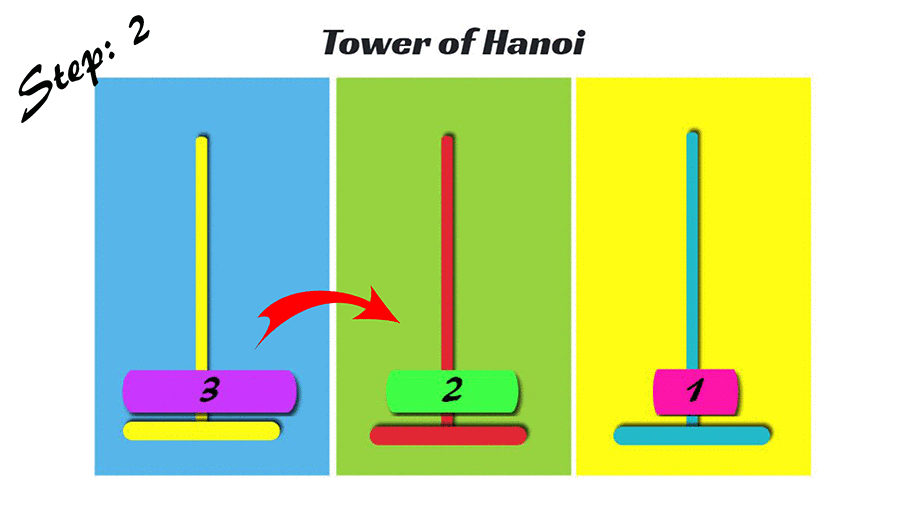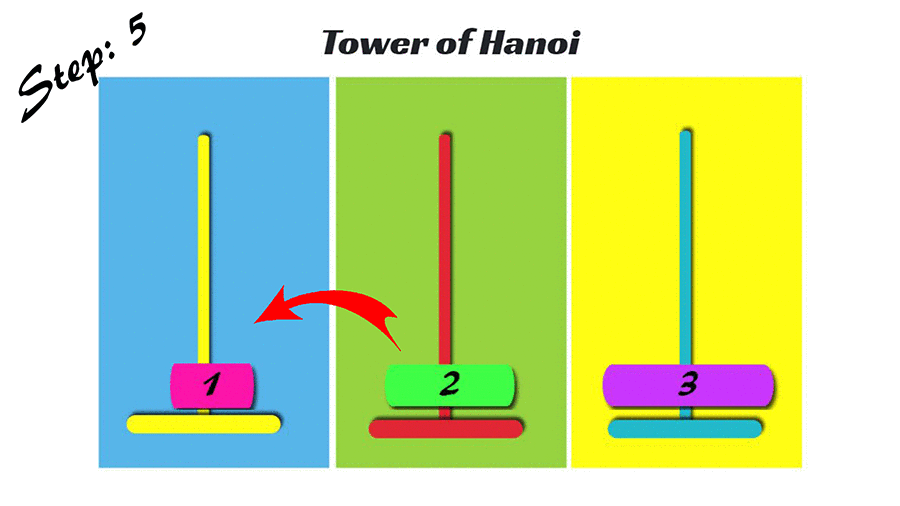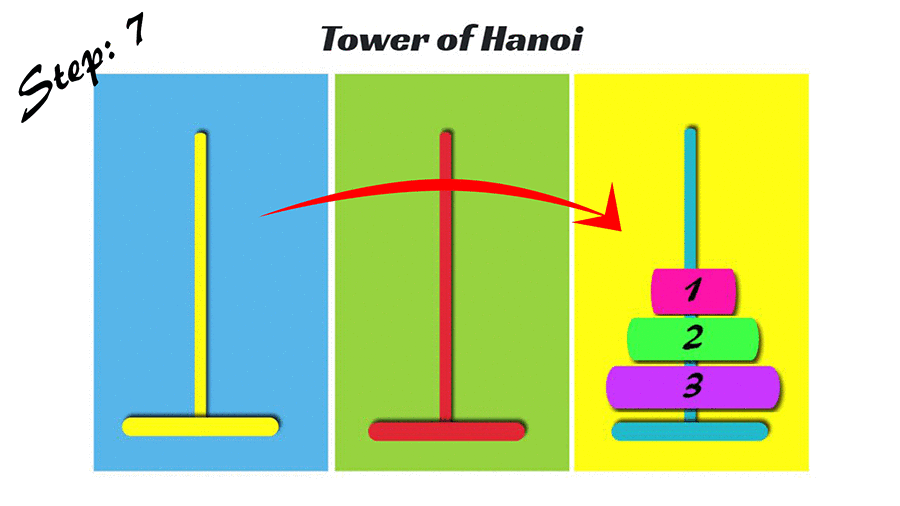
우리의 목표는 왼쪽 기둥에 있는 원판들을 모두 오른쪽 기둥으로 옮기는 것입니다. 아래의 두 가지 규칙과 함께 말이죠.

1. 한 번에 하나의 원판만 옮기기
2. 큰 원판이 작은 원판 위에 있으면 안 됨!

우리가 작성할 함수 hanoi는 하노이의 탑 게임의 해답을 출력해줍니다. 이 함수는 파라미터로 원판 수 num_disks와 시작 기둥 번호인 start_peg, 그리고 목표 기둥 번호인 end_peg를 받습니다.

hanoi는 재귀 함수입니다. 따라서, 재귀적으로 문제를 풀어 원판을 옮기는 순서를 모두 출력해야 합니다. 답안의 예제를 보여드리겠습니다.

1. 원판이 하나인 경우

hanoi(1, 1, 3)

1번 원판을 1번 기둥에서 3번 기둥으로 이동

2. 원판이 두 개인 경우

hanoi(2, 1, 3)

1번 원판을 1번 기둥에서 2번 기둥으로 이동
2번 원판을 1번 기둥에서 3번 기둥으로 이동
1번 원판을 2번 기둥에서 3번 기둥으로 이동

3. 원판이 세 개인 경우

hanoi(3, 1, 3)

1번 원판을 1번 기둥에서 3번 기둥으로 이동
2번 원판을 1번 기둥에서 2번 기둥으로 이동
1번 원판을 3번 기둥에서 2번 기둥으로 이동
3번 원판을 1번 기둥에서 3번 기둥으로 이동
1번 원판을 2번 기둥에서 1번 기둥으로 이동
2번 원판을 2번 기둥에서 3번 기둥으로 이동
1번 원판을 1번 기둥에서 3번 기둥으로 이동

함수 작성 전, 원판을 옮겨주는 move_disk 함수부터 정의하겠습니다. 이 함수는 hanoi 함수에 의해 출력될 게임의 순서를 담아야 합니다.

def move_disk(disk_num, start_peg, end_peg):
    print(f"{disk_num}번 원판을 {start_peg}번 기둥에서 {end_peg}번 기둥으로 이동")

이제 hanoi의 base case와 recursive case를 구해봅시다.

먼저 base case부터 볼까요? 언제 우리는 hanoi의 정답을 가장 쉽게 구할 수 있을까요? 바로 원판이 하나도 없을 때입니다. 원판이 하나도 없다면 게임이 자동으로 종료되기 때문이죠. 이를 코드로 구현해 봅시다.

def hanoi(num_disks, start_peg, end_peg):
    if num_disks == 0:
        return

다음으로 원판의 수에 따른 몇 가지 예시를 보며 recursive case를 구해봅시다.

원판이 하나일 때부터 생각해볼까요? 원판이 하나면, 시작 기둥에 있는 원판을 끝 기둥으로 옮기기만 하면 됩니다.

원판이 두 개일 때는 어떨까요? 맨 위에 있는 작은 원판을 목표 기둥에 옮기고 그 다음 큰 원판을 그 위에 올리면 되나요? 정답은 땡입니다! ❌❌❌

하노이의 탑 게임 규칙을 기억하시나요? 큰 원판은 작은 원판 위에 있어서는 안됩니다. 그렇다면 기둥은 단 두 개뿐인데 규칙을 지키면서 어떻게 옮길 수 있을까요?

기둥이 두 개일 때는 무슨 수를 써도 규칙대로 원판을 옮길 수 없습니다. 따라서, 원판이 두 개일 때부터는 시작 기둥과 끝 기둥 뿐만 아니라 새로운 기둥이 하나 더 필요합니다. 큰 원판이 머무를 임시 거처가 필요한 것이죠. 이 임시 기둥을 middle_peg라고 합시다.

이제 3개의 기둥이 생겼습니다. 첫 단계에서 시작 번호에 있는 작은 원판은 middle_peg로 옮겨집니다. 그래야 남아 있는 큰 원판이 먼저 목표 원판에 놓일 수 있게 되니까요. 그 다음 마지막으로 middle_peg에 있는 작은 원판을 큰 원판 위에 올려 놓으면 됩니다.

여기까지 총 세 개의 단계가 필요했습니다. 따라서, 원판이 두 개일 때의 순서도 세 줄이 나오는 것이구요.

마지막으로 원판이 세 개일 때를 봅시다. 원판이 세 개가 되면 조금 더 복잡해집니다. 따라서, 순서를 메뉴화해서 보여드리겠습니다.

1. 가장 작은 원판을 시작 기둥에서 목표 기둥으로 옮긴다
2. 중간 원판을 시작 기둥에서 임시 기둥으로 옮긴다
3. 가장 작은 원판을 목표 기둥에서 임시 기둥으로 옮긴다
4. 가장 큰 원판을 시작 기둥에서 목표 기둥으로 옮긴다
5. 가장 작은 원판을 임시 기둥에서 시작 기둥으로 옮긴다
6. 중간 원판을 임시 기둥에서 목표 기둥으로 옮긴다
7. 가장 작은 원판을 시작 기둥에서 목표 기둥으로 옮긴다

지금까지 원판이 하나일 때, 둘일 때, 셋일 때의 사례를 봤습니다. 이를 자세히 들여다보면 공통점이 보이는데요.

마지막 원판이 시작 기둥으로부터 목표 기둥으로 옮겨지면 임시 기둥에 있던 나머지 원판들이 마지막으로 목표 기둥에 옮겨진다는 것이죠. 이는 원판이 네 개인 경우에도 마찬가지입니다.

따라서 hanoi의 부분 문제는 마지막 원판과 나머지 원판들의 이동으로 정의내릴 수 있습니다. 이를 매뉴얼로 정리하면 다음과 같습니다.

1. 가장 큰 원판을 제외한 나머지 원판들을 start_peg에서 middle_peg로 옮김
2. 가장 큰 원판을 start_peg에서 end_peg로 옮김
3. 나머지 원판들을 middle_peg에서 end_peg로 옮김

hanoi를 코드로 구현하기에 앞서, 해야될 일이 한 가지 더 있습니다. 바로 임시 기둥 middle_peg를 정의하는 것이죠.

start_peg와 end_peg를 각각 1번 기둥, 3번 기둥이라 칭한다면 middle_peg는 이들의 중간 값인 2번 기둥이 됩니다. 이 때, 세 수를 더하면 1 + 2 + 3 = 6이 되므로 middle_peg는 다음과 같이 정의할 수도 있습니다.

middle_peg = 6 - start_peg - end_peg

이렇게 정의하는 이유는 목표 기둥에서 시작 기둥으로 옮기는 과정에서 음수가 나오는 것을 방지하기 위함입니다. 아래 작성될 코드를 보면 이를 이해하기 더 쉬울 것입니다.

이제 코드를 차례로 한 줄씩 작성해봅시다.

앞서 원판이 하나도 없을 때를 base case로 두고 작성했었죠? 만약 원판이 하나라도 있다면 게임은 종료되지 않고 이어져야 합니다.

원판이 두 개일 때부터 임시 기둥이 필요했습니다. 따라서, 임시 기둥부터 정의를 하고 recursive case를 구현하면 됩니다.

임시 기둥에 대한 정의는 이미 했으니 바로 recursive case에 대한 코드를 작성해봅시다.

가장 먼저 필요한 것은 가장 큰 원판을 제외하고 나머지 원판들이 시작 기둥으로부터 임시 기둥으로 옮겨지는 과정에 대한 코드입니다.

hanoi(num_disks - 1, start_peg, middle_peg)

예를 들어 원판이 세 개일 경우, hanoi의 첫 파라미터로 3이라는 숫자가 입력됩니다. 따라서, 나머지 원판들의 수는 3에서 1을 뺀 2가 되는 것이죠. 이는 base case인 num_disks가 0이 되기 전까지 계속 실행됩니다.

다음으로 가장 큰 원판을 시작 기둥에서 목표 기둥으로 옮겨야 합니다. 이 과정은 move_disk 함수를 통해 화면에 출력되어야 합니다.

move_disk(num_disks, start_peg, end_peg)

마지막으로 나머지 원판들을 임시 기둥에서 목표 기둥으로 옮겨야 합니다.

hanoi(num_disks - 1, middle_peg, end_peg)

이 또한 num_disks가 base case에 도달하기 전까지 반복적으로 실행됩니다.

이제 완성된 전체 코드를 봅시다.

def move_disk(disk_num, start_peg, end_peg):
    print(f"{disk_num}번 원판을 {start_peg}번 기둥에서 {end_peg}번 기둥으로 이동")

def hanoi(num_disks, start_peg, end_peg):
    if num_disks == 0:
        return
    
    else:
        middle_peg = 6 - start_peg - end_peg
        
        hanoi(num_disks - 1, start_peg, middle_peg)
        move_disk(num_disks, start_peg, end_peg)
        hanoi(num_disks - 1, middle_peg, end_peg)

결국 가장 큰 원판을 제외하고 나머지 원판들에 대해서는 재귀 함수를 적용하여 base case에 도달하기 전까지 계속해서 호출이 이루어집니다.

아직도 이해가 어려우신 분들을 위해 예시를 통해 더 자세히 알아보도록 하겠습니다.

hanoi(3, 1, 3)이 실행하는 코드를 보면 각각 hanoi(2, 1, 2) / move_disk(3, 1, 3) / hanoi(2, 2, 3)이 있는데요.

여기서 hanoi(2, 1, 2)는 다시 hanoi(1, 1, 3)을 호출한 후에 move_disk(2, 1, 2), hanoi(1, 3, 2)를 실행하게 됩니다.

따라서, hanoi(1, 1, 3)이 가장 먼저 출력되고(이 이후로는 base case가 되므로) 뒤이어 move_disk(2, 1, 2), hanoi(1, 3, 2)가 순차적으로 실행됩니다.

첫 줄의 재귀가 끝나고서야 처음에 호출한 hanoi(3, 1, 3)의 다음 줄인 move_disk(3, 1, 3)이 실행됩니다. 여기서는 재귀가 없기 때문에 실행된 후에는 바로 다음 줄로 넘어가 hanoi(2, 2, 3)을 실행합니다.

hanoi(2, 2, 3)은 첫 줄인 hanoi(3, 1, 3)과 마찬가지로 middle_index를 재조정한 후, 다시 순차적으로 진행됩니다.

정리하자면 hanoi는 재귀적으로 호출되면서 base case에 도달하기 전까지 바뀐 값을 실행하게 되고 가장 마지막에 도달한 값만을 move_disk를 통해 출력합니다.

❗ 시간 복잡도

우선 재귀 부분을 제외하면 hanoi의 시간 복잡도는 O(1)입니다.

이제 hanoi 함수가 호출되는 총 횟수를 알면 됩니다. recursive case에서 원판 수 num_disks를 n이라고 할 때, hanoi는 'n - 1' 크기의 부분 문제 2개를 계속해서 만들어냅니다.

다시 말해, hanoi 함수는 n이 0이 되기 전까지 계속해서 재귀적으로 더 작은 hanoi를 호출하고 그때마다 부분 문제 2개를 계속해서 만들어내는데, 이는 곧 hanoi 함수가 호출될 때마다 n번만큼 부분 문제가 2배로 늘어나는 것을 의미합니다.

따라서, hanoi의 총 시간 복잡도는 O(2^n)이 됩니다.

---

지금까지 하노이의 탑 사례를 통해 재귀 함수 구현 방법을 알아보았습니다. 많이 어려우셨나요? 하지만 여기까지 잘 따라왔다는 것은 앞으로의 알고리즘 문제에 더 쉽게 다가갈 수 있음을 의미합니다.

거대한 문제 하나를 해결하기 위해 부분 문제를 나누는 것이 알고리즘의 핵심입니다. base case와 recursive case를 항상 염두에 두고 문제를 풀어봅시다.

다음 시간부터는 알고리즘 문제를 해결하기 위한 여러 접근법인 알고리즘 패러다임에 대해 함께 알아보겠습니다. 지금까지 수고 많으셨습니다! 🥳🥳🥳

* 이 자료는 CODEIT의 '알고리즘의 정석' 강의를 기반으로 작성되었습니다.