지난 시간에는 나누고 정복하고 합치는 Divide and Conquer 알고리즘 패러다임에 대해 배웠습니다.
이번 시간에는 새로운 알고리즘 패러다임 Dynamic Programming에 대해 함께 알아봅시다 :)
💃 최적 부분 구조
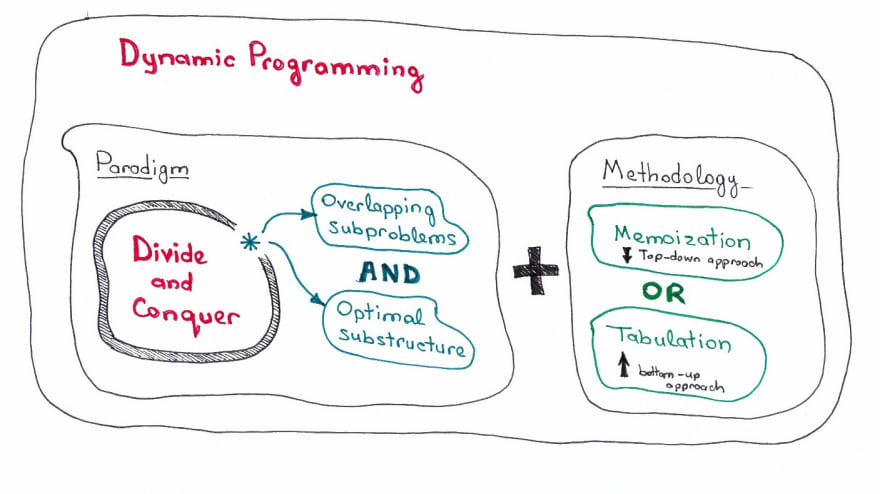
Dynamic Programming에 대해 배우기에 앞서 Dynamic Programming에 필요한 두 조건을 알려드리겠습니다.
- 최적 부분 구조(Optimal Substructure)
- 중복되는 부분 문제(Overlapping Subproblems)
먼저 첫 번째 조건인 최적 부분 구조에 대해 알아봅시다. 최적 부분 구조가 있다는 것은 부분 문제들의 최적의 답을 이용해서 기존 문제의 최적의 답을 구할 수 있다는 것을 의미합니다.
예시를 한 번 볼까요? 피보나치 수열 기억하시나요? 다섯 번째 피보나치 수열을 구하기 위해서는 네 번째 피보나치 수열과 세 번째 피보나치 수열을 구해야 합니다.
이 두 부분 문제의 최적의 답을 구하면 기존 문제의 최적의 답을 구할 수 있죠. 세 번째 피보나치 수와 네 번째 피보나치 수의 합이 다섯 번째 피보나치 수가 되니까요.
따라서, 피보나치 수열은 최적 부분 구조를 갖고 있는 문제라고 할 수 있습니다.
💃 중복되는 부분 문제
우리는 재귀 함수부터 부분 문제에 대한 개념을 여러 차례 접했습니다.
앞서 fib(5)를 구하기 위해 fib(4)와 fib(3)이라는 부분 문제를 해결해야 한다고 했습니다. 그런데 fib(4)를 해결하기 위해서는 또, fib(3)과 fib(2)라는 부분 문제를 해결해야 하는데요. 마찬가지로 fib(3)을 해결하기 위해서는 fib(2)와 fib(1)을 해결해야 합니다. fib(2)와 fib(1)은 base case므로 그냥 두면 됩니다.
fib(4)의 문제를 해결했으니 이제 나머지 fib(3)의 문제를 따로 해결해야 하는데요. 이렇게 하다보면 중복되는 부분 문제들이 있습니다. fib(3)을 두 번 계산하게 되죠?
fib(7)이라면 어떨까요? 이를 계산하는 과정에서 fib(5)도 중복으로 계산하고 fib(4)도 여러번 계산하며 fib(3)도 여러번 계산합니다. 이와 같은 계산을 중복되는 부분 문제라고 합니다.
주의할 것은 문제를 부분으로 나눈다고 항상 중복되는 문제가 있는 것은 아니라는 점입니다. 예를 들어, Divide and Conquer를 사용하는 합병 정렬을 봅시다.
8개의 요소가 담긴 리스트를 정렬하기 위해서는 4개의 요소가 담긴 리스트 두 개로 나누고 이 둘을 각각 합병 정렬해야겠죠?
그런데 왼쪽 반을 해결하는 과정과 오른쪽 반을 해결하는 과정은 완전히 독립적입니다. 서로 중복되는 부분이 없다는 것이죠. 그렇기 때문에 합병 정렬의 두 부분 문제는 중복되지 않는 부분 문제(Non-overlapping Subproblem)입니다.
💃 Dynamic Programming
앞서 최적 부분 구조가 있다는 것이 부분 문제의 최적의 답을 이용해서 기존 문제를 풀 수 있다는 것을 의미한다고 했습니다. 이는 다시 말하면 기존 문제를 부분 문제로 나눠서 풀 수 있다는 것을 뜻합니다.
그런데 이렇게 부분 문제로 나눠서 풀다보면 중복되는 부분 문제들이 있을 수 있습니다. 그럼 똑같은 문제를 여러번 풀어야 하는 비효율이 생기기도 합니다. 이런 비효율을 해결하는 방법이 바로 Dynamic Programming입니다.
Dynamic Programming을 간단히 설명하자면 한 번 계산한 결과를 버리지 않고 재활용하는 방식이라고 할 수 있습니다. 중복되는 문제를 다시 푸는 게 아니라 한 번만 풀고 기억해 두는 것이죠.
fib(7)을 예로 들면 반복되는 fib(4)와 fib(3)과 같은 문제를 여러번 풀지말고 딱 한 번만 풀자는 것이 Dynamic Programming의 취지입니다.
이를 구현하는 방법은 또 두 가지로 나뉘는데요. 첫 번째는 Memoization, 두 번째는 Tabulation입니다.
💃 Memoization
분식집에서 떡볶이를 먹으면 순대와 오뎅을 같이 먹는 고객들이 있습니다. 이러한 경우가 많다보니 일일히 떡복이, 순대, 오뎅을 따로 계산하는 것이 번거롭게 느껴지는데요. 따라서, 이들을 세 개로 묶어 세트로 팔기로 하니 계산이 수월해졌습니다.
이렇게 중복되는 계산이 있으면 한 번만 계산하고 메모를 한 뒤 이후에는 메모를 참고하기만 하면 되는데요. 이런 방식을 Memoization이라고 부릅니다. 그럼 프로그래밍에서는 Memoization을 어떻게 구현할 수 있을까요?
다시 피보나치 수로 예를 들어봅시다. 피보나치 수를 계산하기 전에 사전을 하나 만든다고 가정하겠습니다. 이 사전에는 한 번 계산한 값을 저장해 둘 건데요. 보통 이렇게 다시 사용할 값들을 저장해 놓는 공간을 '캐시(Cache)'라고 부릅니다.
이제 다섯 번째 피보나치 수를 구하는 문제가 있다고 합시다. fib(5)는 fib(4)와 fib(3)이라는 부분 문제를 해결하면 구할 수 있습니다. 그런데 fib(4)는 다시 fib(3)과 fib(2)로 fib(3)은 fib(2)와 fib(1)이라는 부분 문제로 나뉩니다.
fib(2)와 fib(1)은 base case죠? 따라서 둘 다 1이라는 값을 가집니다. 그런데 이 둘은 언젠가 다시 쓰일 수도 있기 때문에 아까 만들어준 캐시 사전에 넣어줍니다.
이제 이 두 값을 알았으니 fib(3)도 구할 수 있겠죠? fib(2)와 fib(1)을 더하면 되니까요. fib(3)의 결과는 2가 나오고 이 값도 캐시 사전에 넣어줍니다. fib(4)를 해결하기 위한 두 부분 문제에서 fib(3)은 구했고 나머지 fib(2)는 캐시 사전에서 값을 가져다 씁니다. 그럼 fib(4)의 값을 구했죠?
fib(4)의 반대편 fib(3)은 캐시로부터 값을 가져다 쓰면 됩니다. 그럼 fib(4)와 fib(3)을 모두 구했으니 기존 문제인 fib(5)를 구할 수 있습니다.
자, 여기까지 중복되는 문제는 모두 캐시 사전에서 꺼내 쓰고 처음 푸는 문제들만 딱 한 번 풀었죠? 이것이 바로 Memoization에 의한 Dynamic Programming으로 중복되는 부분 문제의 비효율성을 해결하는 방법입니다.
❗ Memoization 구현하기
Memoization을 실제 코드로 접해봅시다. 앞서 설명한 피보나치 수열 구하는 문제를 활용하겠습니다.
fib_memo는 n번째 피보나치 수를 찾아주는 함수입니다. Memoization 방식을 활용하기 위해서는 반복되는 연산을 저장할 공간이 필요하다고 했죠? 따라서 fib이라는 함수를 통해 n번째 피보나치 수를 담을 사전을 만들어 주겠습니다.
def fib(n):
fib_cache = {}
return fib_memo(n, fib_cache)이 사전이 쓰이기 위해서는 피보나치 연산을 수행할 함수를 작성해야 합니다. 이 함수가 바로 우리가 작성하고자 하는 fib_memo입니다.
fib_memo의 파라미터는 정수 n과 사전 cache입니다. Memoization 방식으로 문제를 풀면 재귀 함수가 필요한데요. 따라서, base case와 recursive case를 찾아야 합니다.
피보나치 수열의 base case를 기억하시나요? n이 1과 2인 경우에는 1이라는 값을 갖는다는 것이 피보나치 수열의 조건입니다. 그리고 이 조건이 바로 피보나치 수열의 base case입니다.
if n < 3:
return 1이제 recursive case를 작성해야 하는데요. recursive case에는 두 가지 경우가 있습니다. 하나는 이미 n번째 피보나치 수를 계산한 경우이고 다른 하나는 아직 계산하지 않은 경우입니다.
전자는 cache[n] 즉, cache 사전의 key인 n에 대한 값이 존재하는 경우이고 후자는 n에 대한 값이 존재하지 않는 경우입니다.
key가 이미 존재하는 경우에는 해당 key값을 반환해주면 됩니다. 그러나 존재하지 않는 경우에는 피보나치 수열을 계산해야겠죠?
지난 시간에 사전의 개념을 배우며 사전 안에 특정 키가 있는지 확인하는 방법에 대해 배웠습니다. 바로 in과 keys메소드를 활용하는 건데요. 코드로는 다음과 같이 구현해볼 수 있습니다.
if n not in cache.keys():이제 피보나치 연산을 하면 됩니다. 형태는 이전에 재귀 함수에서 작성했을 때와 같습니다. 사전형으로 작성해야 한다는 것만 다르죠.
cache[n] = fib_memo(n-1, cache) + fib_memo(n-2, cache)이제 전체 코드와 예시를 봅시다.
def fib_memo(n, cache):
if n < 3:
return 1
if n not in cache.keys():
cache[n] = fib_memo(n-1, cache) + fib_memo(n-2, cache)
return cache[n]
def fib(n):
fib_cache = {}
return fib_memo(n, fib_cache)print(fib(10))
print(fib(100))55
354224848179261915075이번 시간에는 새로운 알고리즘 패러다임 Dynamic Programming과 이를 위한 조건 Memoization에 대해 배웠습니다. 배울 때는 어려웠던 재귀 함수가 참 많은 경우에 쓰이는 것 같네요.
다음 시간에는 Dynamic Programming의 또 다른 조건 Tabulation에 대해 배우고 두 조건 간의 차이점과 장단점에 대해 알아보겠습니다.
* 이 자료는 CODEIT의 '알고리즘의 정석' 강의를 기반으로 작성되었습니다.