알고리즘 평가법 2

지난 시간에는 알고리즘을 평가하는 두 기준과 평가에 필요한 기본적인 수학적 개념, 점근 표기법, 그리고 알고리즘 평가 사례에 대해 알아보았습니다. 이번 시간에는 주요 시간 복잡도와 공간 복잡도, 그리고 알고리즘 평가 시 주의해야 할 사항에 대해 함께 알아봅시다.

🧭 알고리즘 평가 주의 사항

점근 표기법으로 알고리즘을 평가할 때 몇 가지 주의 사항을 알려드리겠습니다.

❗ 인풋의 크기

앞서 인풋의 크기와 상관 없는 코드들에 대해 설명했었는데요. 여기서 '인풋의 크기와 상관 없다'는 말은 어떤 의미일까요?

이 말을 자세히 풀어서 설명하자면 '인풋의 크기와 상관 없이 동일한 시간 안에 실행되는 코드'라고 할 수 있습니다.

예를 들어, 리스트의 값을 꺼내오는 'my_list[i]'는 리스트 크기가 늘어나도 똑같은 시간 안에 실행됩니다.

그러나, 리스트를 정렬할 때 걸리는 시간은 리스트의 길이에 따라 달라지기 때문에 O(1)이 아닌 다른 시간 복잡도를 가지는 것이죠.

❗ 점근 표기법에서 n의 의미

점근 표기법에서 n이 갖는 의미는 뭘까요? 흔히 n을 인풋 크기를 나타낼 때 사용하곤 하지만 사실 별다른 의미는 없습니다. 인풋 크기를 x로 나타내면 O(x), O(x^2) 등으로 표기가 가능하니까요.

아직 자료 구조에 대해 배우진 않았지만 때로는 '트리'나 '그래프' 같은 특수한 자료 구조가 인풋값이 될 수 있습니다. 이들 자료 구조가 특수한 이유는 리스트처럼 선형적이지 않기 때문입니다.

예를 들어, 그래프는 꼭짓점과 변으로 이루어져 있습니다. 꼭짓점의 개수를 V, 변의 개수를 E라고 합시다. BFS는 두 꼭짓점 간 최단 경로를 찾는 알고리즘인데요. 이 알고리즘의 시간 복잡도는 O(V + E)로 나타냅니다. 시간 복잡도를 표현하기 위해 두 개의 다른 문자를 사용하고 있죠?

이처럼 편의상 n을 사용하는 것일뿐 n 자체에 특별한 의미는 없다고 보시면 됩니다.

❗ Big-O of 1 알고리즘

위 사례에서 대부분의 코드를 O(1)로 나타냈습니다. 그렇지만 모든 줄을 O(1)로 표기하는 것은 아닙니다. 앞에서 보았듯 인풋 크기와 상관 없는 코드만 O(1)로 나타내고 그렇지 않은 경우에는 시간 복잡도를 따져 봐야 합니다.

예를 들어, 정렬과 관련된 함수와 메소드인 sorted와 sort는 내부적으로 O(nlgn)을 가지고 있습니다. 또 다른 예로는 리스트에 요소가 있는지 확인하는 'in'이 있는데요. 'in'은 내부적으로 'O(n)'의 선형 탐색이 이루어집니다.

이후, 자료 구조 강의를 수강하면 더 많은 예시를 볼 수 있습니다.

❗ List Operations

리스트와 관련된 동작들의 평균 시간 복잡도를 봅시다. 여기서 리스트의 길이는 n입니다.

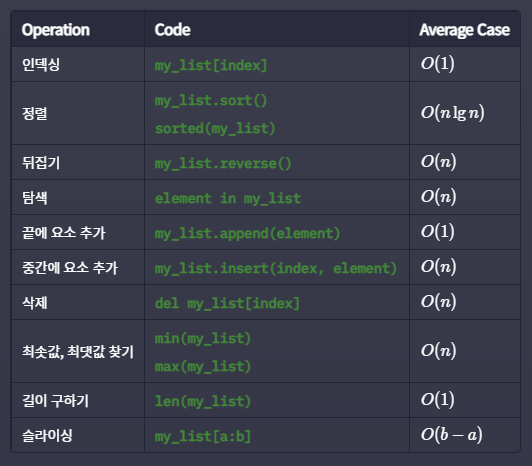
❗ Dictionary Operations

사전과 관련된 동작들의 평균 시간 복잡도를 봅시다.

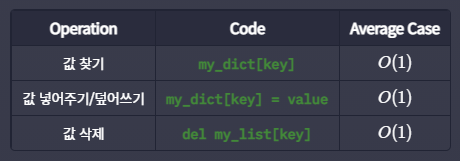
🧭 주요 시간 복잡도

동료 개발자와 협업하다보면 자연스레 시간 복잡도에 대해 논의하는 때가 생깁니다. 시간 복잡도를 계산할 줄 알아야 원활한 소통이 가능하죠.

대부분의 시간 복잡도는 이 중 하나입니다.

• O(1)
• O(lgn)
• O(n)
• O(nlgn)
• O(n^2)
• O(n^3)
• O(n^4)
• O(2^n)
• O(n!)

이 중에서도 블러 처리된 것들만 자주 사용되고 나머지는 흔치 않습니다.

❗ O(1)

O(1)은 인풋의 크기가 소요 시간에 영향을 미치지 않는 경우에 나타냅니다.

def print_first(some_list):
    print(some_list[0])
    
print_first([1, 2])
print_first([1, 3, 5, 7, 9, 11, 13, 15, 17, 19])

print_first 함수는 리스트 길이가 2든, 10이든 소요 시간이 같습니다. 어차피 맨 앞의 요소를 가져오기 때문에 리스트의 길이가 상관이 없는 것입니다. 이는 길이가 1억이 넘어가는 리스트를 받을 때도 마찬가지입니다.

팁을 주자면, 반복문이 없으면 대체로 시간 복잡도가 O(1)인 경우가 많습니다.

❗ O(n)

CASE 1. 반복문 & 반복 횟수가 인풋의 크기가 비례

def print_each(some_list):
    for i in range(len(some_list)):
        print(some_list[i])

CASE 2. n/2번 반복 -> O(1/2n) -> 점근 표기법 상, O(n)

def print_half(some_list):
    for i in range(len(some_list) // 2):
        print(some_list[i])

CASE 3. O(3n) -> 점근 표기법 상, O(n)

def print_three_times(some_list):
    for i in range(len(some_list)):
        print(some_list[i])
    
    for i in range(len(some_list)):
        print(some_list[i])
        
    for i in range(len(some_list)):
        print(some_list[i])

❗ O(n^2)

반복문 안에 반복문이 있고 둘 다 인풋 크기에 비례하는 경우, 시간 복잡도는 O(n^2)입니다.

def print_pairs(some_list):
    for i in range(len(some_list)):
        for j in range(len(some_list)):
            print(some_list[i], some_list[j])

❗ O(n^3)

같은 원리로, 인풋의 크기에 비례하는 반복문이 세 번 중첩되는 경우, 시간 복잡도는 O(n^3)입니다.

def print_triplets(some_list):
    for i in range(len(some_list)):
        for j in range(len(some_list)):
            for k in range(len(some_list)):
                print(some_list[i], some_list[j], some_list[k])

❗ O(lgn)

CASE 1. i가 두 배씩 증가

def print_powers_of_two(n):
    i = 1
    while i < n:
        print(i)
        i = i * 2

인풋 n이 64면 반복문이 총 몇 번 실행될까요? i가 1일 때부터 시작해서 2, 4, 8, 16, 32까지 총 6번 실행됩니다. 놀랍게도 lg64도 6입니다. 64를 2로 6번 나누어야 1이 되기 때문이죠.

이렇게 n이 log로 표현되는 경우, 시간 복잡도는 O(lgn)입니다.

CASE 2. i를 n부터 반씩 나누기

def print_powers_of_two(n):
    i = n
    while i > 1:
        print(i)
        i = i / 2

이번에는 i를 n부터 시작해서 반씩 나눠봅시다. 이 경우에도 i가 64일 때부터 시작해서 32, 16, 8, 4, 2까지 반복문이 6번 실행되어 마찬가지로 시간 복잡도는 O(lgn)입니다.

❗ O(nlgn)

앞서 O(n^2)이 O(n)과 O(n)을 중첩시킨 것임을 알았습니다. 같은 논리로 O(nlgn) 또한 O(n)과 O(lgn)이 겹쳐진 것입니다.

CASE 1. while문이 for문 안에 중첩

def print_powers_of_two_repeatedly(n):
    for i in range(n):
        j = 1
        while j < n:
            print(i, j)
            j = j * 2

여기서 for문의 반복 횟수는 n에 비례하고 while문의 반복 횟수는 lgn에 비례합니다. while문이 for문에 중첩되어 있기 때문에 시간 복잡도는 O(nlgn)입니다.

CASE 2. for문이 while문 안에 중첩

def print_powers_of_two_repeatedly(n):
    i = 1
    while i < n: 
        for j in range(n):
            print(i, j)
        i = i * 2

위 코드를 살짝 바꿔 이번에는 for문이 while문에 중첩되어 있습니다. 이 경우에도 시간 복잡도는 O(nlgn)입니다.

🧭 코드 없이 알고리즘 평가하기

지금까지 코드를 보며 알고리즘을 평가해봤습니다. 그런데 꼭 코드가 있어야만 알고리즘 평가가 가능한 것일까요? 유능한 개발자는 코드 없이 알고리즘을 떠올리기만 해도 시간 복잡도를 계산할 수 있다고 합니다.

결론을 말하자면 코드 없이도 알고리즘을 평가할 수 있습니다. 그 팁을 알려 드리겠습니다.

사실 선형 탐색 알고리즘 정도는 쉽게 시간 복잡도를 구해볼 수 있습니다. 인풋의 크기에 시간적 영향을 받는 코드만 추리면 되기 때문인데요. 대표적으로 반복문이 있었죠?

반복문을 제외한 나머지들은 통상 O(1)입니다. O(1)은 점근 표기법 상 나중에 생략될 가능성이 높기 때문에 반복문이 있는 코드는 반복문에만 초점을 두는 것이 좋습니다.

이런 식으로 생각하는 것이 익숙해지면 나중에는 코드가 총 몇 줄 있는지, 선언된 변수는 몇 개인지는 생각할 필요도 없이 바로 '선형 탐색을 하려면 최악의 경우에 n개를 봐야 하니까 O(n)이겠구나'라고 생각할 수 있습니다.

일단 내부적인 동작을 이해할 수 있다면 시간 복잡도를 구하는 일은 아주 쉽습니다. 애초에 점근 표기법 자체가 대략적으로 시간 복잡도를 구하는 것이었으니까요.

물론 조금 복잡한 알고리즘은 한 번쯤 꼼꼼히 따져봐야겠죠. 하지만 여러 코드를 대략적으로 평가하는 방법을 익히는 것은 알고리즘을 이해하는 데 많은 도움이 됩니다.

마지막으로 이진 탐색 알고리즘도 한 번 대략적으로 평가 해봅시다. 이진 탐색은 반복문이 돌수록 리스트의 길이가 반씩 줄어들었죠? 이를 바탕으로 '이진 탐색을 하려면 최악의 경우에 lgn개를 봐야 하니까 O(lgn)이겠구나'라고 생각할 수 있으면 됩니다.

🧭 공간 복잡도

앞서 시간 복잡도는 인풋 크기에 비례하는 알고리즘의 실행 시간을 나타낸다고 배웠습니다. 시간 복잡도 개념을 잘 이해하셨다면 공간 복잡도를 이해하는 것이 그리 어렵지 않을 것입니다.

공간 복잡도(Time Complexity)는 인풋 크기에 비례해서 알고리즘이 사용하는 메모리 공간을 나타냅니다. 시간 복잡도와 마찬가지로 공간 복잡도도 점근 표기법으로 표현이 가능합니다.

공간 복잡도에서 봐야 할 것은 파라미터와 변수입니다. 이들이 메모리를 차지하는 요소들이기 때문입니다.

❗ O(1)

def product(x, y, z):
    result = x * y * z
    return result

파라미터 x, y, z가 차지하는 공간을 제외하면 추가적으로 변수 result가 공간을 차지합니다. 그러나, result가 차지하는 메모리 공간은 인풋 크기와 무관하기 때문에 product 함수의 공간 복잡도는 O(1)입니다.

❗ O(n)

def get_every_other(some_list):
    every_other = some_list[::2]
    return every_other

인풋 some_list의 길이를 n이라고 합시다. 파라미터 some_list가 차지하는 공간을 제외하면 추가적으로 변수 every_other가 공간을 차지합니다. every_other가 차지하는 공간을 어떻게 표현할 수 있을까요?

리스트 every_other에는 some_list의 짝수 인덱스 값들이 복사되어 들어갑니다. 대략 n/2개의 값이 들어간다는 것이죠. O(n/2)는 점근 표기법 상 O(n)이 되기 때문에 함수 get_every_other의 공간 복잡도는 O(n)입니다.

❗ O(n^2)

def largest_product(some_list):
    products = []
    for x in some_list:
        products.append(x * y)
        
    return max(products)

인풋 some_list의 길이를 n이라고 합시다. 파라미터 some_list가 차지하는 공간을 제외하면 추가적으로 변수 products, x, y가 공간을 차지합니다. x와 y는 정수값을 가지고 있기 때문에 O(1)입니다. 그렇다면 리스트 products가 차지하는 공간은 어떻게 표현할 수 있을까요?

products에는 some_list에서 가능한 모든 조합의 곱이 들어갑니다. 결과적으로 총 n^2개의 값이 들어가겠죠? 따라서, 함수 largest_product의 공간 복잡도는 O(n^2)입니다.

주의할 것은 시간 복잡도와 공간 복잡도를 구하는 방식은 비슷하지만 두 개념이 항상 비례하는 것은 아닙니다. 시간 복잡도에 영향을 주는 것은 대체로 반복문이고 공간 복잡도에 영향을 주는 것은 파라미터와 변수니까요.

때로는 시간 복잡도가 O(n^2)이면서 공간 복잡도가 O(1)인 경우도 나옵니다. 그러니 두 개념이 마냥 비례한다고 생각하는 것은 위험하죠.

🧭 유용한 Python 기능 정리

마지막으로 시간 복잡도를 토대로 Python에서 유용한 기능들을 정리해보겠습니다.

❗ type

print(type(4))                # <class 'int'>
print(type(2.7))              # <class 'float'>
print(type[1, 3, 5, 7, 9])    # <class 'list'>
print(type(True))             # <class 'bool'>
print(type("True"))           # <class 'str'>

파라미터의 데이터 타입을 리턴해주는 함수 type의 시간 복잡도는 O(1)입니다.

❗ max, min

print(max[1, 10, 100])    # 100
print(min[1, 10, 100])    # 1

max 함수는 파라미터 중 가장 큰 값을 리턴하고 min 함수는 파라미터 중 가장 작은 값을 리턴해줍니다. 두 함수 모두 파라미터 개수가 유동적이기 때문에 원하는 만큼 넘겨 줄 수 있습니다.

파라미터 개수를 n이라 하면, 두 함수의 시간 복잡도는 O(n)입니다.

❗ str

some_str = str(12345)
print(some_str)          # 12345
print(type(some_str))    # <class 'str'>

str은 자료형을 문자열로 바꾸는 함수입니다.

파라미터를 n이라 하고, n의 자릿수를 d라고 합시다. 그럼 str 함수의 시간 복잡도는 O(logn)으로 나타낼 수 있고 O(d)로도 나타낼 수 있습니다.

O(logn)과 O(d)가 나오는 과정을 보여 드리겠습니다.

여기서 n은 정수 12345를 의미합니다. 이 정수는 현재 숫자 5개로 이루어져 있죠? str 함수를 이용해서 정수를 문자열로 변환하는데 걸리는 시간은 숫자의 크기가 아닌 자릿수에 비례합니다. 따라서 자릿수 d를 써서 표현하면 O(d)가 되는 것이죠.

그리고 12345는 10진법으로 표현된 수이기 때문에 자릿수가 몇 개인지를 따져보면 시간 복잡도가 O(log(10)n)이 됩니다. 이 말은 곧 O(logn)이 정수 n의 자릿수를 표현한다는 것입니다. 따라서, 자릿수 d와 log(10)n은 같습니다. 그래서 O(log(10)n)이 되는 것이죠.

❗ append, insert, del, index, reverse

some_list = [4, 7, 6, 5, 2]

some_list.append(8)    # 리스트 끝에 요소 추가
print(some_list)       # [4, 7, 6, 5, 2, 8]

some_list.insert(0, 1)    # 0번 인덱스에 요소 삽입
print(some_list)          # [1, 4, 7, 6, 5, 2, 8]

del some_list[0]    # 0번 인덱스 요소 삭제
print(some_list)    # [4, 7, 6, 5, 2, 8]

some_idx = some_list.index(8)    # 값의 인덱스 추출
print(some_idx)                  # 5

some_list.reverse()    # 리스트 뒤집기
print(some_list)       # [8, 2, 5, 6, 7, 4]

append의 시간 복잡도는 O(1)입니다. 나머지 함수들은 모두 O(n)입니다.

❗ sort, sorted

some_list = [4, 7, 6, 5, 2]

print(sorted(some_list))    # [2, 4, 5, 6, 7]
print(some_list)            # [4, 7, 6, 5, 2]

some_list.sort()
print(some_list)    # [2, 4, 5, 6, 7]

sort 메소드와 sorted 함수는 리스트를 정렬해줍니다. sorted 함수는 정렬된 새로운 리스트를 리턴해주고 sort 메소드는 그 리스트 자체를 정렬시켜준다는 차이가 있습니다.

둘 모두 시간 복잡도가 O(nlgn)입니다.

❗ slicing

some_list = [4, 7, 6, 5, 2]

print(some_list[2:4])     # [6, 5]
print(some_list[:4])      # [4, 7, 6, 5]
print(some_list[2:])      # [6, 5, 2]
print(some_list[:])       # [4, 7, 6, 5, 2]
print(some_list[::2])     # [4, 6, 2]

리스트 슬라이싱을 통해 리스트의 일부를 가져올 수 있습니다. 리스트 슬라이싱의 시간 복잡도는 슬라이싱 범위의 길이에 비례합니다. 따라서, some_list[x:y]의 시간 복잡도는 O(y-x)입니다.

❗ len

some_list = [4, 7, 6, 5, 2]
some_dict = {'a': 1, 'b': 2, 'c': 3, 'd': 4}
some_str = 'Hello World'

print(len(some_list))    # 5
print(len(some_dict))    # 4
print(len(some_str))     # 11

len 함수는 리스트, 사전, 문자열 등의 길이를 리턴해줍니다.

리스트와 사전, 문자열과 같은 자료 구조는 내부적으로 이미 저장되어 있어 len 함수 실행시 그대로 가져오기 때문에 시간 복잡도는 O(1)이 됩니다. 앞서 append가 O(1)인 것도 같은 이유에서 입니다.

---

이번 시간에는 알고리즘 평가 시 알아야 할 주의 사항과 주요 시간 복잡도, 그리고 코드 없이 알고리즘을 평가하는 방법과 공간 복잡도, 마지막으로 Python의 유용한 기능들의 시간 복잡도에 대해 알아 보았습니다.

시간 복잡도와 공간 복잡도는 다소 복잡한 개념일 수 있으나 알고리즘의 성능을 평가할 수 있는 개념인만큼 익혀두는 것이 중요합니다. 평소 코드를 작성할 때, 시간 복잡도를 대략적으로라도 구해보는 연습을 해보시길 바랍니다. 익숙해지면 많은 생각을 거치지 않고도 바로 구할 수 있습니다.

* 이 자료는 CODEIT의 '알고리즘의 정석' 강의를 기반으로 작성되었습니다.