아래 가족의 이름을 출력하는 함수 알고리즘은 호출 후,
완료되기까지 총 몇 번의 Step이 소요될끼?
const family = ['Hoon', 'Sun', 'Nam', 'In'];
function example(family) {
for (let i = 0;i < family.length;i += 1){
console.log(family[i]);
}
}
example(family);for 문을 통해 family 배열의 길이만큼 반복하면서 가족의 이름을 출력하고 종료되므로
총 4번의 step을 거쳐 알고리즘이 완료된다.
일이 언제 끝나는지 알려고 하는 행위는 매우 자연스럽고 중요한 일이다.
예를들어,
과제 제출까지 1시간도 남지 않았을 때,
다른 조건은 동일한데 30분만에 일을 처리해주는 계산기와
1시간동안 일을 처리해주는 계산기가 있다면
누구나 당연히 30분짜리 계산기를 사용할 것이다.
개발자가 문제를 해결하기 위해 알고리즘을 만들거나 선택할 때,
일이 언제 완료되는 알아야 상황에 맞게 알고리즘을 개선하거나 교체할 수 있다.
그럼 어떤 지표를 봐야 내가 선택하는 알고리즘이
빨리 일을 처리하는 알고리즘이라는 것을 알 수 있을까?
우린 이때 시간 복잡도를 보면 되고,
시간 복잡도 = 알고리즘 완료 Step의 수
라고 이해하면 된다.
우리는 이미 당장 위의 예시에서 시간 복잡도를 생각했었다.
"위 알고리즘은 총 4번의 step을 거쳐 동작이 완료된다."
라고 생각하는 것 자체가 시간 복잡도를 생각한 것이다.
그렇다면 어떻게 표현해야 모두가 알아들을 수 있을까?
표기법중 하나인 Big O
Big O 표기법은 알고리즘이 동작을 마무리하는데 걸리는 시간의 상한선,
즉 시간 복잡도의 상한선을 나타내는 표기법이다.
앞선 예시를 Big O로 표현하면 어떻게 될까?
가족 구성원이 6명인 입력의 경우,
알고리즘 완료까지 총 6 step이 필요할 것이다.
만약 대한민국 국민의 이름들을 넣어도
알고리즘 완료까지 대략 5000만번의 step이 필요할 것이다.
이처럼 입력이 커져도 일을 처리하는데 걸리는 step이 일정하게 증가하는 시간 복잡도를
Constant complexity 라고 하며, O(1)으로 표기할 수 있다.
이처럼 시간 복잡도는 입력의 크기에 따라 일 처리 step이 얼만큼 바뀌는지 를 표현하는 지표이다.
이 느낌만 잡으면 다른 알고리즘의 표현은 금방 감을 잡을 수 있다.
아래는 js로 작성된 이진 검색 알고리즘이다.
const binarySearch = (list, target, left, right) => {
let mid = 0;
while (left <= right) {
// 가운데 인덱스
mid = Math.floor((left + right) / 2);
if (list[mid] === target) {
return mid;
}
// 대소 비교로 범위 지정
if (list[mid] > target) {
right = mid - 1;
} else {
left = mid + 1;
}
}
return -1;
}
const sample = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10];
sample.sort((a, b) => a - b);
// ( 찾을 배열, 탐색할 값, 시작점, 끝점 )
const result = binarySearch(sample, 7, 0, sample.length - 1);
console.log(result);
이진 검색 알고리즘은 정렬된 데이터를 받은 후,
데이터의 중간값과 찾고자하는 값을 계속해서 비교하면서,
찾는 값이 있는 방향으로 1/2씩 범위를 좁혀나가며 검색하는 알고리즘이다.
알고리즘 전체 일을 1로 보았을 때,
해당 알고리즘의 입력 N과 step k의 관계식을 고려하면,
N 길이의 입력에서 원하는 값을 찾을 때까지,
1/2씩 감소시켜가며 데이터를 찾으므로
N*(1/2)^k = 1
로 표현할 수 있다.
step이 결국 시간 복잡도이므로, step k를 구하면
k = log N = O(log N)
으로 이진 검색 알고리즘의 시간 복잡도를 Logarithmic complexity로 표현할 수 있다.
아래 그래프를 보면,
앞선 Constant complexity보다 Logarithmic complexity가
일 처리하는데 시간이 덜 걸린다는 것을 알 수 있다.
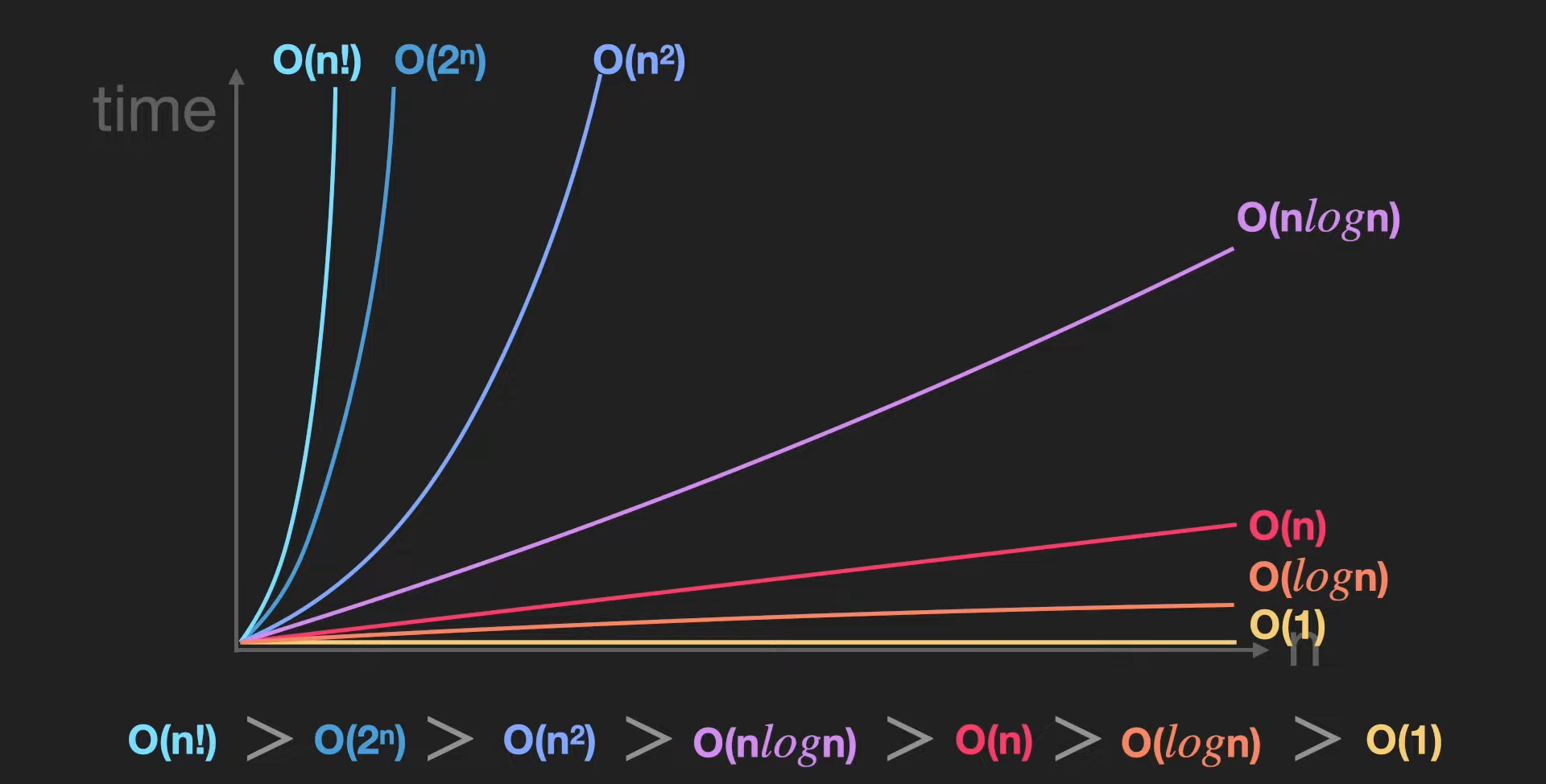
위의 방식대로 생각했을 때 각 표현법에 대해서 설명해 보았다.
Constant complexity O(1)
- 상수 시간, 입력에 관계 없이 완료까지의 절차가 동일
linear complexity O(n)
- 1차 시간, 입력이 커지면 완료까지의 절차가 선형적으로 증가
Quadratic complexity O(n^2)
- 2차 시간, 입력이 커지면 완료까지의 절차가 n^2 단위로 증가
Logarithmic complexity O(log N)
- 로그 시간, 입력이 2배면 완료까지의 절차가 1 증가하는 log n 단위로 증가
만약 입력이 여러 개라면 시간 복잡도 표현은 어떻게 될까?
각 입력의 변화애따라 시간 복잡도가 달라지므로,
아래 자료처럼 입력마다 각각 다른 변수를 두고 합과 곱으로 나타낸다.

cf. big O는왜 많이 쓸까?
- lower bound대로 동작하면 좋지만 upper bound에 대한 대비를 해야하기 때문
참고자료

감사합니다. 이런 정보를 나눠주셔서 좋아요.