[BOJ] 1300 k번째 수

soooooyeon·2021년 4월 29일

백준 알고리즘 이분탐색

문제

입력

문제

세준이는 크기가 N×N인 배열 A를 만들었다. 배열에 들어있는 수 A[i][j] = i×j 이다. 이 수를 일차원 배열 B에 넣으면 B의 크기는 N×N이 된다. B를 오름차순 정렬했을 때, B[k]를 구해보자.

배열 A와 B의 인덱스는 1부터 시작한다.

입력

첫째 줄에 배열의 크기 N이 주어진다. N은 105보다 작거나 같은 자연수이다. 둘째 줄에 k가 주어진다. k는 min(109, N2)보다 작거나 같은 자연수이다.

출력

B[k]를 출력한다.

처음 접근 방법 (오답)

1부터 n*n의 수까지, n 이하의 두 수(i, j)의 곱으로 만들 수 있는 경우의 수를 하나씩 세서 cnt에 반영하고,
cnt == k 일 때 값 출력하기
-> 이렇게 했을 때의 코드는 아래와 같다.

int n, k;

int main() {
    cin.tie(0);
    cout.tie(0);
    ios::sync_with_stdio(false);

    cin >> n >> k;

    int cnt = 0;

    for(int i = 1; i <= n*n; i ++) { // 1부터 n*n까지의 수가 있을 수 있기 때문
        for(int j = 1; j <= n; j++) {
            if(i%j == 0 && i/j <= n) {
                cout << i <<" "<<j << endl;
                cnt ++;
            }
        }
        if(cnt >= k) {
            cout << i << endl;
            exit(0);
        }

    }



    return 0;
}

답을 제출하지 않아도 시간초과인 것을 알 수 있었다.
n*n (n <= 100000) 번 for문을 돌고, 그 안에서 최대 n번 for문을 돌고 있으니 시간 복잡도는 O(10^15)로 2초를 넘기고도 충분했다^^

접근 방법 (정답)

"i보다 작거나 같은 수의 갯수"를 구하는게 관건이었다.
i = 6이고, n = 5 일 때, 배열 A의 원소를 나열해보면 다음과 같다.

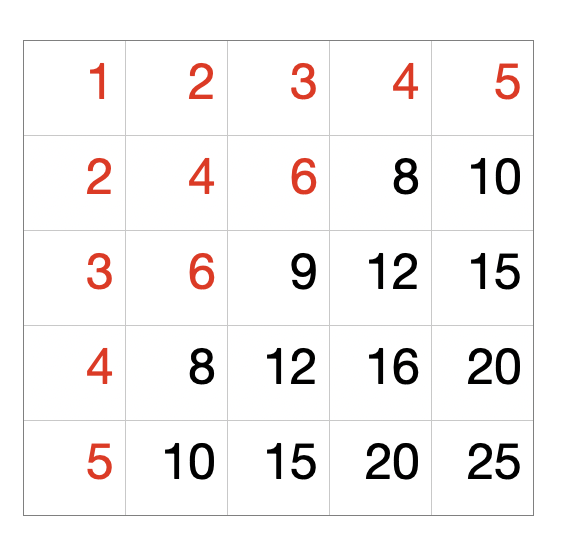
이 때, 1열에서 6보다 작은 수는 (1,1) ~ (1, 5)에 있는 수 5개이다.
-> min(n, i/1) = min(5, 6) = 5

2열에서 6보다 작은 수는 2, 4, 6 총 3개이다.
-> min(n, i/2) = min(5, 3) = 3

3열에서 6보다 작은 수는 3, 6 총 2개이다.
-> min(n, i/3) = min(5, 2) = 2

이렇게, 모든 행에 대해 i / (행의 번호)를 계산한 결과를 더하면 i 이하의 수의 갯수를 구할 수 있다.

이 때, i 이하의 수를 구하는 일정한 규칙(?)이 없기 때문에 이분 탐색을 통해서 적절한 i를 고르면 된다

풀이

#include <iostream>
#include <algorithm>
#include <stack>
#include <string.h>
#include <vector>
#include <map>
#include <math.h>
#include<queue>

using namespace std;
long n, k;

long numberBelow(long i) {
    long sum = 0;
    for(int j = 1; j <= n; j++) {
        sum += min(n, i/j);
    }
    return sum;
}

long exactNumber(long i) {
    long sum = 0;
    for(int j = 1; j <= min(n, i); j++) {
        if(i%j == 0 && i/j <= n) sum ++;
    }
    return sum;
}

int main() {
    cin.tie(0);
    cout.tie(0);
    ios::sync_with_stdio(false);

    cin >> n >> k;

    long l = 1;
    long r = n*n;
    long answer = 0;

    while(l <= r) {
        long m = (l + r)/2;
        long v = numberBelow(m);
        long cnt = exactNumber(m);

        if(v >= k) {
            if(v - cnt < k && cnt != 0) {
                answer = m;
                break;
            } else r = m-1;
        } else {
            l = m+1;
        }
    }

    cout << answer << endl;


    return 0;
}