https://www.acmicpc.net/problem/2571
분할정복보다는 누적합에 더 가까운문제였던것같다..

메인로직은 다음과같다..
높이를 세운 누적합 문제라고 보면 편할꺼같다..
그림으로 쉽게 이해해보자

다음과 같이 사각형이 있다면
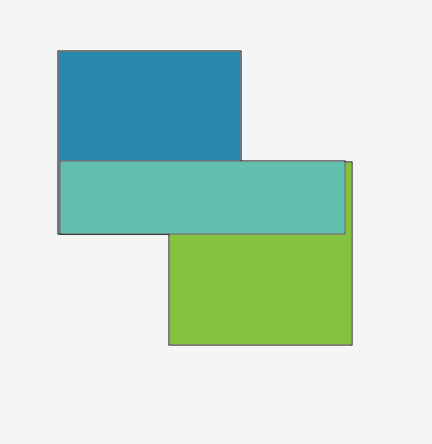
가운데 청록색을 구하는게 이번문제의 핵심이다..
그렇다면 누적합을 사용하기위해 파랑색과 녹색의 값을 111로 초기화해보자

누적합을 적용할 방향은 상관없으나 편하게 세로로 넣도록 하겠다..
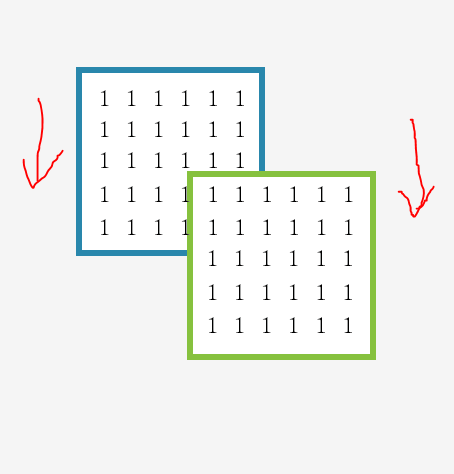
계산 결과는 다음과같이된다
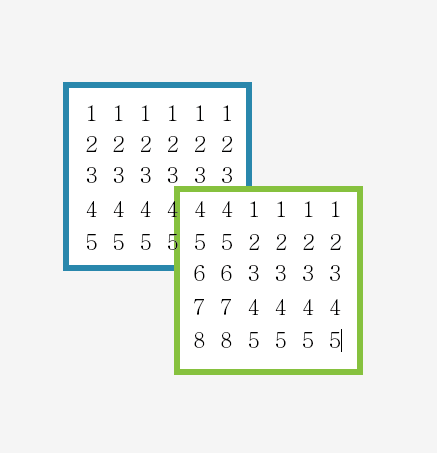
그다음 이제 각 원소마자 검사를 해주면 길이의 최대가 나온다..
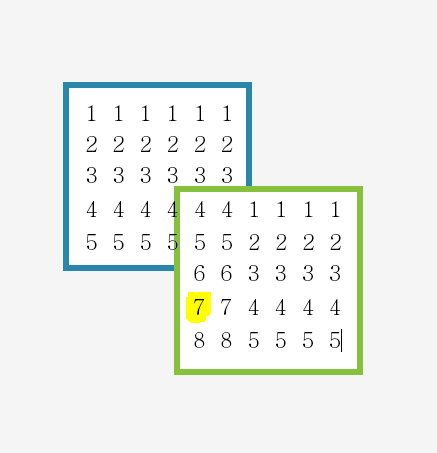
해당 지점을 검사한다고하면..
-
첫번째 검사
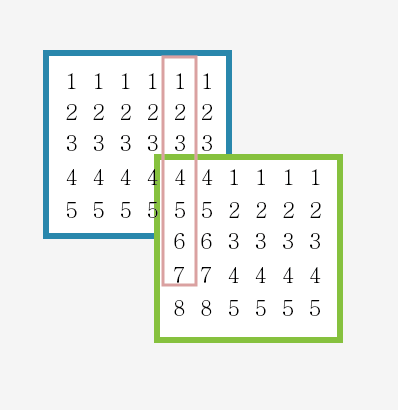
-
2번쨰검사..
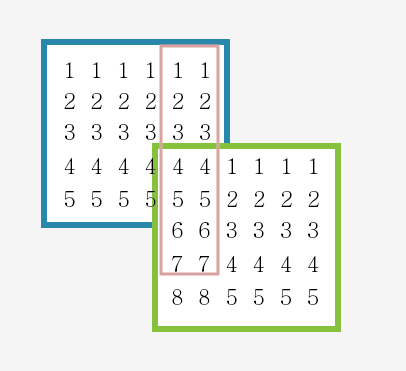
-
3번쨰 검사를 하려고하는데..다음과같은문제가발생..
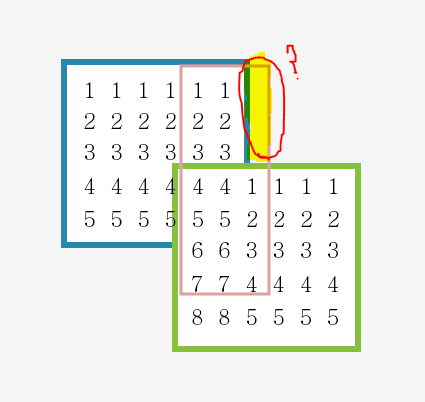
그래서 작은값으로 '4' 로 사이즈조절을 다시해준다..
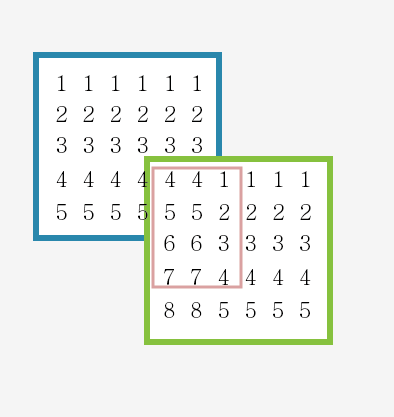
이렇게 각 좌표마다 n만큼 검사를해주면된다..
그러면 O(n^2) " 모든 좌표 검사 " * O(n) " 해당좌표에서 n만큼 사각형 크기 검사 "
=> O(n^3)
그러면 그냥 모든 좌표에다가 바로바로 검사해서 낮은값으로 하면안되나요?
방금같은경우도 그냥 좌표중에 '4' 찾고 그냥 다 구하면되잖아요!
답은 => 4의 값으로 줄이기전에 7의값으로 구성하는게 더 클수도있고...
중간에 값이 없는 경우도 있을수 있기때문에 n^3으로 구성되어야된다..
그림으로 설명하면..
엣지케이스
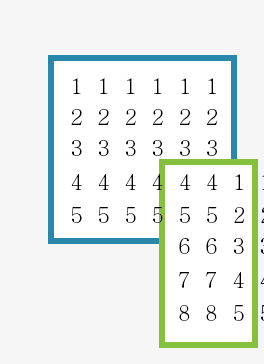
라고하면 ..
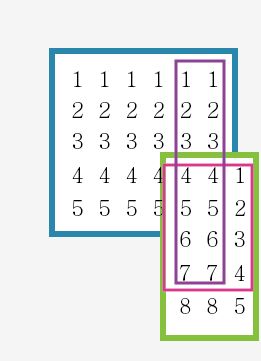
분홍색 4 3 = 12
보라색 7 2 = 14
그리고 중간에 없는경우..
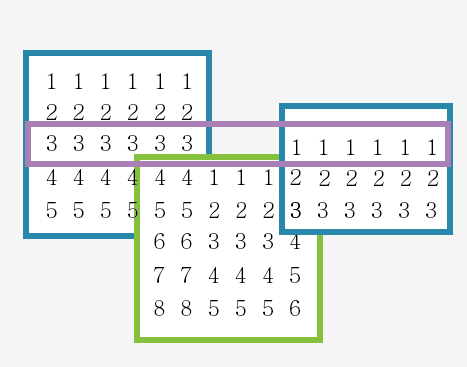
이런경우이다.. 그래서 결국은 n^3 검사를 해주는게 포인트..
정리해서 설명하면 메인로직은 다음과같다.
메인로직
- 누적합구하기 (n^2)
- 누적합중에 최대 넓이 구하기 (n^3)
- 끝
로직자체는 간단하다.
코드는 다음과같다..
import java.util.*;
import java.io.*;
public class 색종이3 {
static int array[][];
static int N;
static int answer;
public static void main(String[] args) throws Exception{
// TODO Auto-generated method stub
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
N= Integer.parseInt(br.readLine());
answer =-1;
array = new int[100][100];
for(int i=0;i<N;i++) {
st= new StringTokenizer(br.readLine());
int x = Integer.parseInt(st.nextToken());
int y = Integer.parseInt(st.nextToken());
for(int a=x;a<x+10;a++)
for(int b=y;b<y+10;b++) {
array[a][b] = 1;
}
}
acc();
sum();
System.out.println(answer);
}
public static void print() {
for(int i=0;i<100;i++) {
for(int j=0;j<100;j++) {
System.out.print(array[i][j]+ " ");
}
System.out.println();
}
}
public static void acc() {
for(int i=0;i<99;i++) {
for(int j=0;j<100;j++) {
if(array[i][j]!=0 && array[i+1][j]!=0) {
array[i+1][j] = array[i][j] +1;
}
}
}
}
public static void sum() {
for(int i=0;i<100;i++) {
for(int j=0;j<100;j++) {
int h = 100;
for(int k=j;k<100;k++) {
h= Math.min(array[i][k], h);
if(h==0) break;
answer = Math.max(answer, h*(k-j+1));
}
}
}
}
}
분할정복은.. 어려운건 너무손도못대겟고..이걸로 시간잡히는게 쫌그래서..
다른 챕터를 한바퀴돌고와서 심화문제를 풀도록해보자.. 다음은.. dp이다!
