백준 2629 양팔저울

https://www.acmicpc.net/problem/2629

// 사담

진짜 수많은 트라이가있엇고 답을 봣지만 0-1 knapsack.. 그리고 dp 점화식 풀이.. 혹은 dfs 풀이..

하지만 knapsack으로 분류된 이유가있고.. 0-1 knapsack말고 고집을 부려서 풀고싶었고.. 그과정에서 좀 더럽게 풀긴했다..

그래도 수많은 시도가 아까우니까 접근과정에 대해서 적을까한다.,.

---

공통 메인 아이디어

해당 무게를 측정하기위해 왼쪽에 있다고 가정하고 fix를 한다면

왼쪽에 추를 올려서 무게를 재는경우 (추무게 + 현재무게 )

오른쪽에 올려서 마이너스로 구하는경우 (추무게 - 현재무게)

이과정에서 마이너스를 구하는경우 음수값이 나오는데 이경우는 못구하는게 아니다.. why?

추무게 3 현재무게 50이면 -47이나오지만 반대로 생각하면 47만큼 구할수있다는뜻 -> 그래서 abs적용하기

---

첫번째 시도

해당 결과를 가지고 knapsack을 세웠다..

		for(int i=0;i<k;i++) {
			for(int j=15000;j>0;j--) {
				if(result[Math.abs(j-v[i])]) result[j] = true;
				if(j+v[i]<=15000) {
					if(result[j+v[i]]) result[j] = true;
				}
			}
		}
		

왜 안되는지 몰랐다... 그러나 곰곰히 생각해보면

첫번째 if문에서 뺀값을 가지고 두번째 if문에서 더하기 했을때 중복 사용이 되는게 아닌가 ??
라고 생각해서 순서를 바꿔보았다..

두번째시도

		for(int i=0;i<k;i++) {
			for(int j=15000;j>0;j--) {
            	if(j+v[i]<=15000) {
					if(result[j+v[i]]) result[j] = true;
				}
				if(result[Math.abs(j-v[i])]) result[j] = true;
			}
		}
		

당연히 실패 그러나 중복에 대한 문제가 맞았다.. 그래서 간단하게 그림으로보면

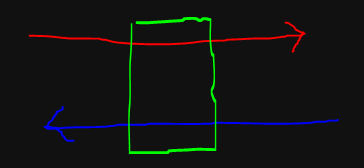
물론 이런식으로 진행되는건 아니지만 j+v[i] 값 기준으로 보게된다면 (빨간색선)

기존의 진행한 j-vi 값으로 만들어진 초록색부분을 사용하게되면 추가 중복사용하게되는것이였다.

그래서 추의 중복의 문제여서 visited로 중복을 체크해주면 되는걸까? 하고 다음과같이고쳤다..

		for(int i=0;i<k;i++) {
			for(int j=15000;j>=0;j--) {
				int cur = Math.abs(j-v[i]);
				if(result[cur] && !visited[cur][i]) {
					result[j] = true;
					visited[j][i] = true;
				}

				if(j+v[i]<=15000) {
					cur = j+v[i];
					if(result[cur] && !visited[cur][i]) {
						result[j] = true;
						visited[j][i]=true;;
					}
				}
			}
		}

visited[젤추의값][사용한추의번호]

추를 0번부터 사용했기때문에 visited[20][3] => 20의 무게를 재기위해 0 번 1번 2번 3번추까지 사용한 결과

그리고 초기화는 이전의 추에서 + 무게를 더한거까지 쓰므로 저렇게 true 처리를 하고 진행하면된다!!

결과는 => 성공

해당 로직 바탕으로 코드는 다음과 같다..

import java.io.*;
import java.util.*;

public class 양팔저울 {

	public static void main(String[] args) throws Exception{
		// TODO Auto-generated method stub
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		int k = Integer.parseInt(br.readLine());
		
		StringTokenizer st = new StringTokenizer(br.readLine());
		
		int max = 40001;
		
		boolean[] result = new boolean[max];
		boolean[][] visited = new boolean[15001][k];
		int[] v = new int[k];
		int[] w = new int[k];
		for(int i=0;i<k;i++) {
			int cv = Integer.parseInt(st.nextToken());
			v[i] = cv;
			// result[cv] = true;
		}
		
		result[0] = true;
		
		
		for(int i=0;i<k;i++) {
			for(int j=15000;j>=0;j--) {
				int cur = Math.abs(j-v[i]);
				if(result[cur] && !visited[cur][i]) {
					result[j] = true;
					visited[j][i] = true;
				}

				if(j+v[i]<=15000) {
					cur = j+v[i];
					if(result[cur] && !visited[cur][i]) {
						result[j] = true;
						visited[j][i]=true;;
					}
				}
			}
		}
		
		
		int t = Integer.parseInt(br.readLine());
		st = new StringTokenizer(br.readLine());
		StringBuilder sb =new StringBuilder();
		for(int i=0;i<t;i++) {
			int cv = Integer.parseInt(st.nextToken());
			if(result[cv]) {
				sb.append("Y ");
			}
			else {
				sb.append("N ");
			}
		}
		System.out.println(sb);
		
	}
}

ㅎㅎㅎ..... knapsack을 어느정도 이해한 수준에 올른것같다.. 그리디로 넘어가자!