사용 언어: python 3.9.1

❓ Problem

백준 1629. 곱셈

📕 피드백

1. 발전 방향

symmetric한 경우인 지 잘 살펴보고 맞다면 한쪽에 대해 재귀함수를 돌린 값을 재활용한다.

2. 느낀점

분할정복은 재귀. 그런데 이 경우 양쪽으로 갈라서서 두쪽에 대해 재귀를 돌리는 게 아님. symmetric하니까!! symmetric한 경우라는 건 곧 두쪽이 비슷한 결과를 낸다는 것이고, 그 두쪽에 대해 다 재귀함수를 호출할 필요가 없다는 것임. 즉, 중복이라는 것.

🚩 Solution

1. 접근법

TRY 1

pow 이용. 2%까지 갔다가 시간초과.

TRY 2

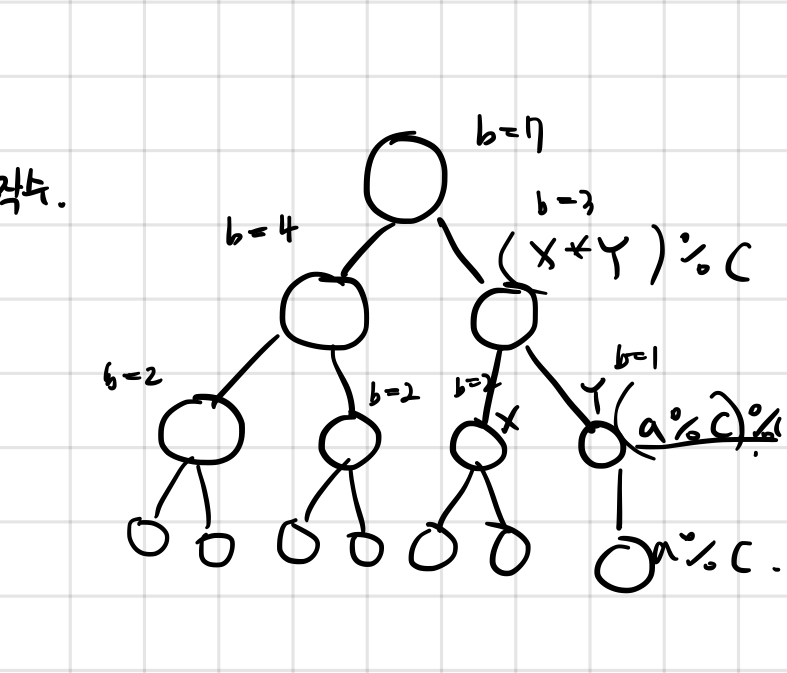
분할정복 이용, 시간 초과. pow를 사용했을 때와 동일한 시간복잡도가 이유라고 추정

TRY 3

left_remain = right_remain * a 이므로 right_remain을 재귀로 구했으면 left_remain도 자연스럽게 구할 수 있음(symmetric한 경우이므로)

TRY 4

그런데 홀수의 경우와 짝수인 경우가 다름!

생각해 보면 홀수의 경우: 왼쪽은 N//2+1이고, 짝수의 경우: 왼쪽은 N//2임.

따라서 left_remain을 짝수인 경우와 홀수인 경우로 나눠서 right_remain값(재귀로 알아낸 값)으로부터 도출

2. 코드

import sys; read = sys.stdin.readline

A, B, C = tuple(map(int, read()[:-1].split(" ")))

def findRemain(a, b):
    # 종결조건
    if (b==1):
        return a%C
    else:
        right_remain = findRemain(a, b//2); left_remain = right_remain*a if b%2 == 1 else right_remain
        return (left_remain*right_remain)%C

print(findRemain(A%C, B))

3. 결과

시간 복잡도 분석

O(logB)