105. Construct Binary Tree from Preorder and Inorder Traversal

문제링크: https://leetcode.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/

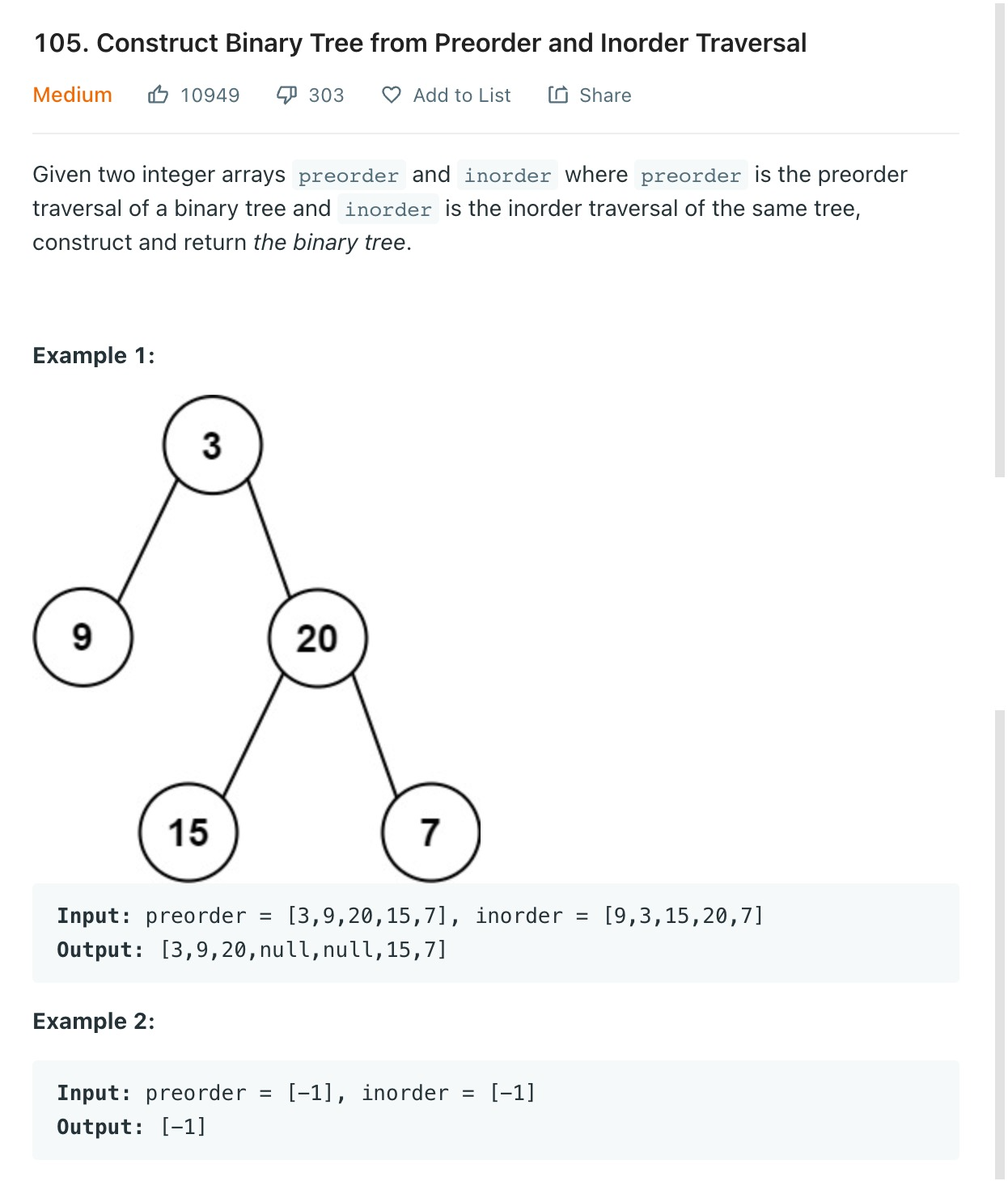
전위순회와 중위순회의 값을 통해 원본 트리를 완성한다. 이 때, 노드의 값들은 중복되지 않음.

Solution

1. Get head and recurse

preorder에서 얻을 수 있는 정보: 맨 앞의 원소가 트리의 루트노드(부모 노드)가 된다.
inorder에서 얻을 수 있는 정보: 부모노드를 기준으로 왼쪽노드와 오른쪽 노드를 분리할 수 있다.
위 두가지 특성을 이용해 주어진 배열에서 가장 위 부모노드와 좌, 우의 자식노드로 구별할 수 있다.

Algorithm

• 전위순회와 중위순회 모두 부모노드수 1+ 왼쪽자식의 노드수 를 합한 값은 같기 때문에 inorder에서 얻은 부모의 index가 preorder에서 왼쪽 자식노드의 끝이 된다.
• 부모노드를 뺀 나머지 왼쪽, 오른쪽 자식노드의 배열을 통해 다시 buildTree를 할 수 있다.
• 재귀를 통해 좌측노드를 buildTree(preorder.slice(1, parentIndex + 1), inorder.slice(0, parentIndex)), 우측 노드를 buildTree(preorder.slice(parentIndex + 1), inorder.slice(parentIndex + 1)) 로 구할 수 있다.

var buildTree = function(preorder, inorder) {
  // preorder: 뭐가 root인지 알 수 있다. (맨 앞)
  // inorder : 뭐가 root의 왼쪽인지 알 수 있다. (root의 앞 원소들)
  // 1. preorder를 통해 root를 얻는다.
  // 2. inorder를 탐색하면서 root값을 만날 때까지 간다.
  // 3. inorder가 root를 만날때 까지의 값들은 leftchild, head이후의 값들은 rightchild가 되고 재귀를 반복한다.
  if (preorder.length === 0) return null;
  // left parent right
  const parent = preorder[0];
  const parentIndex = inorder.indexOf(parent);
  const result = new TreeNode(
    parent, 
    buildTree(preorder.slice(1, parentIndex + 1), inorder.slice(0, parentIndex)), 
    buildTree(preorder.slice(parentIndex + 1), inorder.slice(parentIndex + 1))
  );
  
  return result;
};

2. Recurse with index

1번 방식은 매번 slice를 통해 새 배열을 만드는데 이는 공간과 시간을 추가적으로 사용한다. slice대신 index만 전달하는 방식으로 만든다면 같은 정보를 전달하면서도 공간과 시간을 절약할 수 있다.(slice는 O(n)의 시간, 공간복잡도를 가진다.)

Algorithm

• buildTreeWithIndex함수는 배열 대신 인덱스만 가지고 위와 같은 동작을 수행한다.
• 부모노드를 정하고 indexOf대신 반복문을 통해 좌우측 자식 노드를 나누는 기준을 구한다.
• parentIndex를 통해 좌우측을 나누고 자식 노드들도 생성한다. 이 때, preOrder의 중간 인덱스는 preLeft + parentIndex - inLeft가 된다.

var buildTree = function(preorder, inorder) {
  // 인덱스만 전달해서 효율적으로 build하기
  const buildTreeWithIndex = (preLeft, preRight, inLeft, inRight) => {
    if (preLeft > preRight || inLeft > inRight) return null;
    const parent = preorder[preLeft];
    let parentIndex;
    // Get parentIndex
    for (let i = inLeft; i <= inRight; i++) {
      if (inorder[i] === parent) {
        parentIndex = i;
        break;
      }
    }
    return new TreeNode(
      parent,
      buildTreeWithIndex(
        preLeft + 1, 
        preLeft + parentIndex - inLeft, 
        inLeft, 
        parentIndex - 1),
      buildTreeWithIndex(
        preLeft + parentIndex - inLeft + 1, 
        preRight, 
        parentIndex + 1, 
        inRight)
    );
  }
  
  return buildTreeWithIndex(0, preorder.length - 1, 0, inorder.length - 1);
};

1번의 방식보다 시간, 공간적으로 크게 개선되었다. 전체적인 시간 복잡도는 parent를 정하는 횟수는 총 n 번, parent가 정해질 때마다 반복문을 통해 inOrder에서 parent index를 구하게 되는데 이 길이는 점점 반이 된다. 첫 실행에서 n, 두세번째에서 n/2 합 n, 다음 4번은 n/4 *4 합n이 된다. 1번실행 = n , 2,3 = n, 4,5,6,7 = n 의 방식의 n의 총 횟수는 logn이 되고 총 시간복잡도는 O(nlogn)이 된다.

3. Use map to get index

2번에서 반복문을 통해 inorder의 parent 인덱스를 구했는데, inorder의 val => index 의 map을 만든다면(inorder의 값은 unique) O(1)의 시간으로 인덱스를 얻을 수 있고, 전체적으로 O(n)의 시간복잡도를 가지게 된다. 대신 추가적으로 O(n)의 공간복잡도를 가진다.

var buildTree = function(preorder, inorder) {
  // 인덱스만 전달해서 효율적으로 build하기
  const myMap = new Map();
  inorder.map((el, idx) => myMap.set(el,idx));
  
  const buildTreeWithIndex = (preLeft, preRight, inLeft, inRight) => {
    if (preLeft > preRight || inLeft > inRight) return null;
    const parent = preorder[preLeft];
    // Get parentIndex
    const parentIndex = myMap.get(parent);
    return new TreeNode(
      parent,
      buildTreeWithIndex(
        preLeft + 1, 
        preLeft + parentIndex - inLeft, 
        inLeft, 
        parentIndex - 1),
      buildTreeWithIndex(
        preLeft + parentIndex - inLeft + 1, 
        preRight, 
        parentIndex + 1, 
        inRight)
    );
  }
  
  return buildTreeWithIndex(0, preorder.length - 1, 0, inorder.length - 1);
};