124. Binary Tree Maximum Path Sum

문제링크: https://leetcode.com/problems/binary-tree-maximum-path-sum/

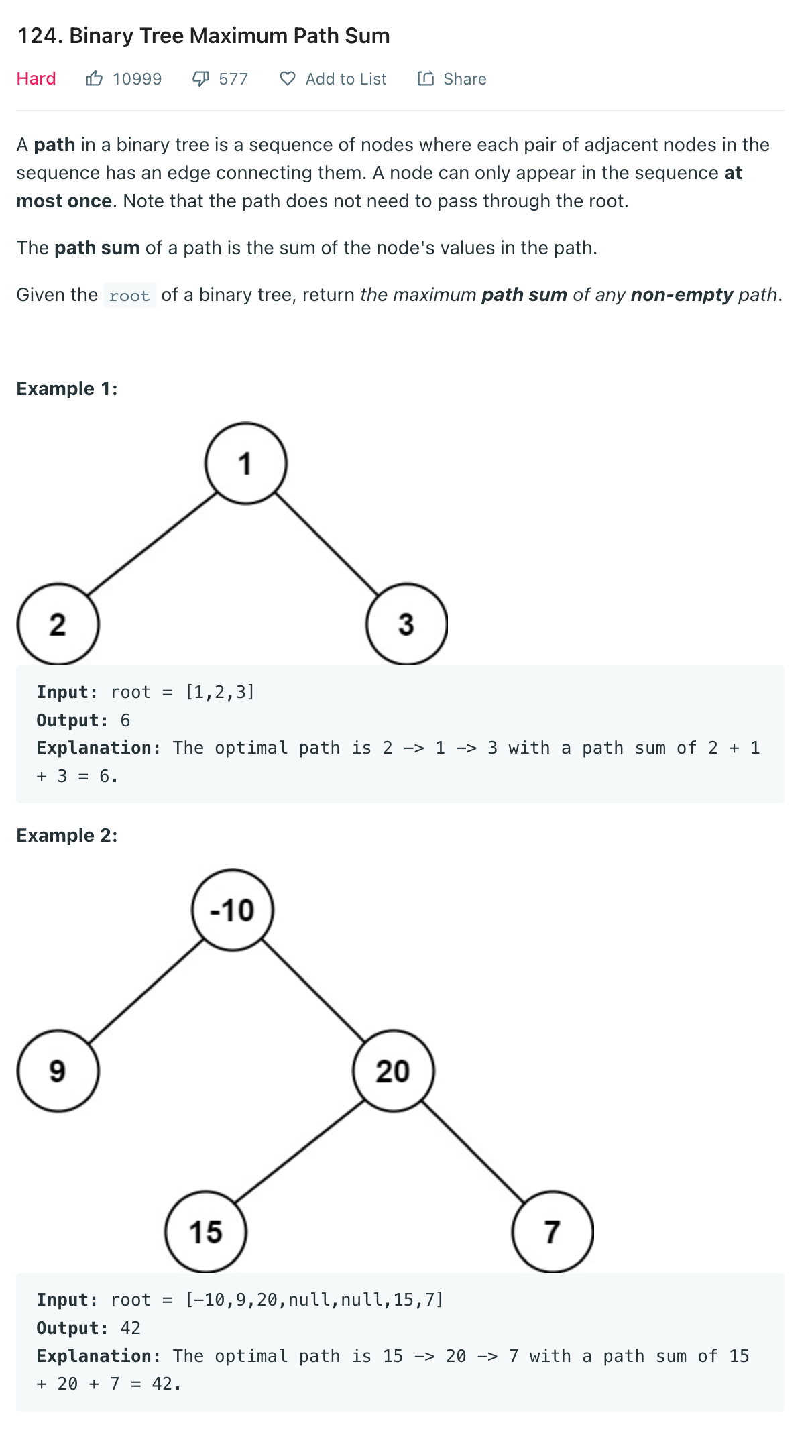
노드의 연결을 통해 합이 최대가 되는 합을 도출하는 문제다.
시작은 어느 곳에서 해도 되며 한번 연결한 노드를 재방문 할 수 없다.

Solution

DFS & Bottom-up

꼭 루트에서 시작할 필요는 없기 때문에 상단루트에서는 정보를 얻기 쉽지 않다. 하지만 반대로 리프에서는 리프->차일드 로 연결할 경우 리프값이 최대값이 되기 때문에 Bottom-up 관점으로 문제를 볼 수 있다.
아래서 부터 문제를 접근하면 자녀와 현재노드가 주어질 때 자녀 중 하나를 골라 현재 노드까지의 최대 합을 구할 수 있고 추가적으로 왼쪽 - 노드 - 오른쪽으로 통하는 연결의 최대 합도 구할 수 있다.
노드까지의 최대 합의 경우 새로운 부모를 만났을 때 다른 자녀와 비교를 해 부모까지 연결하는 최대 합을 구할 수 있다.
해당 방식을 후위 순회를 통해 구현하기로 했다.

Alogrithm

• DFS의 후위 순회를 통해 자녀의 값(자녀까지 연결되는 최대합)을 먼저 구한다.
• 탐색하려는 노드가 없을 경우는 0을 반환한다.
• 자녀까지 연결되는 최대값을 구하면 현재 노드의 최대값은 현재 + MAX(0, 왼쪽, 오른쪽) 가 된다.
• 추가적으로 현재 노드를 통과하는 왼쪽 - 현재 - 오른쪽 의 연결값도 구할 수 있다.
• 윗 값들을 통해 현재 구할 수 있는 최대값을 갱신하고 순회를 이어간다.

var maxPathSum = function(root) {
    // bottom-up
    // 후위순회를 이용해 연산
    // 기본 알고리즘: 선택한 노드를 시작으로 child로 연결하는 링크의 최대 크기를 비교
    let totalMaxSum = -Infinity;
    // getMaxSumStartFromHere
    const dfs = (node) => { 
        if (!node) return 0;
        const leftSum = dfs(node.left);
        const rightSum = dfs(node.right);
        
        // Child + Node의 최대 (현재val 단독 or child 중 큰것과 비교)
        const maxSum = node.val + Math.max(leftSum, rightSum, 0);
        
        // 좌우 child를 연결한 결과 갱신 MAX(현재값, 현재노드~차일드값, 왼쪽 - 현재노드 -오른쪽)
        totalMaxSum = Math.max(totalMaxSum, maxSum, leftSum + rightSum + node.val);
        
        return maxSum;
    }
    
    dfs(root);
    return totalMaxSum;
};