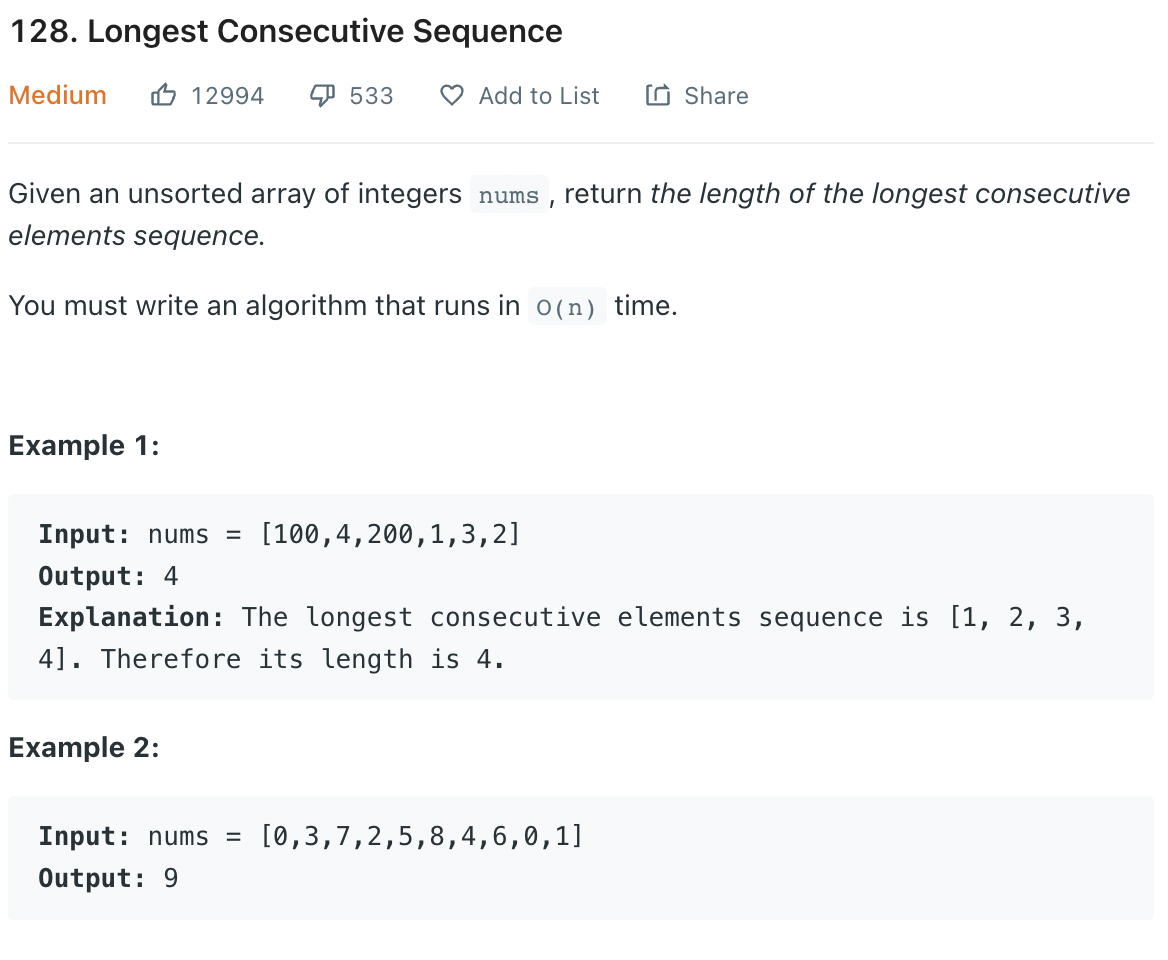
128. Longest Consecutive Sequence

문제링크: https://leetcode.com/problems/longest-consecutive-sequence/

Solution

1. Union Find

Union Find를 이용해 연속적인 원소가 나타났을 때 ex)234'5' 부모를 동일하게 묶어 동일한 부모는 연속적인 수임을 나타낼 수 있다.

Algorithm

• nums의 부모를 저장할 myMap을 만든다
• getHead는 최종 부모를 얻는 함수, union은 최종부모를 동일하게 묶는 함수다.
• nums를 순회하면서 myMap에 num + 1 이나 num - 1이 존재할 경우 둘을 union한다.
• 각 원소들의 부모를 탐색해 부모에 따른 자식의 수를 카운트한다.
• 가장 큰 카운트가 가장 긴 sequence의 길이다.

var longestConsecutive = function(nums) {
  // 연이은 숫자
  // union
  const myMap = new Map(); // num => headNum union느낌?
  const getHead = (num) => {
    let el = num;
    while (myMap.get(el) !== el) {
      el = myMap.get(el);
    }
    return el;
  }
  const union = (num1, num2) => {
    myMap.set(getHead(num2), getHead(num1));
  }
  
  for (let num of nums) {
    if (!myMap.has(num)) myMap.set(num ,num);
    if (myMap.has(num - 1)) union(num - 1, num);
    if (myMap.has(num + 1)) union(num + 1, num);// union;
  }
  
  const result = new Map();
  for (let key of myMap.keys()) {
    const keyHead = getHead(key);
    result.has(keyHead) ? result.set(keyHead, result.get(keyHead) + 1) : result.set(keyHead, 1);
  }
  return Math.max(...result.values(), 0);
};

Union Find는 여러 종류를 묶는 방법을 이해하기에는 굉장히 명료하지만 대부분의 과정에 parent를 구하는 과정이 들어있기 때문에 항상 효율적이라고 할 수 없다. 이번 문제처럼 하나의 링크에 단일 원소를 잇는 과정은 많은 반복이 필요하게 된다.

2. Set

연속된 sequence를 찾는 과정은 숫자 앞뒤의 숫자가 nums에 포함되어 있는지 찾는 과정과 같다. nums에 특정 숫자가 존재하는지 찾는 과정은 Set을 통해 O(1)의 시간복잡도를 통해 찾아낼 수 있다.

Algorithm

• nums를 Set으로 만든다.
• mySet의 원소 하나를 골라 Set에서 제거하고 앞과 뒤의 연속된 숫자가 존재한다면 또한 Set에서 제거한다.
• 연결된 sequence의 길이를 측정해 result에 반환한다.
• 위 과정을 mySet의 모든 원소가 사라질 때까지 반복한다.

var longestConsecutive = function(nums) {
  // 연이은 숫자
  // using Set
  let result = 0;
  const mySet = new Set(nums);
  for (let el of mySet) {
    let start = el;
    mySet.delete(start);
    let end = start;
    while (mySet.has(start - 1)) {
      mySet.delete(--start);
    }
    while (mySet.has(end + 1)) {
      mySet.delete(++end);
    }
    result = Math.max(result, end - start + 1);
  }
  return result;
};

Set의 has알고리즘은 해시테이블로 구성되어 이론상으론 O(1)이지만 실제 구현은 완벽하진 않다. 하지만 적어도 O(n)보다는 좋은 성능을 가지며 이를 통해 nums에서 dfs로 sequence를 찾아 효율적으로 제거할 수 있었다. 모든 원소는 Set에 추가될때 O(n) 모든 원소가 탐색되어 제거될때 O(n)로 총 O(n)의 시간복잡도를 가진다.