142. Linked List Cycle II

문제링크: https://leetcode.com/problems/linked-list-cycle-ii/description/

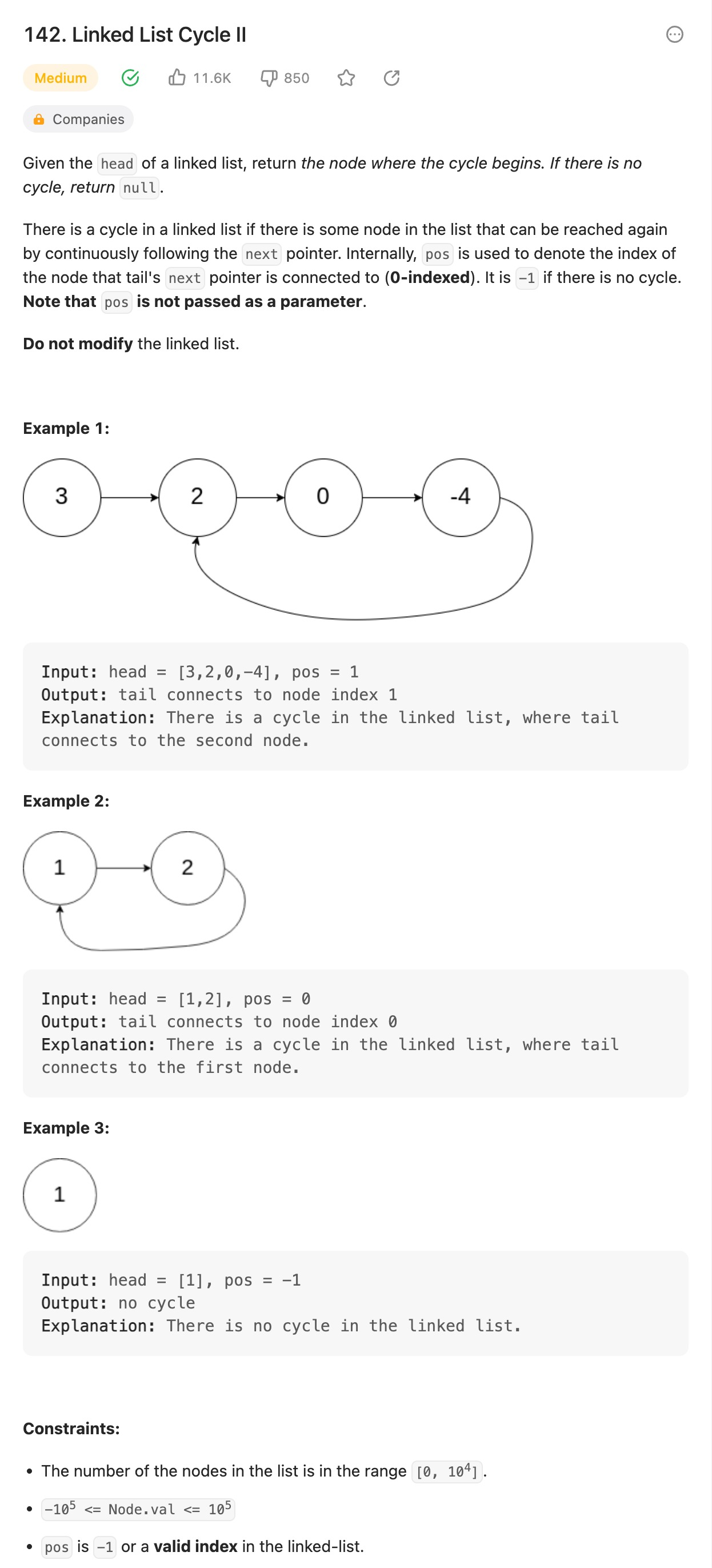
연결 리스트가 순환하는지 알아보고 순환하는 경우 순환 시작 지점을 반환하는 문제다.

Solution

Slow & Fast Pointers

리스트가 순환하는지 여부는 slow & fast pointers 로 쉽게 알 수 있다. 두 리스트씩 이동하는 fast pointer가 null을 만나기 전에 slow pointer를 만나면 순환한다. 이때 더 나아가 순환 시작 지점을 알고 싶다면 수학적인 계산이 필요하다.

순환 지점까지의 거리를 a, a부터 두 포인터가 만난 거리를 b라고 하자
slow 포인터는 a + b 만큼 이동하고 fast는 a + b + nf(공회전 거리 n, 순환주기 f)만큼 이동했다.

두 관계는 2배로 a + b는 주기(f)의 배수가 된다.

한 노드는 시작지점, 한 노드는 만난 지점에서 k 지점만큼 이동해보면
만난 노드에서 출발한 노드의 위치는 a + b + nf + k % f가 되고 처음에서 출발한 노드는 k가 된다
두지점이 만날 경우
k = a + (b + k) % f 가 되며, k 가 a일 경우 a+b는 f의 배수이기 때문에 0 이되어 같아진다.
따라서 slow와 fast노드가 만난 지점에서 시작한 노드와 처음에서 시작한 노드가 다시 이동해 만나는 지점이 순환이 시작되는 지점 a가 된다.

Alogorithm

• slow & fast 노드의 이동을 통해 순환하는지 확인하고 null을 만나면 비순환으로 반환한다.
• 만난지점을 fast, 다시 처음지점을 slow로 할당하고 한칸씩 이동한다.
• 두 노드가 다시 만난지점이 순환이 시작된 지점으로 결과를 반환한다.

Code

var detectCycle = function(head) {
  // 가장 먼저 생각나는 것: O(n) space set으로 주소들 기억하기
  /* let cur = head;
  while(cur) {
    if (nodeSet.has(cur)) return cur;
    nodeSet.add(cur);
    cur = cur.next;
  }
  return null;
  */
  // slow & fast pointer
  let slow = head, fast = head;
  while (fast && fast.next) {
    slow = slow.next;
    fast = fast.next.next;
    if (slow === fast) {
      // 순환 ok 순환지점 찾기
      slow = head;
      while(slow !== fast) {
        slow = slow.next;
        fast = fast.next;
      }
      return slow;
    }
  } 
  // a: 앞지점 b: a이후 지점까지
  // 1 : 2 = a + b : a + b + nf
  // 2a+ 2b = a + b + nf
  // a+b = nf
  // 현재지점 :  a+ b, 0, k만큼 이동
  // a + (b + k - nf) % f = k
  // a + (b + k) % f = k
  // k = a

  return null;
};

Set을 사용하면 O(n)의 공간 복잡도가 필요하지만, 포인터를 으용하여 O(n)의 시간복잡도와 O(1)의 공간복잡도로 순환 지점을 찾을 수 있었다.