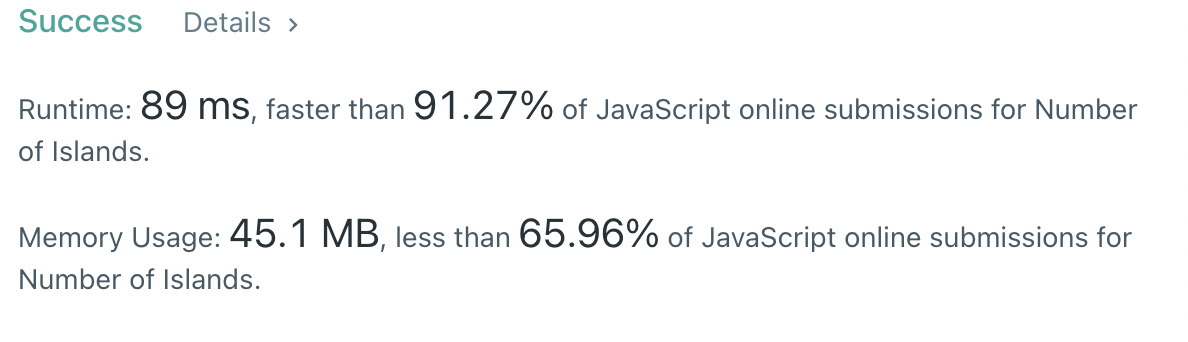
200. Number of Islands

문제링크: https://leetcode.com/problems/number-of-islands/

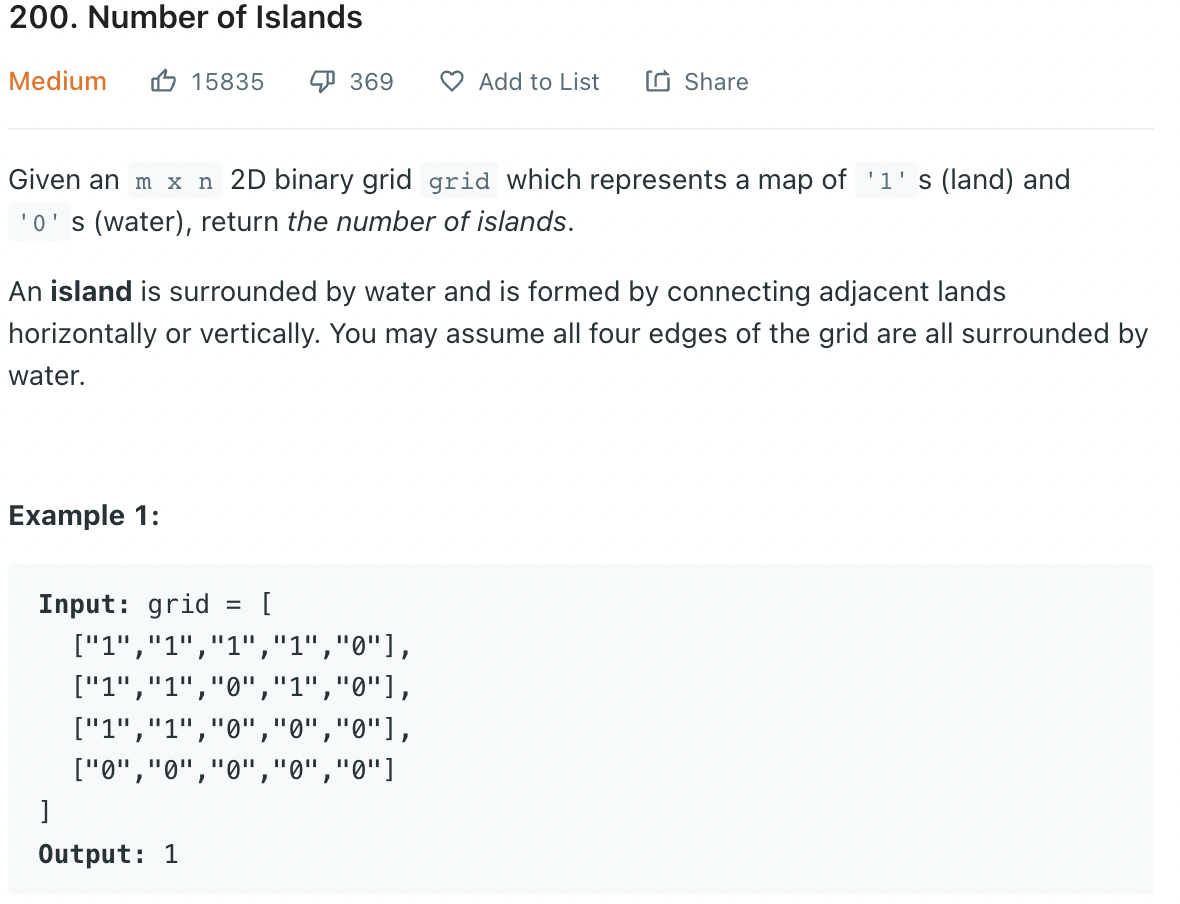
1로 표현된 땅을 기준으로 총 섬이 몇개인지 구하는 문제이다. 섬은 상하좌우가 0인 바다로 막힌 것을 섬이라 한다.

Solution

Union Find

DFS나 BFS로 풀 수도 있지만 이러한 문제를 설명하기 좋게 푸는 방법은 Union Find라고 생각했다. Union Find에 대한 설명은 다음 링크에서 볼 수 있다.
https://www.quora.com/What-is-an-intuitive-explanation-of-union-find
Union Find를 통해 땅으로 연결된 같은 지역을 하나의 parent로 수렴할 수 있도록 묶는다면 전체 parent의 수를 통해 섬이 몇개인지 알아낼 수 있다.

Algorithm

• Union이라는 객체를 만들어 grid의 땅들이 각자 스스로를 부모로 갖도록 한다.
• 각 땅을 탐색하면서 상하좌우의 인접한 땅을 Union.union을 통해 같은 부모로 묶는다.
• 각 지역은 이제 인접한 땅인 경우 같은 조상을 가지게 된다.
• 해당 조상의 수를 세서 섬의 개수를 파악할 수 있다.

var numIslands = function(grid) {
    const m = grid.length, n = grid[0].length;
    const isValid = (x, y) => {
        if (x < 0 || x >= m || y < 0 || y >= n) return false;
        return grid[x][y] === '1'
    }
    
    //union?
    const myUnion = new Union(grid);
    // row로 한번, col로 한번
    const upDownLeftRight = [0, -1, 0, 1, 0]
    
    for (let i = 0; i < m; i++) {
        for (let j = 0; j < n; j++) {
            if (isValid(i, j)){
                // console.log(hi);
                for (let k = 0; k < 4; k++) {
                    if (isValid(i + upDownLeftRight[k], j + upDownLeftRight[k + 1])) {
                        myUnion.union([i, j], [i + upDownLeftRight[k], j + upDownLeftRight[k + 1]]);
                    }
                }
            }
            
        }
    }
    
    const resultCount = new Set();
    myUnion.unionArr.forEach((row) => row.forEach((el) => {
        if (typeof el === 'object') resultCount.add(myUnion.parent(el).toString());
    }));
    return resultCount.size;
};

function isArraysEqual(a, b) {
  if (a === b) return true;
  if (a == null || b == null) return false;
  if (a.length !== b.length) return false;

  for (var i = 0; i < a.length; ++i) {
    if (a[i] !== b[i]) return false;
  }
  return true;
}

class Union {
    constructor(grid) {
        this.unionArr = grid.map((row, idx1) => row.map((col, idx2) => {
            return col === '1' ? [idx1, idx2] : 0;
        }));
    }
    
    parent([x, y]) {
        while (!isArraysEqual(this.unionArr[x][y], [x, y])) {
            [x, y] = this.unionArr[x][y];
        }
        // console.log('parent:', [x, y]);
        return [x,y];
    }
    
    union([x1, y1], [x2, y2]) {
        const pa1 = this.parent([x1, y1]);
        const pa2 = this.parent([x2, y2]);
        if (isArraysEqual(pa1, pa2)) return;
        const [a, b] = pa1;
        this.unionArr[a][b] = pa2;
    }
}

O(m*n)의 시간 복잡도를 가지고 있는데 이중배열을 처음 union으로 표현 해보니 각 부모를 표현하고 비교하는데 isArraysEqual이라는 함수를 만들어 썼다. 그런데 이 과정이 모든 비교, 부모호출 과정에 들어가게 되다 보니 복잡도 자체는 문제가 없지만 개별 과정에 큰 시간이 소요되었다. 좌표를 ${x}_${y}방식으로 인코딩해 하는 방식도 괜찮아보인다.

DFS

Union에서 좌표를 encode하고 비교하는 시간이 굉장히 많이 걸렸기 때문에 그냥 좌표 그대로의 성질을 사용하기 위해 DFS로 가볍게 구현해보았다. 새로운 1지점을 탐색할 때 resultCount를 증가시켜 새로이 탐색을 시작하고 한번에 인접한 땅을 모두 탐색한다. 이 때, 이미 탐색한 땅을 바다로 바꿔서 다시 탐색하지 않도록 했다.

Algorithm

• grid를 탐색하면서 새 땅을 발견한다.
• 새 땅이 발견되면 resultCount를 1 증가시키고 인접 지역을 모두 탐색하는 dfs 재귀를 시작한다.
• 탐색한 지역은 0으로 바꿔 다시 탐색하지 않도록 한다.
• 모두 탐색한 후에 resultCount를 반환한다.

var numIslands = function(grid) {
    // dfs
    const m = grid.length;
    const n = grid[0].length;
    const isValid = (x, y) => {
        if (x < 0 || x >= m || y < 0 || y >= n) return false;
        if (grid[x][y] !== '1') return false;
        return true;
    };
    
        
    let resultCount = 0;
    const searchWay = [0, -1, 0, 1, 0];
        
    const dfsSearch = (x, y) => {
        if (!isValid(x, y)) return;
        grid[x][y] = '0'; // same as hasBeen
        for (let k = 0; k < 4; k++) {
            if (isValid(x + searchWay[k], y + searchWay[k + 1])) {
                dfsSearch(x + searchWay[k], y + searchWay[k + 1]);
            }
        }
    }
        
    for (let i = 0; i < m; i++) {
        for (let j = 0; j< n; j++) {
            if (isValid(i, j)) {
                // 새 섬 탐색 시작
                resultCount++;
                dfsSearch(i, j);
            }
        }
    }
    return resultCount;
};