235. Lowest Common Ancestor of a Binary Search Tree

문제링크: https://leetcode.com/problems/lowest-common-ancestor-of-a-binary-search-tree/

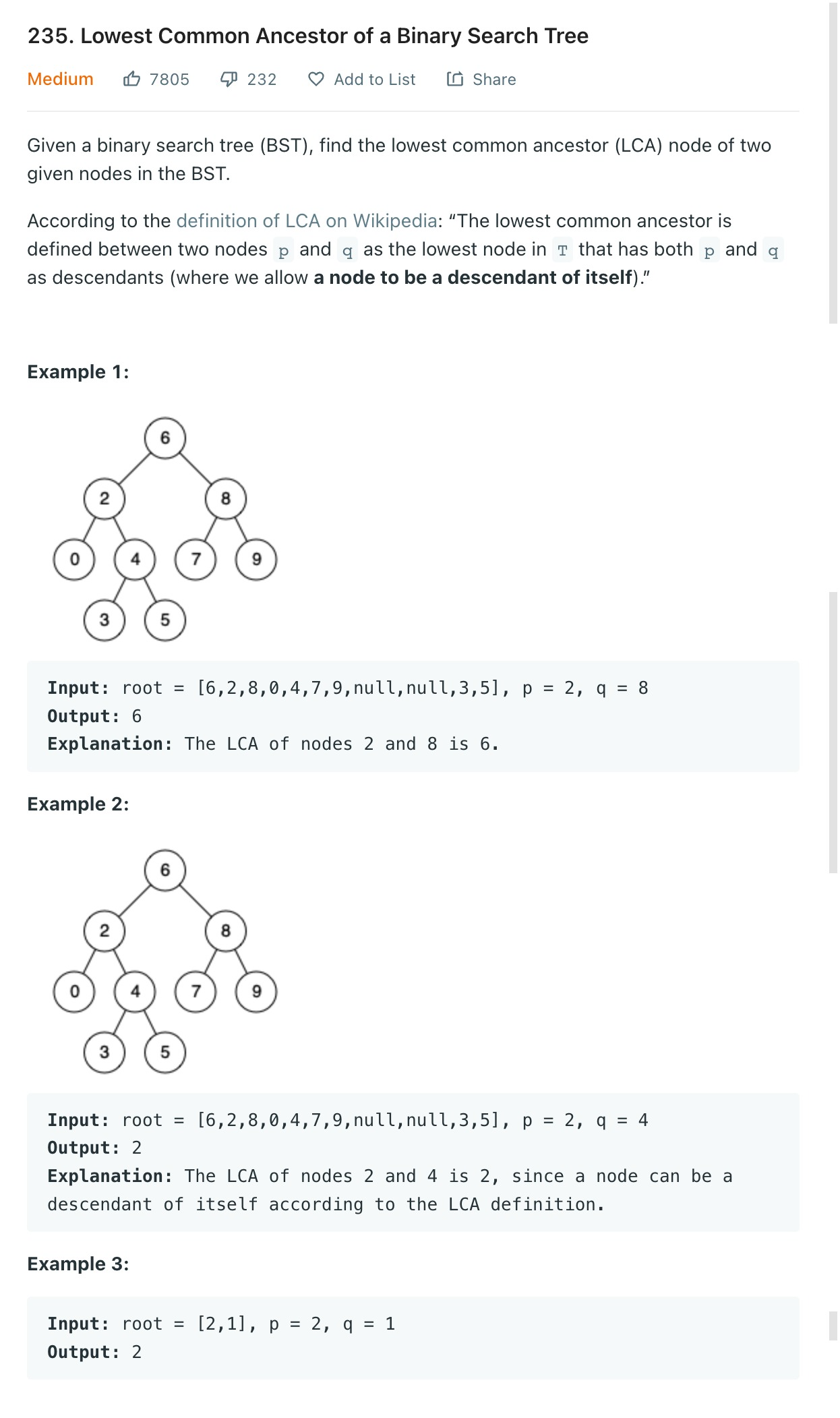
중복 없는 BST에서 두 원소의 공통조상을 찾는 문제다.

Solution

1. DFS

두 원소를 찾을 때 까지 탐색한 후 두 노드의 노드 ~ 루트의 관계를 저장해 두 원소의 공통 부모를 찾을 수 있다. 이 방식은 BST가 아니더라도 사용할 수 있다.

Algorithm

• DFS를 통해 두 노드 모두가 탐색 될 때까지 탐색한다. (O(n) time)
• 탐색할 때 루트 ~ 현재노드 까지의 path를 동시에 저장하고 (O(logn) space) 원하는 노드일 경우 따로 저장한다.
• 위 과정을 통해 두 노드의 노드 ~ 부모 간의 path정보를 알 수 있고 하나를 Set으로 변환하고 하나는 뒤에서 부터 Set에 포함되어 있는지 확인해 가장 아래의 공통 조상을 찾을 수 있다.

var lowestCommonAncestor = function(root, p, q) {
  // 두 개의 위치를 찾아야함
  // 지정노드에서 부모로가는 루트를 저장한다.
  // ex) p : [1,2,3,4]
  // q: [1,5,6,7]
  // 공통조상을 찾는다.
  let pPath = [];
  let qPath = [];
  const path = [];
  const dfs = (root) => {
    if (!root) return;
    
    if (pPath.length && qPath.length) return;
    path.push(root);
    // console.log(root.val, path);
    if (root === p) pPath = path.slice(0);
    if (root === q) qPath = path.slice(0);
    dfs(root.left);
    dfs(root.right);
    path.pop();
  }
  dfs(root);
  // console.log(pPath, qPath);
  const pathSet = new Set(pPath);
  for (let el of qPath.reverse()) {
    if (pathSet.has(el)) return el;
  }
};

DFS의 모든 노드를 탐색하기 때문에 O(n) 의 시간 복잡도를 가진다. BST의 성질을 전혀 사용하지 않았기 때문에 성질을 이용한 좋은 방법을 찾아보기로 했다.

2. BST recursive

BST에서 a가 최하단의 공통 조상인 경우 p.val <= a.val <= q.val의 형태로 나타나는 최초의 노드다. 즉 root로 부터 탐색을 시작해 최초로 위의 수식을 만족하는 노드가 바로 LCA가 된다.

Algorithm

• 공통조상을 찾기 위해 root노드부터 시작해 현재 노드값이 목표 노드의 중간값인지 확인한다.
• 중간값일 경우 현재 노드가 결과가 된다.

var lowestCommonAncestor = function(root, p, q) {
  // bst에서 찾는 방법
  // 현재 노드가 중간값일 경우 => 공통조상
  // 중간값이 아니라 치우쳐 있을 경우 가까운 노드 탐색
  let result;
  const bst = (root) => {
    if ((root.val - p.val) * (root.val - q.val) <= 0) {
      // 중간값이거나 같은 값일 때
      result = root;
      return;
    }
    else if (root.val - p.val > 0) return bst(root.left);
    else return bst(root.right);
  }
  bst(root);
  return result;
};

공통 조상을 탐색하는 과정은 모든 노드를 탐색하지 않고도 BST의 성질을 사용해 O(logn)의 시간복잡도로 찾을 수 있다.