62. Unique Paths

문제링크: https://leetcode.com/problems/unique-paths/

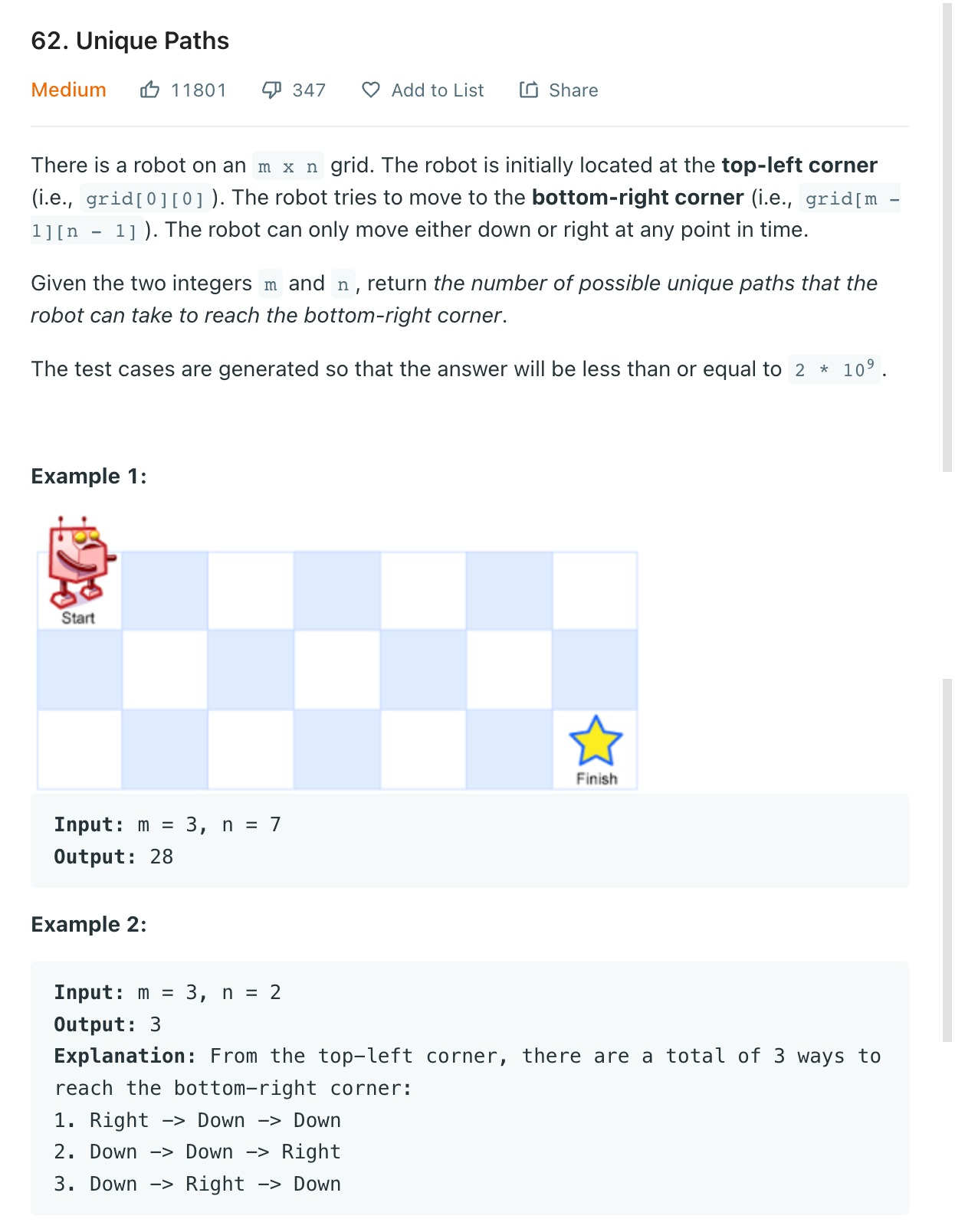
우측 아래의 목표로 최단거리로 가는 방법의 경우의 수를 구한다.

Solution

Combination

최단거리로 가기 위해서는 오른쪽과 아래방향으로만 갈 수 있다. 이 때 오른쪽의 횟수와 아래 횟수는 정해져 있고 이들의 순서를 바꾼다면 다를 방법이된다. 따라서 오른쪽과 아래 방향의 순서를 바꾸는 방법의 경우의 수를 조합으로 구할 수 있다.

(m + n - 2) Combination(n - 1) = (m+ n - 2)! / (m - 1)!(n - 1)!

Algorithm

• (m + n - 2)! / (m - 1)! 은 m ~ m + n - 2까지의 곱으로 구할 수 있다.
• 이후 위의 결과를 (n - 1)!으로 나누면 결과를 도출할 수 있다.

var uniquePaths = function(m, n) {
  // 수학적으로 풀어보기
  // m - 1: 아래로 가는 횟수
  // n - 1: 오른쪽으로 가는 횟수
  // (m + n - 2) C (n - 1);
  // (m + n - 2)! / (n-1)! * (m - 1)!
  const numerator = m + n - 2;
  const denom1 = n - 1;
  const denom2 = m - 1;
  let result = 1;
  for (let i = denom1 + 1; i <= numerator; i++) {
    result *= i;
  }
  for (let i = 1; i <= denom2; i++) {
    result /= i;
  }
  return result;
};