64. Minimum Path Sum
문제링크:https://leetcode.com/problems/minimum-path-sum/
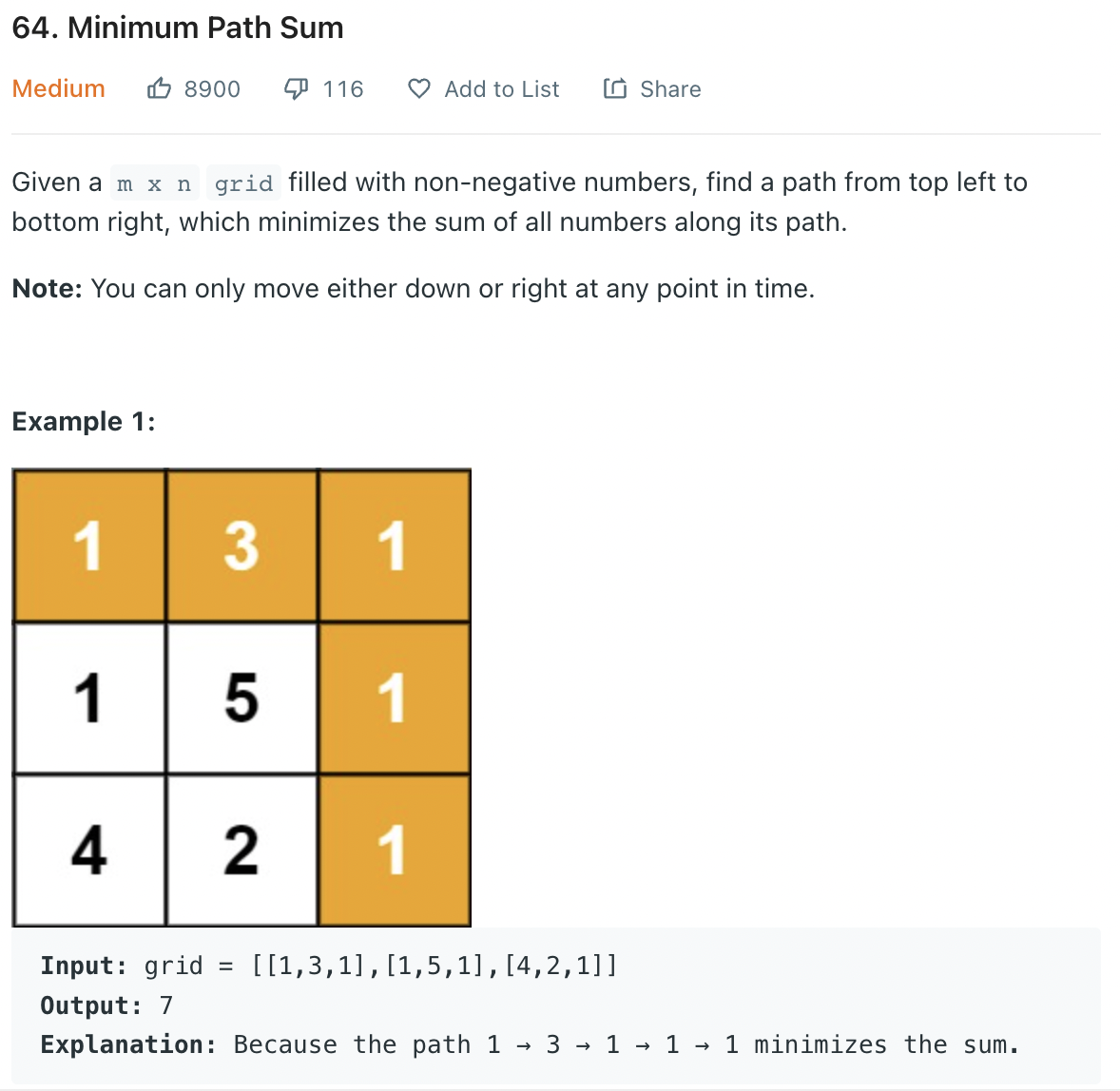
첫번째 칸에서 마지막 칸까지 오른쪽 또는 아래로 움직여서 지나가는 숫자들의 최소합을 구하는 문제다.
Solution
1. Dynamic programming O(n) space
이동 방향이 오른쪽과 아래방향 밖에 없기 때문에 어떤 블럭 grid[i][j]에 도달하기 위해선 grid[i-1][j]와 grid[i][j-1]에서만 올 수 있고, 이는 둘중 작은 값을 통해서 접근하는게 최소값이 된다. 따라서 이전 row를 저장해 grid[i-1][j]를 통해 얻고 바로 전 값을 통해 grid[i][j-1]을 얻는 DP로 구현할 수 있다.
Algorithm
memPrev는 이전row로 맨 첫번째row는 앞에 값을 더하면서 구한다.i,j를 통해 나머지 공간을 반복한다.- 현재값을
grid[i][j-1]에 도달값인memCur[j-1]과grid[i-1][j]도달값인memPrev[j]를 비교해 작은 값으로 계산해 얻는다. - 모든 반복이 끝나고 남은 마지막
row인memPrev에서 가장 마지막 값memPrev[cLen - 1]을 반환한다.
var minPathSum = function(grid) {
// DP: 왼쪽에서 오는법, 위에서 오는 법 둘 중 하나만 가능하기 때문에 둘을 비교 해서 진행
let temp = 0;
let memPrev = grid[0].map((el) => {
temp += el;
return temp;
});
const rLen = grid.length;
const cLen = grid[0].length;
for (let i = 1; i < rLen; i++) {
const memCur = [memPrev[0] + grid[i][0]];
for (let j = 1; j < cLen; j++) {
memCur[j] = grid[i][j] + Math.min(memCur[j-1], memPrev[j]);
}
memPrev = memCur;
}
return memPrev[cLen - 1];
};
i, j 를 통해 시간복잡도 O(mn), memPrev에서 생긴 공간복잡도 O(n) 을 가진다.
2. Dijkstra (not recommended)
다익스트라 알고리즘의 경우 간선에 따라 시간복잡도가 O(MNlogMN)에 달하기 때문에 위의 방식으로 전체 matrix를 한번 순회하는 것으로 얻을 수 있는 문제는 구현도 쉽지않고 효율적이지도 못하다. 하지만 여기서도 구현할 수 있는지 확인해보기 위해 한번 시도해보았다.
우선순위 큐를 제외하고 배열 좌표를 r * cLen + c로 인코딩해 새 배열에 할당하고 다익스트라 알고리즘을 적용했다.
Algorithm
dj는 거리를 저장하는 배열,shortest는 최단거리를 구했는지 여부를 판단하는 배열이다.- while문을 통해 마지막배열
shortest[end]를 구했는지 확인하고 구할 때까지 반복한다. shortest가false인 부분 중 가장 작은 곳을 찾는다.- 해당부분은
shortest가true가 되고 갈 수 있는 곳(오른쪽과 아래쪽)좌표를 구해 그곳의 최단거리를 갱신한다. - 마지막 값을 구하면 결과를 반환한다.
var minPathSum = function(grid) {
// 다익스트라? 방향 오른쪽 or 아래로만 이동 가능
// 다익스트라: 목표지점에 갈 수 있는 방법이 최소일 때까지 가장 가까운 곳을 더 탐색하는 방식
const rLen = grid.length;
const cLen = grid[0].length;
const getGridNum = (n) => {
return grid[parseInt(n / cLen)][n % cLen];
}
const end = rLen * cLen - 1;
const dj = new Array(end + 1).fill(Infinity);
const shortest = new Array(end + 1).fill(false);
dj[0] = grid[0][0];
while (!shortest[end]) {
// shortest false 중에 가장 작은 곳 구함
let min = Infinity;
let minIdx;
for (let i = 0; i <= end; i++) {
if (!shortest[i] && dj[i] < min) {
min = dj[i];
minIdx = i;
}
}
// 현재노드 shortest true
shortest[minIdx] = true;
// 해당 노드에서 갈 수 있는 다음 노드들 계산
// 오른쪽
if ((minIdx + 1) % cLen !== 0) {
dj[minIdx + 1] = Math.min(dj[minIdx] + getGridNum(minIdx + 1),dj[minIdx + 1]);
}
// 아래쪽
if ((minIdx + cLen) <= end) {
dj[minIdx + cLen] = Math.min(dj[minIdx] + getGridNum(minIdx + cLen),dj[minIdx + cLen]);
}
}
return dj[end];
};
matrix로 주어진 문제는 이미 노드간 연결이 규칙적으로 되어있기 때문에 배열 탐색을 통해 쉽게 구할 수 있는 경우는 더 복잡한 알고리즘을 사용할 필요가 없다. 또한 현재 우선순위큐가 구현이 안되었기 때문에 최단거리인 부분을 찾을 때 항상 O(mn)의 시간 복잡도가 걸렸고 이는 큰 matrix일 수록 시간복잡도가 크게 증가하는 문제가 있다. 또한 1번은 reduced DP로 memoization에 필요한 공간을 O(n)으로 감소시켰지만 이 방식은 모든 노드에 대해 거리를 저장하기 위해 O(mn)의 복잡도를 필요로했다.

