96. Unique Binary Search Trees

문제링크: https://leetcode.com/problems/unique-binary-search-trees/

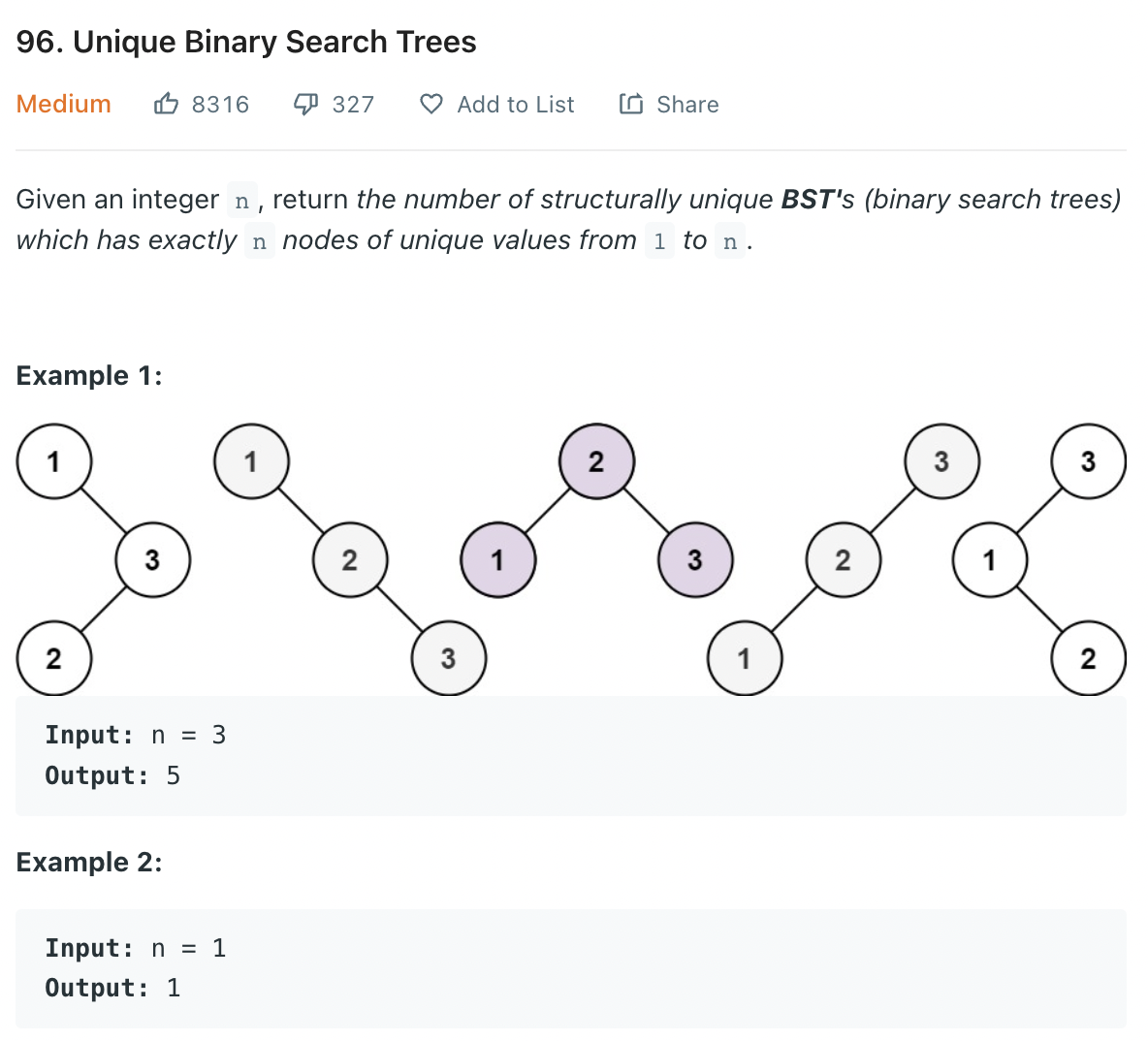
1~n의 값을가지는 BST의 종류 개수를 구하는 문제다.

Solution

BST 는 트리 모양이 정해지면 단 하나의 방법으로만 값이 존재할 수 있다.

Dynamic programming

수학적으로 접근할 수 있을것처럼 보였다. 처음엔 계차수열로 접근하려 했으나 계차가 등차보다 빠르게 커지는 것을 보고 관계는 있다고 판단했다. 하지만 계차수열은 아니기에 다른방법을 생각해보았다.

3번째 예시 결과를 보면 루트를 하나 정해놓고 왼쪽 방향으로 2개의 방법, 오른쪽 방향으로 2개의방법, 양쪽으로 하나씩 놓는 방법으로 총 5가지의 방법이 있다. 3번째에서는 좌우로 2개씩의 방법과 양쪽으로 뻗는 방법을 추론할 수 있다. 그렇다면 4번째도 같은 방법으로 접근하면 좌우로만 뻗는 방법 P(3) * 2 과 양쪽으로 뻗는 방법으로 왼쪽에 1개, 오른쪽에 2개 또는 왼쪽에 2개 오른쪽에 1개인 방법이 있다. 여기서 점화식을 얻을 수 있었다.

P(n) = P(n-1)*P(0) + P(n-2)*P(1) + P(n-3)*P(2) + ... + P(0)*P(n-1)

루트하나를 기준으로 좌로 뻗는개수와 우로 뻗는 개수를 정하면 이는 앞에서 사용한 데이터를 이용해 얻을 수 있고 이 둘을 곱하면 경우의 수가 된다. 루트 노드를 빼고 좌로 뻗는 개수는 최대 n-1개에서 0개가 되고 우로 뻗는 개수는 반대로 0개에서 n-1로 얻을 수 있다. 이 방법을 DP를 이용해 구현해볼 수 있었다.

Algorithm

• mem 을 통해 동적프로그래밍을 구현한다. mem[0]는 1이다.
• 재귀적으로 값을 얻을 수도 있지만 어차피 1부터 n까지의 모든 연산 값이 필요하기 때문에 iteration을 통해 mem을 채운다.
• mem[i]를 구하기 위해서 j를 1 ~ i까지 반복해 더한다.
• 위 방법으로 mem[n]까지 구한 후 mem[n]을 반환한다.

var numTrees = function(n) {
  // 수식으로 접근
  // P(0) = 1
  // P(1) = 1
  // P(2) = 2
  // P(3) = 5
  // P(4) = 10 + 4 = 14
  // P(n) = P(n-1) * P(0) + P(n-2) * P(1) + P(n-3) * P(2) + ... P(0) * P(n-1);
  // DP
  const mem = [1];
  for (let i = 1; i <= n; i++) {
    mem[i] = 0;
    for (let j = 1; j <= i; j++) {
      mem[i] += mem[i - j] * mem[j - 1];
    }
  }
  return mem[n];
};