858.Mirror Reflection

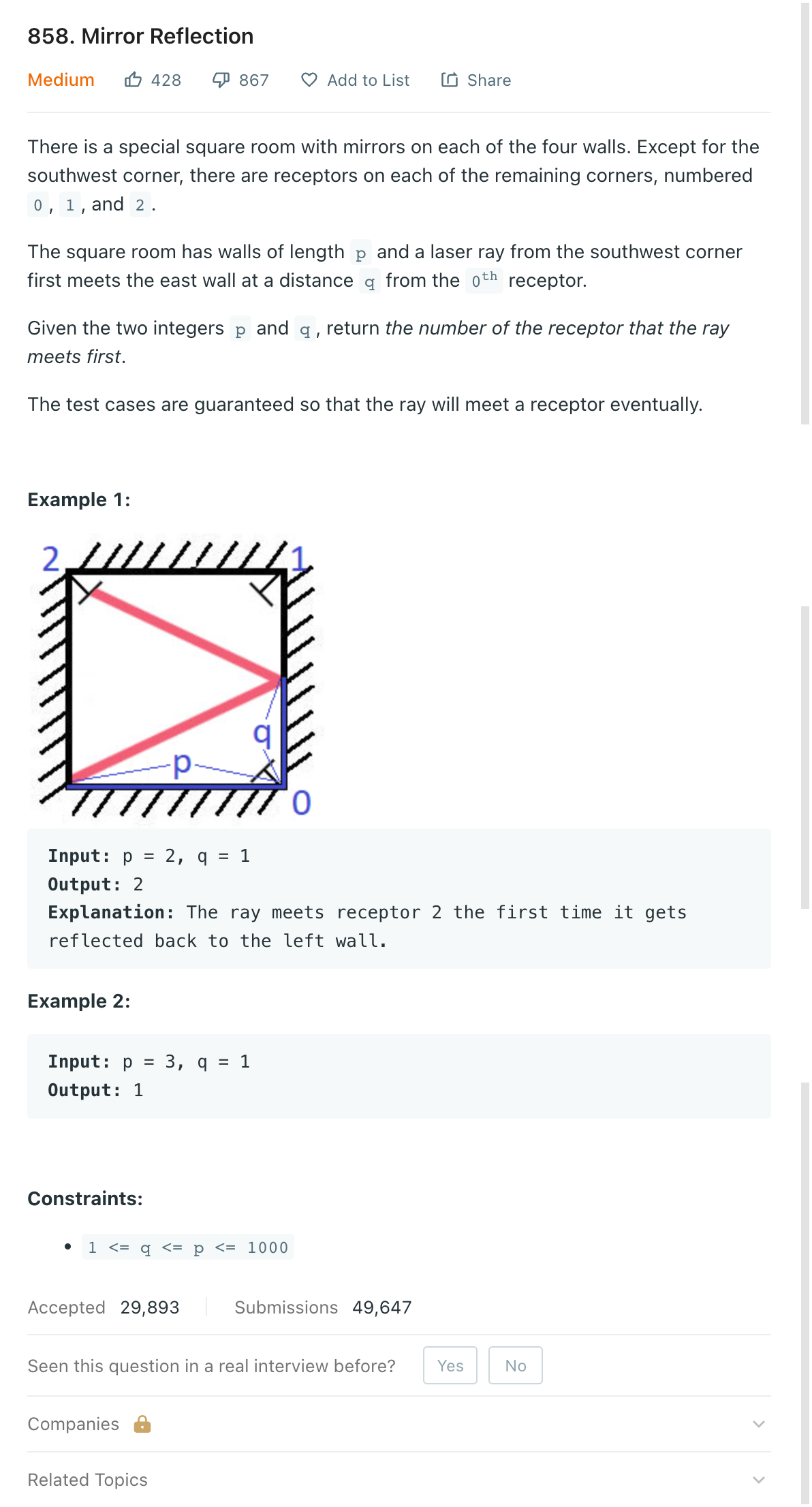
문제 링크: https://leetcode.com/problems/mirror-reflection/

Solution

iteration으로 접근

매번 튕기는 위치를 구할 수 있다. (이전에 튕긴 위치, 레이저의 방향(위 or 아래)
튕기는 위치는 결국 모서리에 접근하기 위해 p의 배수가 되는 y축 지점에 도달한다.
따라서 최종 모서리의 위치는 수학적으로 접근해 모서리 위치를 구할 수 있다.

수학적으로 접근

p 와 q의 최소공배수가 되는 지점이 모서리에 도달하는 경우다.

• 모서리에 접근하기 위해서는 q * (튕긴 횟수) 가 p의 배수가 되어야 한다.
• 이는 p와 q의 최소공배수로 (최소공배수) / q 가 튕긴 횟수가 된다.

튕긴 횟수 (좌, 우에 튕긴 경우만 고려)에 따라 모서리 위치가 결정된다.

• 짝수번 튕긴 경우 : 2 또는 시작위치, 하지만 조건에 시작위치로 가는 경우는 없다고 했기 때문에 2에 도착한다.
• 홀수번 튕긴 경우 : 1 또는 0 에 도착하며 1과 0의 판단은 (최소공배수) / q 의 값으로 결정된다. (홀수일 경우 1, 짝수일 경우 0)

var mirrorReflection = function(p, q) {
    let reflectCount;
    for (let i = 1; i <= p; i++) {
        if (i * q % p === 0) {
            reflectCount = i;
            break;
        }
    }
    if (reflectCount % 2 === 0) return 2;
    else if ((reflectCount * q) % (p * 2) === 0) return 0;
    else return 1;
};

개선사항

• 최소공배수를 구하는 과정을 최적화
• 최소공배수를 구하기 전에 찾을 수 있는 결과들을 먼저 도출하기