2-3 Tree는 트리의 높이가 균형을 이루며 내부노드의 차수가 2 또는 3인 균형 탐색 트리이다.
Tree는 Inter Node와 External Node의 개념이 존재한다.
Internal Node는 key가 들어있는 내부 노드이며,
External Node는 데이터가 들어있지 않은 노드로써 Internal Node의 Leaf Node의 자식으로 존재하는 가상의 노드이다.
무슨 말인가하면,
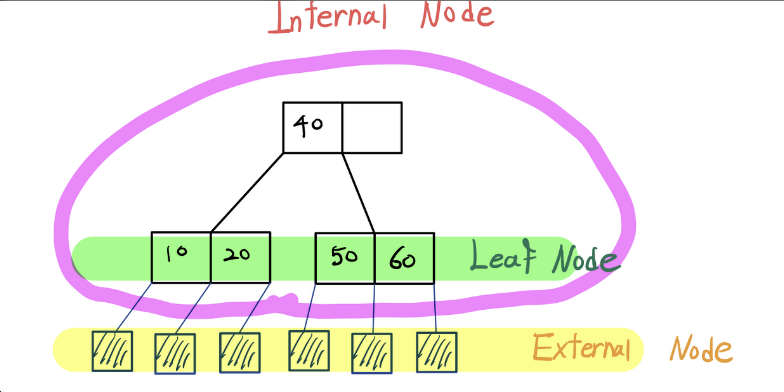
이런식으로 생겼다.
특이하게도 각 노드의 값의 크기 순서는 다음과 같다.
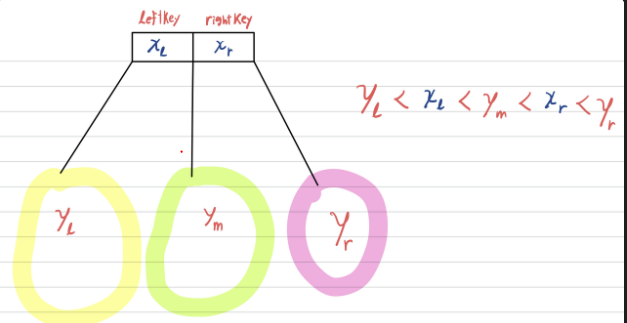
검색
검색은 BST처럼 크기 순서대로 탐색하면 된다.
leftKey 보다 작으면 leftSubTree를 찾고
leftKey 보다 크고 rightKey보다 작으면 middleSubTree를 찾는다
rightKey보다 크면 rightSubTree를 탐색한다.
삽입
삽입은 무조건 leaf Node에 삽입한다. 부모노드 에는 삽입하지 않는다.
leaf Node에 용량이 꽉차지 않았다면 순서에 따라 삽입하면 된다.
만약, 용량이 꽉찼다면 분할을 수행해야 한다.
분할 과정은 다음과 같다.
1. 추가될 데이터를 포함하여 중앙값을 결정한다.
2. 중앙값을 부모노드에 추가시키며 중앙값보다 작은 값들은 왼쪽 서브트리, 중앙값보다 큰 값들은 오른쪽 서브트리가 된다.
3.부모 노드가 없다면 새로 생성하며, 부모노드에서도 용량이 가득찼다면 똑같이 분할 과정을 반복한다.
예시를 살펴보자.
-
초기상태
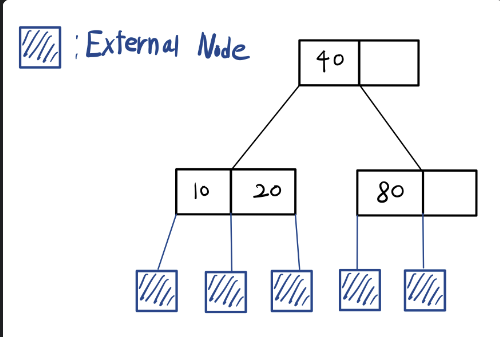
-
70삽입
무조건 leaf node에 삽입
삽입했을때, leftKey가 rightKey보다 크다면 바꾸어준다.
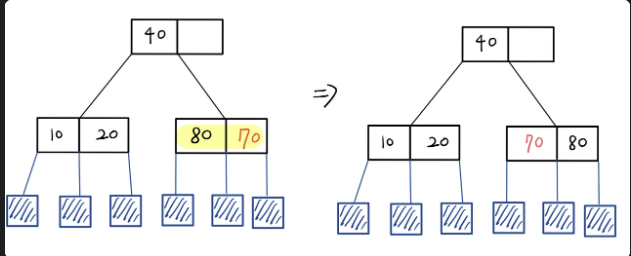
-
30삽입
30을 삽입했더니, Node가 꽉찼다. 따라서 꽉찬 노드의 중앙값을 split해준다. split해주고 나서는 External Node의 Level이 다름을 알 수 있다. Level은 무조건 같아야하므로 20을 부모노드의 값으로 올려준다.
삭제
삭제에는 Rotation과 Merge의 개념이 사용된다.
주의 해야 할것은 항상 keynode 보다 1더 많은 수의 subnode를 가진다는 것이다. 예를들어 부모노드가 1개이면 서브노드는 2개여야 하고, 부모노드가 2개이면 서브노드는 3개여야 한다!!
그림으로 살펴보는게 이해하기 쉽다.
Rotation
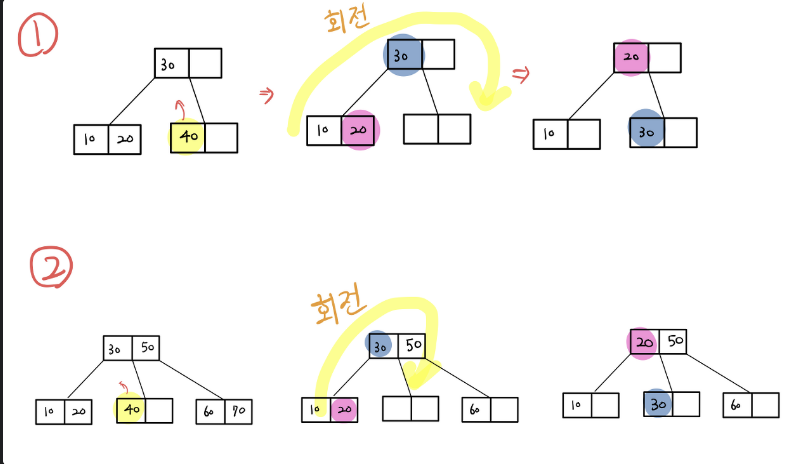
1번 그림에서 원소 40이 삭제되었다. 형제노드인 20이 부모노드로 이동하고 부모노드인 30이 삭제된 원소의 위치로 이동한다. 이걸 rotation한다고 한다.
2번 그림에서 원소 40이 삭제되었다. 형제노드인 20이 부모노드로 이동하고 부모노드인 30이 삭제된 원소 자리로 이동하였다.
rotation은 삭제 노드의 형제노드가 3-Node일때 가능하다.
Merge
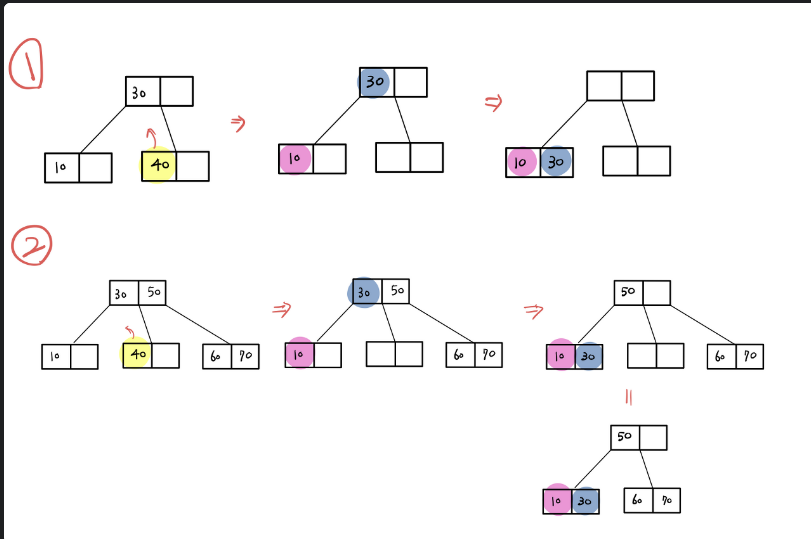
Merge는 삭제 노드의 형제노드가 2-Node일때 가능하다.
40을 삭제한후, 부모노드를 2-노드인 형제노드로 이동시켜 병합해준다.
